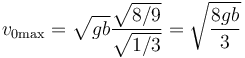Partícula girando suspendida de un hilo
De Laplace
| Línea 63: | Línea 63: | ||
<center><math>v_0=\sqrt{\frac{F_Tb}{m}}\cos(\theta)=\sqrt{gb}\frac{\cos(\theta)}{\sqrt{\mathrm{sen}(\theta)}}</math></center> | <center><math>v_0=\sqrt{\frac{F_Tb}{m}}\cos(\theta)=\sqrt{gb}\frac{\cos(\theta)}{\sqrt{\mathrm{sen}(\theta)}}</math></center> | ||
| + | |||
| + | Siu la tensión máxima vale 3mg, entonces el seno del ángulo debe cumplir | ||
| + | |||
| + | <center><math>3mg \geq \frac{mg}{\mathrm{sen}(\theta)}\qquad\Rightarrow\qquad \mathrm{sen}(\theta)\geq \frac{1}{3}</math></center> | ||
| + | |||
| + | siendo el valor máximo de la rapidez el correspondiente a que el seno valga 1/3, es decir | ||
| + | |||
| + | <center><math>v_{0\mathrm{max}} = \sqrt{gb}\frac{\sqrt{8/9}}{\sqrt{1/3}}=\sqrt{\frac{8gb}{3}}</math></center> | ||
==Energía mecánica== | ==Energía mecánica== | ||
==Momento cinético== | ==Momento cinético== | ||
Revisión de 22:22 12 sep 2016
Contenido |
1 Enunciado
Una partícula de masa m gira horizontalmente con rapidez v0, atada a un hilo inextensible y sin masa de longitud b. El hilo forma un ángulo constante θ con la vertical. En t = 0 la partícula se encuentra en el plano OXZ, según los ejes indicados en la figura.

- Exprese las ecuaciones horarias del movimiento: x(t), y(t) y z(t).
- Calcule el valor de v0 así como la tensión del hilo, en función del ángulo θ (y m, g y b). Si el hilo soporta una tensión máxima Fmax = 3mg, que si se supera se rompe, ¿cuál es la rapidez máxima que le podemos comunicar a la masa sin que se rompa el hilo?
- Calcule la energía mecánica de la partícula como función de θ (y m, g y b, pero no v0). Tómese como origen de energía potencial el punto O de anclaje del hilo
- Calcule el momento cinético de la partícula respecto al punto O como función de θ y del tiempo (y m, g y b, pero no v0). ¿Es constante alguna de sus componentes?
2 Ecuaciones horarias
La partícula tiene una altura constante, ya que gira horizontalmente

Su movimiento es circular, siendo el radio de la circunferencia
La partícula se mueve con rapidez constante v0 por lo que su periodo de revolución sale de
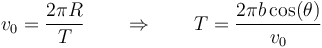
y por tanto la velocidad angular vale
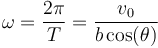
lo que nos da las ecuaciones horarias restantes

3 Velocidad y tensión
Esta parte es casi idéntica a otro problema ya resuelto.
La partícula descrive un movimiento circular uniforme, por lo que su aceleración será puramente normal y hacia adentro de la circunferencia. Empleando coordenadas cilíndricas
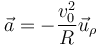
Esta aceleración es causada por la superposición de dos fuerzas:
- El peso
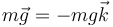
- La tensión del hilo, dirigida a lo largo de éste

Llevando esto a la segunda ley de Newton
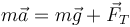
queda, por componentes
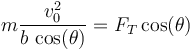
y

De aquí obtenemos la tensión

y la rapidez de la partícula

Siu la tensión máxima vale 3mg, entonces el seno del ángulo debe cumplir

siendo el valor máximo de la rapidez el correspondiente a que el seno valga 1/3, es decir