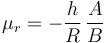Esfera que rueda por un carril
De Laplace
m |
|||
| Línea 112: | Línea 112: | ||
<center><math>mg\,\mathrm{sen}(\beta) \frac{\gamma R^2}{2(h^2+R^2\gamma)}\leq \mu_s \frac{mgR\cos(\beta)}{2h}</math></center> | <center><math>mg\,\mathrm{sen}(\beta) \frac{\gamma R^2}{2(h^2+R^2\gamma)}\leq \mu_s \frac{mgR\cos(\beta)}{2h}</math></center> | ||
| - | que, en términos del ángulo queda | + | que, en términos del ángulo, queda |
| - | <center><math>\mathrm{tg}(beta) \leq \mu_s \frac{(h^2+R^2\gamma)}{\gamma R h}</math></center> | + | <center><math>\mathrm{tg}(\beta) \leq \mu_s \frac{(h^2+R^2\gamma)}{\gamma R h}</math></center> |
==Con rozamiento por rodadura== | ==Con rozamiento por rodadura== | ||
Revisión de 09:51 18 jun 2016
1 Enunciado
En los experimentos de Galileo, éste hizo rodar una esfera de radio R por un carril de anchura 2b (b < R), de forma que la bola rueda apoyada en los bordes del carril, minimizando el rozamiento.
El carril se encuentra inclinado un ángulo β respecto a la horizontal.
La bola posee masa m y un momento de inercia I = γmR2 (con γ entre 2/5, esfera maciza y 2/3, esfera hueca).
Suponiendo que las fuerzas a ambos lados del carril son simétricas, determine la aceleración con la que la bola desciende por el carril, si inicialmente se encuentra en reposo.
Determine el ángulo β máximo para el carril si no se desea que la bola deslice.
Supóngase ahora que existe un rozamiento por rodadura de forma que en los puntos de contacto se ejerce una fuerza adicional 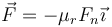 , siendo el eje X el tangente al carril en la dirección de avance. ¿Cuál es en ese caso la aceleración de la bola?
, siendo el eje X el tangente al carril en la dirección de avance. ¿Cuál es en ese caso la aceleración de la bola?
2 Caso sin rozamiento
Tomaremos un sistema de ejes en el que OX es el eje tangente al plano inclinado, OY el normal a él en el plano de movimiento y OZ el ortogonal a ambos hacia afuera del plano.
La esfera se encuentra sometida a una serie de fuerzas:
- Su peso
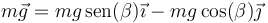
- Las fuerzas normales en los puntos de contacto A y B. Estas fuerzas son normales a la superficie de la esfera y por tanto son radiales.
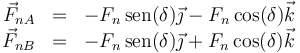
- por simetría, las dos reacciones tienen el mismo módulo y direcciones simétricas. \delta es el ángulo que el vector radial forma con la superficie del plano. Este águlo verifica
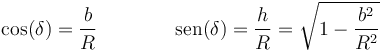
- Las fuerzas de tangenciales en los puntos de contacto. De nuevo por simetría, ambas son iguales. Estas fuerzas son de rozamiento estático, ya que la velocidad en los puntos de contacto es nula
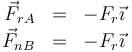
- para que no haya deslizamiento, estas fuerzas deben cumplir
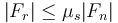
de manera que la aceleración del CM cumple la ecuación
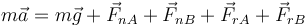
Separando en componentes
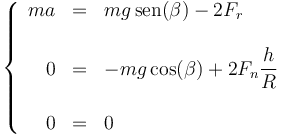
Esto nos permite hallar el módulo de la fuerza normal
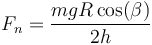
pero aun no la aceleración, ya que tenemos dos incógnitas: la propia aceleración y el valor de la fuerza tangencial.
Para completar el sistema necesitamos la ecuación para la rotación del sólido
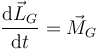
Por tratarse de una esfera, el momento cinético es proporcional a la velocidad angular
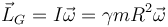
La velocidad angular, por su parte, va en una dirección paralela a la recta que pasa por A y B (ya que estos dos puntos están en reposo instantáneo y por tanto el eje instantáneo de rotación pasa por ellos). Este eje es paralelo al eje Z
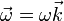
Esta velocidad se relaciona con la del CM observando que la velocidad del punto A debe ser nula
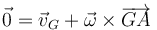
donde
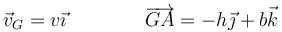
esto nos da
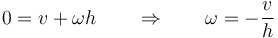
Esto da el momento cinético
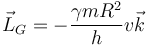
cuya derivada temporal vale
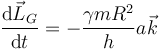
Esta cantidad debe ser igual a la resultante de los momentos de las fuerzas aplicadas
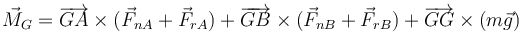
De estos términos, las fuerzas normales tienen momento nulo, por ser radiales y el peso también, por actuar sobre el propio CM. Queda
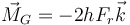
y por tanto
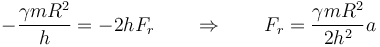
Llevamos esto a la ecuación para la aceleración
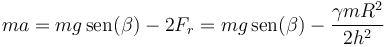
y de aquí despejamos la aceleración
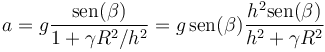
Conocida la aceleración tenemos el valor de la fuerza de rozamiento estático
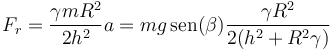
El límite de la inclinación lo da el que esta fuerza sea menor que la normal multiplicada por el coeficiente de rozamiento
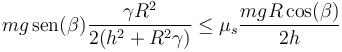
que, en términos del ángulo, queda
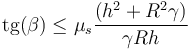
3 Con rozamiento por rodadura
Si se añade una fuerza de rozamiento proporcional a la fuerza normal, el único cambio es que
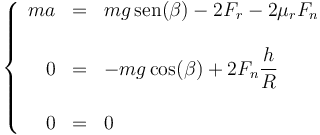
puesto que el valor de la fuerza normal no ha cambiado
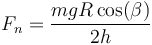
el único cambio en el resultado es

Esto nos proporciona una forma de medir el efecto del rozamiento por rodadura. Si conocemos la aceleración para diferentes ángulos, podemos establecer la relación
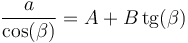
con
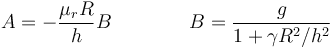
con lo cual, ajustando una recta por el método de mínimos cuadrados resulta