Caso práctico de ciclo Diesel (GIE)
De Laplace
| Línea 7: | Línea 7: | ||
El volumen inicial y tras la compresión los obtenemos de que conocemos la cilindrada y la relación de compresión | El volumen inicial y tras la compresión los obtenemos de que conocemos la cilindrada y la relación de compresión | ||
| - | <center><math>V_A-V_B=1700\,\mathrm{cm}^3\qquad\qquad \frac{V_A}{V_B}=18</math></center> | + | <center><math>V_A-V_B=1700\,\mathrm{cm}^3\qquad\qquad \frac{V_A}{V_B}=r=18</math></center> |
lo que nos da | lo que nos da | ||
| Línea 22: | Línea 22: | ||
|- | |- | ||
! Estado | ! Estado | ||
| - | ! p ( | + | ! p (MPa) |
! T (K) | ! T (K) | ||
! V (cm³) | ! V (cm³) | ||
|- | |- | ||
! A | ! A | ||
| - | | 150 | + | | 0.150 |
| 290 | | 290 | ||
| 1800 | | 1800 | ||
| Línea 34: | Línea 34: | ||
===Estado B (tras la compresión)=== | ===Estado B (tras la compresión)=== | ||
Si, como aproximación, suponemos que el proceso es adiabático y cuasiestático, podemos emplear la fórmula de Poisson | Si, como aproximación, suponemos que el proceso es adiabático y cuasiestático, podemos emplear la fórmula de Poisson | ||
| + | |||
| + | <center><math>p_AV_A^\gamma = p_B V_B^\gamma\qquad\Rightarrow\qquad p_B = p_A r^\gamma</math></center> | ||
| + | |||
| + | lo que da | ||
| + | |||
| + | <center><math>p_B = 150\times 18^{1.4}\,\mathrm{kPa}=8580\,\mathrm{kPa}=8.58\,\mathrm{MPa}</math></center> | ||
| + | |||
| + | La temperatura la podemos calcular empleando la ley de Poisson | ||
| + | |||
| + | <center><math>T_AV_A^{\gamma-1}=T_BV_B^{\gamma-1}\qquad\Rightarrow T_B = T_A r^{\gamma-1}</math></center> | ||
| + | |||
| + | o la de los gases ideales | ||
| + | |||
| + | <center><math>\frac{p_AV_A}{T_A}=\frac{p_BV_B}{T_B}\qquad\Rightarrow\qquad T_B=T_A\,\frac{p_B}{p_A}\,\frac{V_B}{V_A}</math></center> | ||
| + | |||
| + | y resulta | ||
| + | |||
| + | <center><math>T_B = 922\,\mathrm{K}</math></center> | ||
| + | |||
| + | Añadimos la fila a la tabla | ||
| + | |||
| + | {| class="bordeado" | ||
| + | |- | ||
| + | ! Estado | ||
| + | ! p (MPa) | ||
| + | ! T (K) | ||
| + | ! V (cm³) | ||
| + | |- | ||
| + | ! A | ||
| + | | 0.15 | ||
| + | | 290 | ||
| + | | 1800 | ||
| + | |- | ||
| + | ! A | ||
| + | | 8.58 | ||
| + | | 922 | ||
| + | | 100 | ||
| + | |} | ||
| + | |||
| + | === | ||
==Calor y trabajo== | ==Calor y trabajo== | ||
==Rendimiento== | ==Rendimiento== | ||
[[Categoría:Problemas de máquinas térmicas (GIE)]] | [[Categoría:Problemas de máquinas térmicas (GIE)]] | ||
Revisión de 10:58 28 may 2016
Contenido |
1 Enunciado
Suponga un motor diésel turbo con una cilindrada de 1700 cm³. En este motor el aire a la entrada está a una presión de 150 kPa y una temperatura de 17 °C. Si para este motor la razón de compresión es 18 y la de combustión vale 2, determine los volúmenes, presiones y temperaturas de cada vértice del ciclo, así como su rendimiento y el calor y el trabajo intercambiados por el motor.
2 Presiones, volúmenes y temperaturas
2.1 Estado A (antes de la compresión)
El volumen inicial y tras la compresión los obtenemos de que conocemos la cilindrada y la relación de compresión
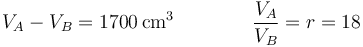
lo que nos da

La presión y la temperatura antes de la compresión son datos del problema

Construimos una tabla con estos valores, que iremos ampliando más tarde
| Estado | p (MPa) | T (K) | V (cm³) |
|---|---|---|---|
| A | 0.150 | 290 | 1800 |
2.2 Estado B (tras la compresión)
Si, como aproximación, suponemos que el proceso es adiabático y cuasiestático, podemos emplear la fórmula de Poisson
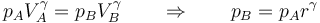
lo que da
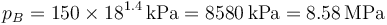
La temperatura la podemos calcular empleando la ley de Poisson

o la de los gases ideales
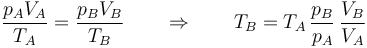
y resulta
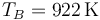
Añadimos la fila a la tabla
| Estado | p (MPa) | T (K) | V (cm³) |
|---|---|---|---|
| A | 0.15 | 290 | 1800 |
| A | 8.58 | 922 | 100 |





