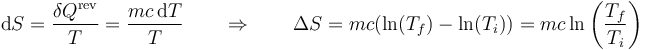Trabajo máximo en sistema de dos líquidos
De Laplace
(Página creada con '==Enunciado== Se tienen dos recipientes adiabáticos conteniendo 1.0 kg de agua cada uno, a 27°C y 90°C respectivamente. Se ponen en contacto a través de una par…') |
|||
| Línea 10: | Línea 10: | ||
<li>Determine el trabajo que se puede extraer del sistema.</li> | <li>Determine el trabajo que se puede extraer del sistema.</li> | ||
</ol> | </ol> | ||
| + | ==Contacto directo== | ||
| + | La primera parte del problema es idéntica a la de otro problema de [[Mezcla_de_dos_cantidades_de_agua|mezcla de dos cantidades de agua]]. | ||
| + | |||
| + | ===Temperatura final=== | ||
| + | Al ser un recipiente adiabático, no entra calor del exterior, por lo que todo lo que sale del recipiente 2 (el de 90%deg;C) entra en el 1 (el de 27°C) | ||
| + | |||
| + | <center><math>Q_\mathrm{2,out}=Q_\mathrm{1,in}\,</math></center> | ||
| + | |||
| + | La transferencia de calor se detiene cuando las temperaturas se igualan, por lo que queda | ||
| + | |||
| + | <center><math>m_2 c_2(T_2-T_f)=m_1c_1(T_f - T_1)\,</math></center> | ||
| + | |||
| + | y despejando | ||
| + | |||
| + | <center><math>T_f=\frac{m_1c_1 T_1+m_2c_2 T_2}{m_1c_1+m_2c_2}</math></center> | ||
| + | |||
| + | En este caso tanto las masas como los calores específicos son iguales, por lo que resulta una temperatura final que es la media aritmética de las dos iniciales | ||
| + | |||
| + | <center><math>T_f = \frac{T_1+T_2}{2}=58.5\,^\circ\mathrm{C}</math></center> | ||
| + | |||
| + | ===Calor transferido=== | ||
| + | Una vez que tenemos la temperatura final, hallamos la cantidad de calor que pasa de una cámara a la otra. | ||
| + | |||
| + | <center><math>Q_\mathrm{2,out}=1.0\mathrm{kg}\times 4.18\frac{\mathrm{kJ}}{\mathrm{kg}\cdot\mathrm{K}}(90-58.5)\mathrm{K}=131.7\mathrm{kJ}</math></center> | ||
| + | |||
| + | ===Producción de entropía=== | ||
| + | Para hallar la variación de entropía no basta con dividir el calor por la temperatura, sino que hay que suponer un proceso cuasiestático. En ese caso, resulta, para cada sistema | ||
| + | |||
| + | <center><math>\mathrm{d}S=\frac{\delta Q^\mathrm{rev}}{T}=\frac{mc\,\mathrm{d}T}{T}\qquad\Rightarrow\qquad \Delta S = mc(\ln(T_f)-\ln(T_i))=mc\ln\left(\frac{T_f}{T_i}\right)</math></center> | ||
| + | ==Contacto a través de una pared== | ||
[[Categoría:Problemas del segundo principio de la termodinámica (GIE)]] | [[Categoría:Problemas del segundo principio de la termodinámica (GIE)]] | ||
Revisión de 19:52 24 may 2016
Contenido |
1 Enunciado
Se tienen dos recipientes adiabáticos conteniendo 1.0 kg de agua cada uno, a 27°C y 90°C respectivamente. Se ponen en contacto a través de una pared diaterma. Halle:
- La temperatura final del agua.
- La cantidad de calor transferida.
- La variación de entropía en el proceso.
Suponga ahora que el contacto térmico no se hace directamente sino a través de una máquina térmica reversible que usa los recipientes como foco caliente y foco frío. Teniendo en cuenta que todos los procesos son reversibles
- Halle la temperatura final del agua
- Calcule el calor cedido por el agua caliente y el absorbido por el agua fría
- Determine el trabajo que se puede extraer del sistema.
2 Contacto directo
La primera parte del problema es idéntica a la de otro problema de mezcla de dos cantidades de agua.
2.1 Temperatura final
Al ser un recipiente adiabático, no entra calor del exterior, por lo que todo lo que sale del recipiente 2 (el de 90%deg;C) entra en el 1 (el de 27°C)
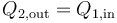
La transferencia de calor se detiene cuando las temperaturas se igualan, por lo que queda
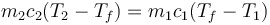
y despejando
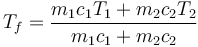
En este caso tanto las masas como los calores específicos son iguales, por lo que resulta una temperatura final que es la media aritmética de las dos iniciales

2.2 Calor transferido
Una vez que tenemos la temperatura final, hallamos la cantidad de calor que pasa de una cámara a la otra.
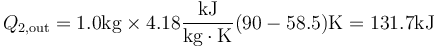
2.3 Producción de entropía
Para hallar la variación de entropía no basta con dividir el calor por la temperatura, sino que hay que suponer un proceso cuasiestático. En ese caso, resulta, para cada sistema