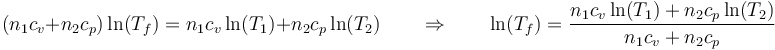Trabajo máximo en sistema de dos gases
De Laplace
| Línea 5: | Línea 5: | ||
<center>[[Archivo:maquina-dos-tanques.png|200px]]</center> | <center>[[Archivo:maquina-dos-tanques.png|200px]]</center> | ||
==Temperatura final== | ==Temperatura final== | ||
| + | El trabajo máximo se consigue cuando todos los procesos mecánicos o térmicos son reversibles, esto es, cuando no se produce entropía. | ||
| + | |||
| + | La máquina térmica situada entre los dos gases funcionará hasta que se iguale la temperatura de los dos gases sin producción de entropía. | ||
| + | |||
| + | La variación de entropía del foco caliente, teniendo en cuenta que está a volumen constante, será | ||
| + | |||
| + | <center><math>\Delta S_1 =n_1 c_v\ln\left(\frac{T_f}{T_1}\right)</math></center> | ||
| + | |||
| + | y la del foco frío, que se halla a presión constante | ||
| + | |||
| + | <center><math>\Delta S_2 =n_2 c_p\ln\left(\frac{T_f}{T_2}\right)</math></center> | ||
| + | |||
| + | Puesto que la entropía total no cambia en el proceso óptimo | ||
| + | |||
| + | <center><math>0 = \Delta S_1+\Delta S_2 = n_1 c_v\ln\left(\frac{T_f}{T_1}\right)+n_2 c_p\ln\left(\frac{T_f}{T_2}\right)</math></center> | ||
| + | |||
| + | Aplicamos las propiedades de los logaritmos y queda | ||
| + | |||
| + | <center><math>(n_1c_v+n_2c_p)\ln(T_f)=n_1c_v\ln(T_1)+n_2c_p\ln(T_2)\qquad\Rightarrow\qquad \ln(T_f)=\frac{n_1c_v\ln(T_1)+n_2c_p\ln(T_2)}{n_1c_v+n_2c_p}</math></center> | ||
==Trabajo máximo== | ==Trabajo máximo== | ||
[[Categoría:Problemas del segundo principio de la termodinámica (GIE)]] | [[Categoría:Problemas del segundo principio de la termodinámica (GIE)]] | ||
Revisión de 16:54 23 may 2016
Contenido |
1 Enunciado
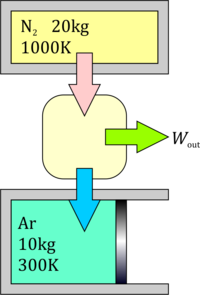
Un tanque de volumen constante contiene 20 kg de nitrógeno a 1000 K y un cilindro a presión constante contiene 10 kg de argón a 300K. Una máquina térmica situada entre el tanque y el cilindro, la cual extrae calor del tanque, realiza un cierto trabajo y expulsa calor al cilindro. Calcule el máximo trabajo que se puede realizar y las temperaturas finales del nitrógeno y el argón en ese caso.
2 Temperatura final
El trabajo máximo se consigue cuando todos los procesos mecánicos o térmicos son reversibles, esto es, cuando no se produce entropía.
La máquina térmica situada entre los dos gases funcionará hasta que se iguale la temperatura de los dos gases sin producción de entropía.
La variación de entropía del foco caliente, teniendo en cuenta que está a volumen constante, será
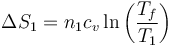
y la del foco frío, que se halla a presión constante
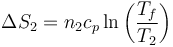
Puesto que la entropía total no cambia en el proceso óptimo
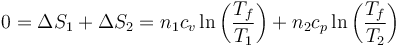
Aplicamos las propiedades de los logaritmos y queda