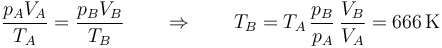Caso práctico de ciclo Otto
De Laplace
| Línea 27: | Línea 27: | ||
Con esto ya tenemos el punto de partida | Con esto ya tenemos el punto de partida | ||
| + | |||
| + | |||
| + | {| class="bordeado" | ||
| + | |- | ||
| + | ! Estado | ||
| + | ! p (kPa) | ||
| + | ! T (K) | ||
| + | ! V (cm³) | ||
| + | |- | ||
| + | ! A | ||
| + | | 100 | ||
| + | | 290 | ||
| + | | 1600 | ||
| + | |} | ||
| + | |||
| + | Para ir del estado A al B se realiza una compresión adiabática. Como suponemos que es cuasiestática, podemos aplicar la ley de Poisson | ||
| + | |||
| + | <center><math>p_AV_A^\gamma = p_B V_B^\gamma\,</math></center> | ||
| + | |||
| + | lo que nos permite hallar la presión en B | ||
| + | |||
| + | <center><math>p_B = p_A\left(\frac{V_A}{V_B}\right)^\gamma = p_A r^\gamma</math></center> | ||
| + | |||
| + | lo que da | ||
| + | |||
| + | <center><math>p_B = 100\times 8^1.4\,\mathrm{kPa} = 1840\,\mathrm{kPa}</math></center> | ||
| + | |||
| + | Conocidas la presión y el volumen, tenemos la temperatura por la ley de los gases ideales | ||
| + | |||
| + | <center><math>\frac{p_AV_A}{T_A}=\frac{p_BV_B}{T_B}\qquad \Rightarrow\qquad T_B = T_A\,\frac{p_B}{p_A}\,\frac{V_B}{V_A}= 666\,\mathrm{K}</math></center> | ||
| + | |||
Revisión de 22:57 19 abr 2016
Contenido |
1 Enunciado
Suponga un motor de gasolina de 1400 cm³ de cilindrada que se puede modelar mediante un ciclo Otto ideal con una relación de compresión de 8. Al inicio de la fase de compresión, el aire está a 100 kPa y 17°C. En la combustión se añaden 800 kJ/kg de calor. Determine la temperatura y la presión máximas que se producen en el ciclo, la salida de trabajo neto y el rendimiento de este motor.
Si este motor trabaja a 3000rpm, ¿cuánto es la potencia generada?
2 Estados del ciclo
El ciclo Otto ideal sirve para modelar el comportamiento de un motor de gasolina y está formado por dos isócoras y dos adiabáticas.
Estos cuatro procesos se pueden representar por segmentos rectos o curvos en un diagrama pV. Los vértices corresponden a 4 estados de equilibrio de forma que el proceso es A→B→C→D→A.
Denominaremos estado A al que tiene el gas antes de la compresión.
En este estado la temperatura es de 290 K y la presión es de 100 kPa.
El volumen inicial lo obtenemos de que conocemos la cilindrada
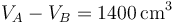
y la relación de compresión
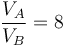
Despejando y sustituyendo obtenemos que

Con esto ya tenemos el punto de partida
| Estado | p (kPa) | T (K) | V (cm³) |
|---|---|---|---|
| A | 100 | 290 | 1600 |
Para ir del estado A al B se realiza una compresión adiabática. Como suponemos que es cuasiestática, podemos aplicar la ley de Poisson
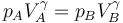
lo que nos permite hallar la presión en B
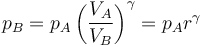
lo que da
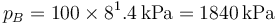
Conocidas la presión y el volumen, tenemos la temperatura por la ley de los gases ideales