Diferenciales
De Laplace
(→Introducción) |
(→Introducción) |
||
| Línea 10: | Línea 10: | ||
Eso sí, para poder sumar, primero debemos poder expresar correctamente los diferenciales de línea, de superficie o de volumen. Y su expresión dependerá del sistema de coordenadas que estemos empleando. Vamos a ello. | Eso sí, para poder sumar, primero debemos poder expresar correctamente los diferenciales de línea, de superficie o de volumen. Y su expresión dependerá del sistema de coordenadas que estemos empleando. Vamos a ello. | ||
| + | |||
| + | ==Diferenciales de camino== | ||
| + | |||
| + | ==Diferenciales de superficie== | ||
| + | |||
| + | ==Diferenciales de volumen== | ||
| + | |||
| + | ==Enlaces== | ||
| + | * '''Siguiente:''' | ||
| + | * '''Anterior:''' | ||
| + | |||
| + | [[Categoría:Diferenciales]] | ||
Revisión de 15:35 22 nov 2007
Contenido |
1 Introducción
Una de las operaciones que más a menudo se efectúan sobre los campos es la integración: sobre una línea, una superficie o un volumen y tanto integrales escalares como vectoriales.
Lo que nunca hay que perder de vista es que una integral es una suma de cosas muy pequeñitas. No tiene más misterio. Por ejemplo, si nos encontramos la integral
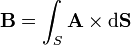
esto quiere decir simplemente que, dada una superficie  , la descomponemos en elementos diferenciales
, la descomponemos en elementos diferenciales  . Cada uno de esos vectores elementales se multiplica vectorialmente por el vector
. Cada uno de esos vectores elementales se multiplica vectorialmente por el vector
 y se suman todos esos productos. Como la suma de vectores es un vector, el resultado de la integral será una cantidad vectorial. Y eso es todo. No hay que quebrarse la cabeza meditando si es un flujo o una circulación, si hay que poner tal o cual jacobiano, o si podemos hallar una primitiva. Solo hay que sumar.
y se suman todos esos productos. Como la suma de vectores es un vector, el resultado de la integral será una cantidad vectorial. Y eso es todo. No hay que quebrarse la cabeza meditando si es un flujo o una circulación, si hay que poner tal o cual jacobiano, o si podemos hallar una primitiva. Solo hay que sumar.
Eso sí, para poder sumar, primero debemos poder expresar correctamente los diferenciales de línea, de superficie o de volumen. Y su expresión dependerá del sistema de coordenadas que estemos empleando. Vamos a ello.
2 Diferenciales de camino
3 Diferenciales de superficie
4 Diferenciales de volumen
5 Enlaces
- Siguiente:
- Anterior:





