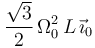No Boletín - Placa triangular (Ex.Ene/16)
De Laplace
(→Caracterización de los movimientos elementales {01} y {20}) |
(→Caracterización de los movimientos elementales {01} y {20}) |
||
| Línea 16: | Línea 16: | ||
\left\{\begin{array}{l} \vec{\omega}_{01}(t)=\omega_0\,\vec{k}_0 \\ \\ \vec{v}^{\, O}_{01}(t)=\vec{0} \end{array}\right.\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \left\{\begin{array}{l} \vec{\omega}_{20}(t)=\Omega_0\,\vec{\jmath}_0 \\ \\ \vec{v}^{\, D}_{20}(t)=\vec{0} \end{array}\right.\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \left|\begin{array}{l} \overrightarrow{OD}=\displaystyle\frac{\sqrt{3}}{2}\,L\,\vec{\imath}_0 \\ \\ \overrightarrow{DO}=-\overrightarrow{OD}=-\displaystyle\frac{\sqrt{3}}{2}\,L\,\vec{\imath}_0 \end{array}\right. | \left\{\begin{array}{l} \vec{\omega}_{01}(t)=\omega_0\,\vec{k}_0 \\ \\ \vec{v}^{\, O}_{01}(t)=\vec{0} \end{array}\right.\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \left\{\begin{array}{l} \vec{\omega}_{20}(t)=\Omega_0\,\vec{\jmath}_0 \\ \\ \vec{v}^{\, D}_{20}(t)=\vec{0} \end{array}\right.\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \left|\begin{array}{l} \overrightarrow{OD}=\displaystyle\frac{\sqrt{3}}{2}\,L\,\vec{\imath}_0 \\ \\ \overrightarrow{DO}=-\overrightarrow{OD}=-\displaystyle\frac{\sqrt{3}}{2}\,L\,\vec{\imath}_0 \end{array}\right. | ||
</math></center> | </math></center> | ||
| - | habiéndose tenido en cuenta que el punto <math>O\,</math> pertenece al eje permanente de rotación | + | habiéndose tenido en cuenta que el punto <math>O\,</math> es un punto fijo en el movimiento {01} porque pertenece al eje permanente de rotación de dicho movimiento (eje <math>O_1Z_1\,</math>), y que el punto <math>D\,</math> es un punto fijo en el movimiento {20} porque pertenece al eje permanente de rotación de dicho movimiento (recta que pasa por los puntos <math>\,A\,</math> y <math>\,B\,</math>). |
Con vistas al cálculo de aceleraciones, resulta interesante determinar también en los movimientos {01} y {20} las aceleraciones angulares y las aceleraciones de aquellos puntos cuyas velocidades son conocidas en todo instante: | Con vistas al cálculo de aceleraciones, resulta interesante determinar también en los movimientos {01} y {20} las aceleraciones angulares y las aceleraciones de aquellos puntos cuyas velocidades son conocidas en todo instante: | ||
Revisión de 17:51 14 mar 2016
Contenido |
1 Enunciado
Una placa triangular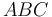 
(sólido "2"), equilátera de lado 
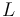, rota con velocidad angular constante 
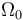(en el sentido indicado en la figura) alrededor del lado 
de un armazón triangular hueco 
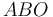(sólido "0") que tiene exactamente las mismas dimensiones que la placa. A su vez, el armazón 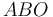se mantiene en todo instante en un plano horizontal paralelo al plano 
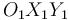del triedro fijo 
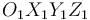(sólido "1"), y rota con velocidad angular constante 
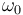(en el sentido indicado en la figura) alrededor del eje vertical fijo que pasa por su vértice 
(eje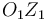 
). Sea 
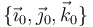la base ortonormal asociada al triedro 
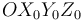(sólido "0") definido en la figura, el cual se mueve solidariamente con el armazón triangular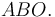 
Determine las siguientes magnitudes:
- Velocidad
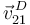(ver 
en la figura)
- Aceleración angular
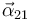
- Aceleración
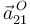
2 Caracterización de los movimientos elementales {01} y {20}
Los datos contenidos en el enunciado nos permiten expresar en la base vectorial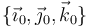 
, asociada al triedro 
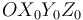, las reducciones cinemáticas del movimiento {01} (en el punto 
) y del movimiento {20} (en el punto 
), así como un par de vectores geométricos que necesitaremos más adelante:
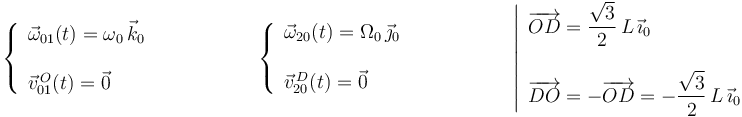
habiéndose tenido en cuenta que el punto es un punto fijo en el movimiento {01} porque pertenece al eje permanente de rotación de dicho movimiento (eje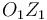 
), y que el punto es un punto fijo en el movimiento {20} porque pertenece al eje permanente de rotación de dicho movimiento (recta que pasa por los puntos 
y 
).
Con vistas al cálculo de aceleraciones, resulta interesante determinar también en los movimientos {01} y {20} las aceleraciones angulares y las aceleraciones de aquellos puntos cuyas velocidades son conocidas en todo instante:
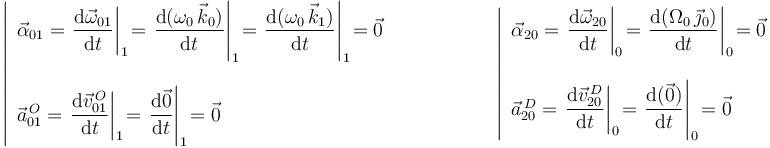
3 Velocidad {21} del punto D
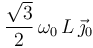
4 Aceleración angular {21}
5 Aceleración {21} del punto O
