última version al 16:30 12 feb 2016

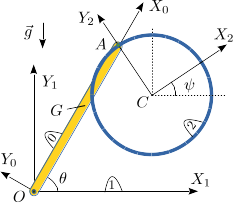
1 Aro colgando de una barra que rota

La barra homogénea $O A$ (sólido "0") tiene masa $m$ y longitud $L$ . Está articulada en el punto fijo $O$ y rota de modo que está siempre contenida en el plano $O X 1 Y 1$ . En su extremo $A$ está articulado un aro homogéneo de radio $R$ y masa $m$ (sólido "2"). El sistema está sometido a la acción de la gravedad. Se recomienda utilizar los ángulos ${θ,ψ}$ como coordenadas para resolver el problema.

Determina las reducciones cinemáticas de los movimientos {01}, {21}, {20}.
Calcula las energías cinética y potencial totales del sistema.
Usando las herramientas de la Dinámica Analítica, encuentra las ecuaciones de movimiento.
Se impone el vínculo cinemático 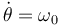$\dot{\theta}=\omega_0$ . Determina el par necesario para imponer dicho vínculo. Supón que en el instante inicial se tiene $θ(0) = 0$ , $ψ(0) = 0$ .
Supongamos que las coordenadas ${θ,ψ}$ son de nuevo libres. Supón que se tiene $θ(0) = 0$ , $ψ(0) = 0$ . En ese instante una percusión $\vec{\hat{F}}=[\hat{F}_0,\hat{F}_0,0]_1$ actúa sobre el punto $A$ . Determina el estado cinemático del sistema justo después de la percusión.

2 Barra articulada sobre muelle

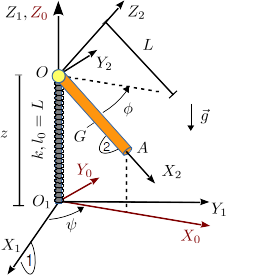
En el sistema de la figura, la barra delgada homogénea $O A$ (sólido "2"), de masa $m$ y longitud $L$ , está articulada en el punto $O$ . El punto $O$ puede moverse sobre el eje fijo $O 1 Z 1$ , y está conectado a un muelle de constante elástica $k$ y longitud natural $L$ . El muelle siempre permanece vertical. La barra "2" está siempre contenida en el plano $O 1 X 0 Z 0$ , como se indica en la figura.

Encuentra la reducción cinemática del movimiento {21} en los puntos $O$ y $G$ .
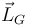Calcula el momento cinético de la barra "2" en $O$ y $G$ ( $\vec{L}_O$ , $\vec{L}_G$ ).
Calcula la energía cinética de la barra "2".
Aplicando el T.C.M. y el T.M.C. escribe las ecuaciones de movimiento del sistema.
Escribe todas las integrales primeras del movimiento que puedas encontrar.

@@ Línea 9: / Línea 9: @@
 #Se impone el vínculo cinemático <math>\dot{\theta}=\omega_0</math>. Determina el par necesario para imponer dicho vínculo. Supón que en el instante inicial se tiene <math>\theta(0)=0</math>, <math>\psi(0)=0</math>.
 #Supongamos que las coordenadas <math>\{\theta, \psi\}</math> son de nuevo libres. Supón que se tiene <math>\theta(0)=0</math>, <math>\psi(0)=0</math>. En ese instante una percusión <math>\vec{\hat{F}}=[\hat{F}_0,\hat{F}_0,0]_1</math> actúa sobre el punto <math>A</math>. Determina el estado cinemático del sistema justo después de la percusión.
+=[[Barra articulada sobre muelle Enero 2015 (MR G.I.C.)|Barra articulada sobre muelle]] =
+[[Imagen:MR_barra_articulada_muelle_enunciado.png|right]]
+En el sistema de la figura, la barra delgada homogénea <math>OA</math> (sólido "2"), de masa <math>m</math> y longitud <math>L</math>, está articulada en el punto <math>O</math>. El punto <math>O</math> puede moverse sobre el eje fijo <math>O_1Z_1</math>, y está conectado a un muelle de constante elástica <math>k</math> y longitud natural <math>L</math>. El muelle siempre permanece vertical.  La barra "2"  está siempre contenida en el plano <math>O_1X_0Z_0</math>, como se indica en la figura.
+#Encuentra la reducción cinemática del movimiento {21} en los puntos <math>O</math> y <math>G</math>.
+#Calcula el momento cinético de la barra "2" en <math>O</math> y <math>G</math> (<math>\vec{L}_O</math>, <math>\vec{L}_G</math>).
+#Calcula la energía cinética de la barra "2".
+#Aplicando el T.C.M. y el T.M.C. escribe las ecuaciones de movimiento del sistema.
+#Escribe todas las integrales primeras del movimiento que puedas encontrar.

Primera Convocatoria Ordinaria 2015/16 (MR G.I.C.)

De Laplace

última version al 16:30 12 feb 2016

1 Aro colgando de una barra que rota

2 Barra articulada sobre muelle

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES