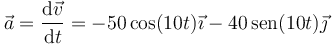Partícula en movimiento elíptico
De Laplace
(Diferencias entre revisiones)
| Línea 8: | Línea 8: | ||
# Demuestre que la partícula obedece la ley de Hooke (con longitud natural nula). ¿Cuánto vale la constante del resorte? ¿Cuánto vale la energía mecánica de la partícula en cada instante? ¿Es constante esta magnitud? | # Demuestre que la partícula obedece la ley de Hooke (con longitud natural nula). ¿Cuánto vale la constante del resorte? ¿Cuánto vale la energía mecánica de la partícula en cada instante? ¿Es constante esta magnitud? | ||
| + | ==Velocidad y aceleración== | ||
| + | Hallamos la velocidad derivando respecto al tiempo el vector de posición | ||
| + | |||
| + | <center><math>\vec{v}=\frac{\mathrm{d}\vec{r}}{\mathrm{d}t}=-5.0\,\mathrm{sen}(10t)\vec{\imath}+4.0\cos(10t)\vec{\jmath}</math></center> | ||
| + | |||
| + | y la aceleración como la derivada temporal de la velocidad | ||
| + | |||
| + | <center><math>\vec{a}=\frac{\mathrm{d}\vec{v}}{\mathrm{d}t}=-50\cos(10t)\vec{\imath}-40\,\mathrm{sen}(10t)\vec{\jmath}</math></center> | ||
| + | |||
| + | ==Centros de curvatura== | ||
| + | ==Cálculo de magnitudes== | ||
| + | ==Ley de Hooke== | ||
[[Categoría:Problemas de cinemática de la partícula (GIE)]] | [[Categoría:Problemas de cinemática de la partícula (GIE)]] | ||
[[Categoría:Problemas de energía y leyes de conservación (GIE)]] | [[Categoría:Problemas de energía y leyes de conservación (GIE)]] | ||
Revisión de 20:00 2 sep 2015
Una partícula de masa 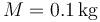 describe el movimiento elíptico (en el SI)
describe el movimiento elíptico (en el SI)
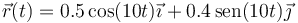
- Calcule la velocidad y la aceleración de la partícula en todo instante.
- Determine la posición del centro de curvatura de la partícula en
 y
y 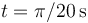 .
.
- Halle la cantidad de movimiento, el momento cinético de la partícula respecto al origen de coordenadas y la energía cinética para todo instante. ¿Es constante alguna de estas magnitudes?
- Demuestre que la partícula obedece la ley de Hooke (con longitud natural nula). ¿Cuánto vale la constante del resorte? ¿Cuánto vale la energía mecánica de la partícula en cada instante? ¿Es constante esta magnitud?
Contenido |
1 Velocidad y aceleración
Hallamos la velocidad derivando respecto al tiempo el vector de posición

y la aceleración como la derivada temporal de la velocidad