Partícula en movimiento elíptico
De Laplace
Contenido |
1 Enunciado
Una partícula de masa 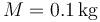 describe el movimiento elíptico (en el SI)
describe el movimiento elíptico (en el SI)
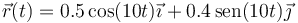
- Calcule la velocidad y la aceleración de la partícula en todo instante.
- Determine la posición del centro de curvatura de la partícula en
 y
y 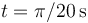 .
.
- Halle la cantidad de movimiento, el momento cinético de la partícula respecto al origen de coordenadas y la energía cinética para todo instante. ¿Es constante alguna de estas magnitudes?
- Demuestre que la partícula obedece la ley de Hooke (con longitud natural nula). ¿Cuánto vale la constante del resorte? ¿Cuánto vale la energía mecánica de la partícula en cada instante? ¿Es constante esta magnitud?
2 Velocidad y aceleración
En lo que sigue todas las magnitudes se consideran en las unidades fundamentales del SI.
Hallamos la velocidad derivando respecto al tiempo el vector de posición

y la aceleración como la derivada temporal de la velocidad
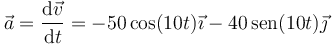
3 Centros de curvatura
El centro de curvatura se calcula como
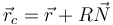
siendo R el radio de curvatura y  el vector normal a la trayectoria.
el vector normal a la trayectoria.
3.1 En t = 0
En el instante inicial, las magnitudes cinemáticas valen

Esta aceleración es puramente normal a la velocidad, por lo que el vector normal es
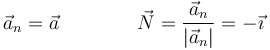
y el radio de curvatura vale
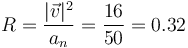
lo que nos da el centro de curvatura

3.2 En t = π/20
Cuando t = π / 20, 10t = π / 2 y las expresiones se simplifican a

De nuevo la aceleración es puramente normal a la velocidad, por lo que el vector normal es

y el radio de curvatura vale ahora
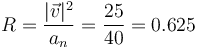
lo que nos da el centro de curvatura
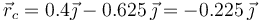
4 Cálculo de magnitudes
4.1 Cantidad de movimiento
Es el producto de la masa por la velocidad

que obviamente no es una constante de movimiento.
4.2 Momento cinético
Es el producto vectorial de la posición por la cantidad de movimiento
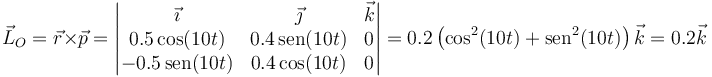
que sí es una constante de movimiento. Esto se debe a que la fuerza que actúa sobre la partícula es una fuerza central.
4.3 Energía cinética
Por último, la energía cinética es igual a
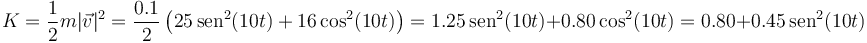
Esta cantidad tampoco es una constante de movimiento.
5 Ley de Hooke
La ley de Hooke, para longitud natural nula, es de la forma
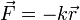
En nuestro caso, la fuerza que actúa sobre la partícula, es

Esta fuerza es efectivamente proporcional al vector de posición
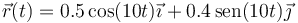
siendo la constante elástica, como se comprueba fácilmente,
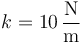
Esta cantidad cumple k = mω2, como cabe esperar de un oscilador armónico, pero no es preciso emplear este dato.
La energía potencial asociada a esta fuerza tiene la expresión
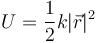
que, como función del tiempo queda
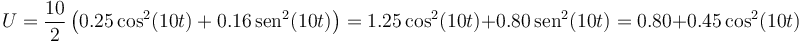
Esta cantidad tampoco es una constante.
No obstante, la energía mecánica, suma de la cinética y la potencial
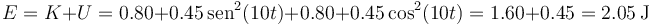
sí es una constante, como corresponde a que la fuerza elástica sea una fuerza conservativa.





