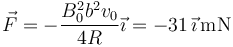Espira triangular que penetra en campo magnético
De Laplace
(→Valores numéricos) |
|||
| (5 ediciones intermedias no se muestran.) | |||
| Línea 33: | Línea 33: | ||
y resulta la corriente | y resulta la corriente | ||
| - | <center><math>I=-\frac{1}{R}\frac{\mathrm{d}\ }{\mathrm{d}t}\left(\frac{B_0bv_0^2 t^2}{2h}\right)=-\frac{B_0bv_0^2t}{ | + | <center><math>I=-\frac{1}{R}\frac{\mathrm{d}\ }{\mathrm{d}t}\left(\frac{B_0bv_0^2 t^2}{2h}\right)=-\frac{B_0bv_0^2t}{Rh}</math></center> |
El signo negativo indica que la corriente realmente va en sentido horario. | El signo negativo indica que la corriente realmente va en sentido horario. | ||
| Línea 39: | Línea 39: | ||
Este resultado vale solo para el intervalo de tiempo en que la espira entra en el campo. Antes de que entrara y una vez que ha penetrado por completo (lo cual ocurre a partir de <math>T=h/v_0</math>) el flujo magnético no cambia y la corriente es nula. Por tanto | Este resultado vale solo para el intervalo de tiempo en que la espira entra en el campo. Antes de que entrara y una vez que ha penetrado por completo (lo cual ocurre a partir de <math>T=h/v_0</math>) el flujo magnético no cambia y la corriente es nula. Por tanto | ||
| - | <center><math>I(t)=\begin{cases} 0 & t < 0 \\ & \\ -\dfrac{B_0bv_0^2t}{ | + | <center><math>I(t)=\begin{cases} 0 & t < 0 \\ & \\ -\dfrac{B_0bv_0^2t}{Rh} & 0 < t < \dfrac{h}{v_0} \\ & \\ 0 & t> \dfrac{h}{v_0}\end{cases}</math></center> |
==Energía disipada== | ==Energía disipada== | ||
| + | La energía se disipa por efecto Jooule sólo en el periodo en el que la espira está penetrando en el campo. Por tanto | ||
| + | |||
| + | <center><math>W_d = \int_0^{h/v_0} \frac{B_0^2b^2v_0^4 t^2}{Rh^2}\mathrm{d}t=\frac{B_0^2b^2v_0h}{3R}</math></center> | ||
| + | |||
==Fuerza en un instante== | ==Fuerza en un instante== | ||
| + | La fuerza sobre una espira inmersa parcialmente en un campo magnético uniforme es | ||
| + | |||
| + | <center><math>\vec{F}=I\int_P^Q \mathrm{d}\vec{r}\times\vec{B}=I\overrightarrow{PQ}\times\vec{B}</math></center> | ||
| + | |||
| + | siendo P el punto donde la espira penetra en el campo y Q por donde sale de él. En este caso | ||
| + | |||
| + | <center><math>\overrightarrow{PQ}=y(x=h/2)\vec{\jmath}=\frac{b}{2}\vec{\jmath}</math></center> | ||
| + | |||
| + | Esto nos da | ||
| + | |||
| + | <center><math>\vec{F}=I\left(\frac{b}{2}\vec{\jmath}\right)\times(B_0\vec{k})=\frac{IbB_0}{2}\vec{\imath}</math></center> | ||
| + | |||
| + | Sustituimos el valor de la intensidad de corriente en ese instante | ||
| + | |||
| + | <center><math>I\left(x=\frac{h}{2}\right) = I\left(t=\frac{h/v_0}{2}\right) = -\frac{B_0v_0 b}{2R}</math></center> | ||
| + | |||
| + | y queda | ||
| + | |||
| + | <center><math>\vec{F}=-\frac{B_0^2b^2 v_0}{4R}\vec{\imath}</math></center> | ||
| + | |||
| + | Obsérvese que no necesitamos descomponer el tramo en los dos segmentos rectilíneos. | ||
| + | |||
==Valores numéricos== | ==Valores numéricos== | ||
| + | La resistencia del hilo tiene el valor | ||
| + | |||
| + | <center><math>R = \frac{l}{\sigma A}</math></center> | ||
| + | |||
| + | donde la longitud es el perímetro del triángulo | ||
| + | |||
| + | <center><math>l = b+ \sqrt{b_1^2+h^2}+\sqrt{b_2^2+h^2}= 25\,\mathrm{cm}+15\,\mathrm{cm}+20\,\mathrm{cm}= 60\,\mathrm{cm}</math></center> | ||
| + | |||
| + | Nótese que éste es el único sitio donde se usan por separado <math>b_1</math> y <math>b_2</math>. Queda entonces | ||
| + | |||
| + | <center><math>R = \frac{0.60}{6\times 10^7\times 10^{-6}}\Omega = 0.010\,\Omega</math></center> | ||
| + | |||
| + | A partir de aquí tenemos: | ||
| + | |||
| + | ;Corriente como función del tiempo: para el intervalo en que la espira entra en el campo (<math>0 < t < 0.06\,\mathrm{s}</math>), y midiendo el tiempo en segundos y la corriente en amperios | ||
| + | |||
| + | <center><math>I(t) = -\frac{B_0bv_0^2t}{Rh}= -83.3t\,</math></center> | ||
| + | :Esta corriente varía de 0 a -5A. | ||
| + | ;Energía total disipada | ||
| + | |||
| + | <center><math>W_d = \frac{B_0^2b^2v_0h}{3Rh} = 5\,\mathrm{mJ}</math></center> | ||
| + | ;Fuerza sobre la espira | ||
| + | |||
| + | <center><math>\vec{F}=-\frac{B_0^2b^2 v_0}{4R}\vec{\imath}= -31\,\vec{\imath}\,\mathrm{mN}</math></center> | ||
[[Categoría:Problemas de inducción electromagnética (GIE)]] | [[Categoría:Problemas de inducción electromagnética (GIE)]] | ||
última version al 18:10 21 jun 2015
Contenido |
1 Enunciado
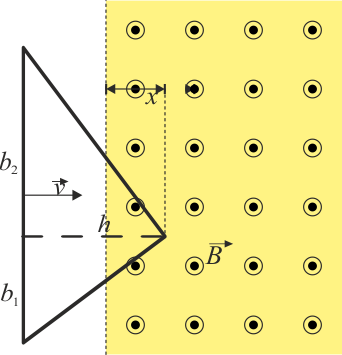
Una espira en forma de triángulo de altura h y base b = b1 + b2 penetra en un campo magnético uniforme 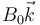 que se extiende en la región x > 0 tal como indica la figura (la base del triángulo es paralela al borde del campo). La espira es de un hilo de resistencia R.
que se extiende en la región x > 0 tal como indica la figura (la base del triángulo es paralela al borde del campo). La espira es de un hilo de resistencia R.
La espira se mueve con velocidad constante 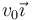 y penetra en el campo magnético en t = 0.
y penetra en el campo magnético en t = 0.
- Determine la corriente que circula por la espira como función del tiempo.
- Calcule la energía total disipada en ella desde que comienza a entrar hasta que penetra por completo.
- Halle la fuerza magnética sobre la espira para el instante en que ha penetrado hasta x = h / 2.
- Dé valores numéricos a los apartados anteriores si
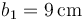 ,
, 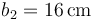 ,
, 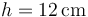 ,
, 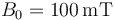 ,
, 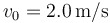 y el hilo tiene conductividad
y el hilo tiene conductividad 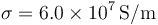 y sección
y sección 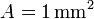 .
.
2 Corriente inducida
La corriente que circula por la espira se halla combinando la ley de Faraday y la de Ohm
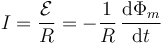
Considerando un sentido de recorrido antihorario de la espira, el flujo magnético es igual a
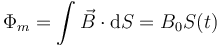
con S(t) el área del triángulo en el cual hay campo magnético. Este área vale

y por semejanza de triángulos
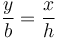
Dado que x = v0t queda finalmente
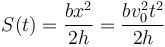
y resulta la corriente
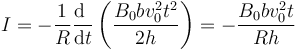
El signo negativo indica que la corriente realmente va en sentido horario.
Este resultado vale solo para el intervalo de tiempo en que la espira entra en el campo. Antes de que entrara y una vez que ha penetrado por completo (lo cual ocurre a partir de T = h / v0) el flujo magnético no cambia y la corriente es nula. Por tanto
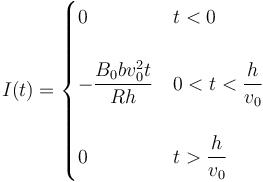
3 Energía disipada
La energía se disipa por efecto Jooule sólo en el periodo en el que la espira está penetrando en el campo. Por tanto
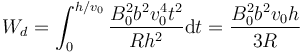
4 Fuerza en un instante
La fuerza sobre una espira inmersa parcialmente en un campo magnético uniforme es
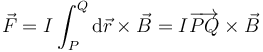
siendo P el punto donde la espira penetra en el campo y Q por donde sale de él. En este caso
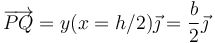
Esto nos da
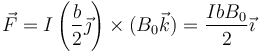
Sustituimos el valor de la intensidad de corriente en ese instante
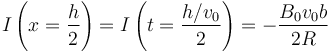
y queda
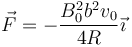
Obsérvese que no necesitamos descomponer el tramo en los dos segmentos rectilíneos.
5 Valores numéricos
La resistencia del hilo tiene el valor

donde la longitud es el perímetro del triángulo
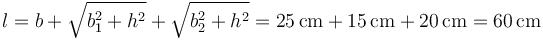
Nótese que éste es el único sitio donde se usan por separado b1 y b2. Queda entonces
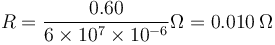
A partir de aquí tenemos:
- Corriente como función del tiempo
- para el intervalo en que la espira entra en el campo (
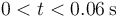 ), y midiendo el tiempo en segundos y la corriente en amperios
), y midiendo el tiempo en segundos y la corriente en amperios
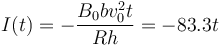
- Esta corriente varía de 0 a -5A.
- Energía total disipada

- Fuerza sobre la espira