Entrar Página Discusión Historial Go to the site toolbox

Rotación tridimensional de una partícula

De Laplace

(Diferencias entre revisiones)
(→A partir de su expresión vectorial)
 
(Una edición intermedia no se muestra.)
Línea 65: Línea 65:
<center><math>\vec{\alpha}=-0.50\frac{-12\vec{\imath}+20\vec{\jmath}+9\vec{k}}{25}=\left(0.24\vec{\imath}-0.40\vec{\jmath}-0.18\vec{k}\right)\frac{\mathrm{rad}}{\mathrm{s}^2}</math></center>
<center><math>\vec{\alpha}=-0.50\frac{-12\vec{\imath}+20\vec{\jmath}+9\vec{k}}{25}=\left(0.24\vec{\imath}-0.40\vec{\jmath}-0.18\vec{k}\right)\frac{\mathrm{rad}}{\mathrm{s}^2}</math></center>
-
Esto nos da la aceleración angular
+
Esto nos da la aceleración tangencial
<center><math>\vec{a}_t=\vec{\alpha}\times\vec{r}=\left(0.075\vec{\imath}+0.10\vec{k}\right)\frac{\mathrm{m}}{\mathrm{s}^2}</math></center>
<center><math>\vec{a}_t=\vec{\alpha}\times\vec{r}=\left(0.075\vec{\imath}+0.10\vec{k}\right)\frac{\mathrm{m}}{\mathrm{s}^2}</math></center>
Línea 72: Línea 72:
<center><math>a_t=\frac{\vec{a}_t\cdot\vec{v}}{|\vec{v}|}=-0.125\,\frac{\mathrm{m}}{\mathrm{s}^2}</math></center>
<center><math>a_t=\frac{\vec{a}_t\cdot\vec{v}}{|\vec{v}|}=-0.125\,\frac{\mathrm{m}}{\mathrm{s}^2}</math></center>
 +
====A partir de su módulo, dirección y sentido====
====A partir de su módulo, dirección y sentido====
Esta aceleración tangencial también puede calcularse observando que:
Esta aceleración tangencial también puede calcularse observando que:
Línea 97: Línea 98:
lo que en este caso da
lo que en este caso da
-
<center><math>\vec{}_n=\left|\begin{matrix}\vec{\imath} & \vec{\jmath} & \vec{k} \\ -12 & 20 & 9 \\ -3.75 & 0.00 & 5.00\end{matrix}\right| = \left(-100\vec{\imath}-93.75\vec{\jmath}-75\vec{k}\right)\frac{\mathrm{m}}{\mathrm{s}^2}</math></center>
+
<center><math>\vec{a}_n=\left|\begin{matrix}\vec{\imath} & \vec{\jmath} & \vec{k} \\ -12 & 20 & 9 \\ -3.75 & 0.00 & 5.00\end{matrix}\right| = \left(-100\vec{\imath}-93.75\vec{\jmath}-75\vec{k}\right)\frac{\mathrm{m}}{\mathrm{s}^2}</math></center>
y en forma escalar
y en forma escalar
<center><math>a_n=\left|\vec{a}_n\right| = 156.25\,\frac{\mathrm{m}}{\mathrm{s}^2}</math></center>
<center><math>a_n=\left|\vec{a}_n\right| = 156.25\,\frac{\mathrm{m}}{\mathrm{s}^2}</math></center>
 +
====A partir de su módulo, dirección y sentido====
====A partir de su módulo, dirección y sentido====
La aceleración normal en este movimiento puede también calcularse observando que:
La aceleración normal en este movimiento puede también calcularse observando que:

última version al 19:47 4 nov 2014

Contenido

1 Enunciado

Una partícula describe un movimiento circular alrededor del origen de forma que en un cierto instante su posición la da el vector

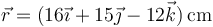
\vec{r}=(16\vec{\imath}+15\vec{\jmath} -12\vec{k})\,\mathrm{cm}

La velocidad angular de la partícula en el mismo instante es

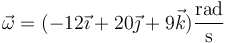
\vec{\omega}=(-12\vec{\imath}+20\vec{\jmath}+9\vec{k})\frac{\mathrm{rad}}{\mathrm{s}}

En el mismo instante la aceleración angular tiene sentido opuesto a la velocidad angular y módulo 0.50 rad/s². Para este instante, calcule:

  1. La velocidad lineal y la rapidez de la partícula.
  2. La aceleración tangencial y la aceleración normal, tanto escalares como vectores.
  3. Los vectores tangente y normal.
  4. El radio de curvatura y el centro de curvatura.

2 Velocidad y rapidez

En lo que sigue, en todos los cálculos se usará el SI, por lo que escribiremos la posición como

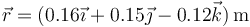
\vec{r}=(0.16\vec{\imath}+0.15\vec{\jmath} -0.12\vec{k})\,\mathrm{m}

2.1 Velocidad lineal

Para una partícula que describe un movimiento de rotación alrededor del origen, su velocidad instantánea la da

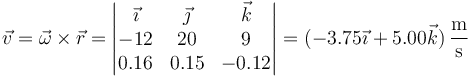
\vec{v}=\vec{\omega}\times\vec{r}=\left|\begin{matrix} \vec{\imath} & \vec{\jmath} & \vec{k} \\ -12 & 20 & 9 \\ 0.16 & 0.15 & -0.12\end{matrix}\right|=(-3.75\vec{\imath}+5.00\vec{k})\,\frac{\mathrm{m}}{\mathrm{s}}

2.2 Rapidez

La rapidez o celeridad es igual al módulo de la velocidad

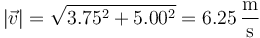
\left|\vec{v}\right| = \sqrt{3.75^2+5.00^2}=6.25\,\frac{\mathrm{m}}{\mathrm{s}}

Esta rapidez es igual a

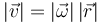
\left|\vec{v}\right| = \left|\vec{\omega}\right|\left|\vec{r}\right|

donde

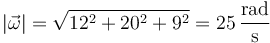
\left|\vec{\omega}\right|=\sqrt{12^2+20^2+9^2}=25\,\frac{\mathrm{rad}}{\mathrm{s}}

y

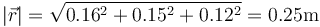
\left|\vec{r}\right|=\sqrt{0.16^2+0.15^2+0.12^2}=0.25\mathrm{m}

3 Componentes intrínsecas de la aceleración

La aceleración de una partícula en un movimiento circular alrededor del origen lo da la expresión vectorial

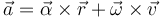
\vec{a}=\vec{\alpha}\times\vec{r}+\vec{\omega}\times\vec{v}

donde el primer término es la aceleración tangencial

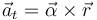
\vec{a}_t=\vec{\alpha}\times\vec{r}

y el segundo la normal

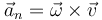
\vec{a}_n=\vec{\omega}\times\vec{v}

3.1 Aceleración tangencial

3.1.1 A partir de su expresión vectorial

Para calcular la aceleración tangencial necesitamos antes la aceleración angular. Por tratarse de un movimiento circular, la aceleración angular es paralela a la velocidad angular

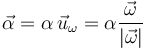
\vec{\alpha}=\alpha\,\vec{u}_\omega = \alpha\frac{\vec{\omega}}{|\vec{\omega}|}

Puesto que se nos dice que su módulo es 0.50rad/s² y su sentido opuesto al de la velocidad angular, el vector aceleración angular vale

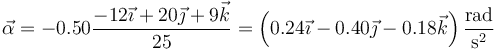
\vec{\alpha}=-0.50\frac{-12\vec{\imath}+20\vec{\jmath}+9\vec{k}}{25}=\left(0.24\vec{\imath}-0.40\vec{\jmath}-0.18\vec{k}\right)\frac{\mathrm{rad}}{\mathrm{s}^2}

Esto nos da la aceleración tangencial

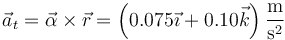
\vec{a}_t=\vec{\alpha}\times\vec{r}=\left(0.075\vec{\imath}+0.10\vec{k}\right)\frac{\mathrm{m}}{\mathrm{s}^2}

En forma escalar, proyectamos sobre la velocidad

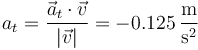
a_t=\frac{\vec{a}_t\cdot\vec{v}}{|\vec{v}|}=-0.125\,\frac{\mathrm{m}}{\mathrm{s}^2}

3.1.2 A partir de su módulo, dirección y sentido

Esta aceleración tangencial también puede calcularse observando que:

  • Es tangente a la velocidad, es decir, es paralela a
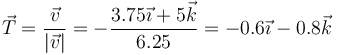
\vec{T}=\frac{\vec{v}}{|\vec{v}|}=-\frac{3.75\vec{\imath}+5\vec{k}}{6.25}=-0.6\vec{\imath}-0.8\vec{k}
  • Tiene módulo
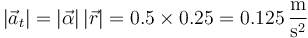
\left|\vec{a}_t\right|=\left|\vec{\alpha}\right|\left|\vec{r}\right|=0.5\times 0.25=0.125\,\frac{\mathrm{m}}{\mathrm{s}^2}
  • Puesto que la aceleración angular 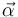\vec{\alpha} es opuesta a la velocidad angular, la aceleración tangencial es opuesta a la velocidad.

Por tanto

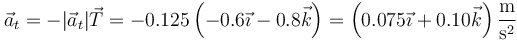
\vec{a}_t = -|\vec{a}_t|\vec{T}=-0.125\left(-0.6\vec{\imath}-0.8\vec{k}\right)=\left(0.075\vec{\imath}+0.10\vec{k}\right)\frac{\mathrm{m}}{\mathrm{s}^2}

3.2 Aceleración normal

3.2.1 A partir de su expresión vectorial

La parte normal de la aceleración en un movimiento circular es

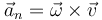
\vec{a}_n=\vec{\omega}\times\vec{v}

lo que en este caso da

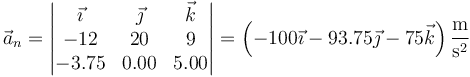
\vec{a}_n=\left|\begin{matrix}\vec{\imath} & \vec{\jmath} & \vec{k} \\ -12 & 20 & 9 \\ -3.75 & 0.00 & 5.00\end{matrix}\right| = \left(-100\vec{\imath}-93.75\vec{\jmath}-75\vec{k}\right)\frac{\mathrm{m}}{\mathrm{s}^2}

y en forma escalar

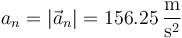
a_n=\left|\vec{a}_n\right| = 156.25\,\frac{\mathrm{m}}{\mathrm{s}^2}

3.2.2 A partir de su módulo, dirección y sentido

La aceleración normal en este movimiento puede también calcularse observando que:

  • Tiene por módulo
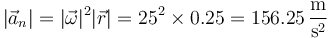
|\vec{a}_n| = |\vec{\omega}|^2|\vec{r}|=25^2\times 0.25= 156.25\,\frac{\mathrm{m}}{\mathrm{s}^2}
  • Su dirección es radial, es decir en la de
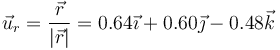
\vec{u}_r=\frac{\vec{r}}{|\vec{r}|}=0.64\vec{\imath}+0.60\vec{\jmath}-0.48\vec{k}
  • Su sentido es hacia adentro de la circunferencia, según el vector normal
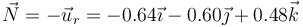
\vec{N}=-\vec{u}_r = -0.64\vec{\imath}-0.60\vec{\jmath}+0.48\vec{k}

Todo esto da

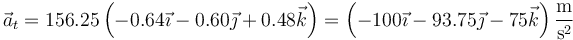
\vec{a}_t=156.25\left(-0.64\vec{\imath}-0.60\vec{\jmath}+0.48\vec{k}\right)=\left(-100\vec{\imath}-93.75\vec{\jmath}-75\vec{k}\right)\frac{\mathrm{m}}{\mathrm{s}^2}

y la forma escalar

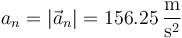
a_n=\left|\vec{a}_n\right| = 156.25\,\frac{\mathrm{m}}{\mathrm{s}^2}

4 Vectores tangente y normal

4.1 Vector tangente

El vector tangente es el unitario en la dirección y sentido de la velocidad

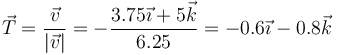
\vec{T}=\frac{\vec{v}}{|\vec{v}|}=-\frac{3.75\vec{\imath}+5\vec{k}}{6.25}=-0.6\vec{\imath}-0.8\vec{k}

4.2 Vector normal

El vector normal es el unitario en la dirección y sentido de la aceleración normal

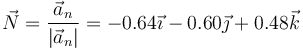
\vec{N}=\frac{\vec{a}_n}{|\vec{a}_n|}= -0.64\vec{\imath}-0.60\vec{\jmath}+0.48\vec{k}

que en el caso de un movimiento circular alrededor del origen es radial y hacia el centro de la circunferencia

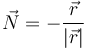
\vec{N}=-\frac{\vec{r}}{|\vec{r}|}

5 Radio y centro de curvatura

El radio de curvatura puede hallarse por la fórmula

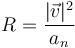
R=\frac{|\vec{v}|^2}{a_n}

pero en el caso de un movimiento circular alrededor del origen es simplemente la distancia a éste

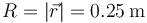
R=|\vec{r}| = 0.25\,\mathrm{m}

El centro de curvatura se puede hallar por

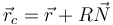
\vec{r}_c=\vec{r}+R\vec{N}

pero en el caso de un movimiento circular el centro de curvatura es el propio centro de la circunferencia, que en este caso es

\vec{r}_c=\vec{0}
Obtenido de "http://tesla.us.es/wiki/index.php/Rotaci%C3%B3n_tridimensional_de_una_part%C3%ADcula"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Esta página fue modificada por última vez el 19:47, 4 nov 2014. - Esta página ha sido visitada 3.711 veces. - Aviso legal - Acerca de Laplace