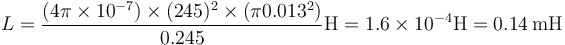Comportamiento de una bobina real
De Laplace
(Diferencias entre revisiones)
(Página creada con '==Enunciado== Con 20 m de hilo de cobre de 1 mm de diámetro se construye una bobina, arrollándola sobre un cilindro de cartón de 26 mm de diámetro. El h…') |
|||
| Línea 7: | Línea 7: | ||
# Suponga que la bobina se conecta a la fuente anterior empleando un interruptor que se cierra en <math>t=0</math>. ¿Cuánto tiempo tarda aproximadamente en establecerse la corriente continua? | # Suponga que la bobina se conecta a la fuente anterior empleando un interruptor que se cierra en <math>t=0</math>. ¿Cuánto tiempo tarda aproximadamente en establecerse la corriente continua? | ||
==Resistencia== | ==Resistencia== | ||
| + | La resistencia de un hilo metálico es | ||
| + | |||
| + | <center><math>R=\frac{l}{\sigma A}</math></center> | ||
| + | |||
| + | siendo A la sección transversal | ||
| + | |||
| + | <center><math>A = \frac{\pi d^2}{4}=7.85\times 10^{-7}\mathrm{m}^2</math></center> | ||
| + | |||
| + | lo que da la resistencia | ||
| + | |||
| + | <center><math>R = \frac{20}{5.96\times 10^7 \times 7.85\times 10^{-7}}\Omega = 0.427\,\Omega</math></center> | ||
| + | |||
==Coeficiente de autoinducción== | ==Coeficiente de autoinducción== | ||
| + | Cuando se construye un solenoide largo, su coeficiente de autoinducción vale | ||
| + | |||
| + | <center><math>L=\frac{\mu_0N^2\pi a^2}{h}</math></center> | ||
| + | |||
| + | siendo <math>a</math> el radio del solenoid | ||
| + | |||
| + | <center><math>a = \frac{D}{2}=13\,\mathrm{mm}=0.013\,\mathrm{m}</math></center> | ||
| + | |||
| + | <math>N</math> es el número de vueltas. Esto lo obtenemos de que cada vuelta mide <math>2\pi a</math>, por lo que el número de vueltas que podemos conseguir con 20m de cable es | ||
| + | |||
| + | <center><math>N = \frac{l}{2\pi a}=245\,\mathrm{vueltas}</math></center> | ||
| + | |||
| + | <math>h</math> es la altura de la bobina. Si tenemos N vueltas densamente apiladas, la altura total es igual a N veces el diámetro del hilo | ||
| + | |||
| + | <center><math>h = Nd = 0.245\,\mathrm{m}</math></center> | ||
| + | |||
| + | Todo esto nos da el coeficiente | ||
| + | |||
| + | <center><math>L = \frac{(4\pi\times 10^{-7})\times (245)^2\times (\pi 0.013^2)}{0.245}\mathrm{H}=1.6\times 10^{-4}\mathrm{H}=0.14\,\mathrm{mH}</math></center> | ||
| + | |||
==Campo magnético== | ==Campo magnético== | ||
==Comportamiento transitorio== | ==Comportamiento transitorio== | ||
[[Categoría:Problemas de inducción electromagnética (GIE)]] | [[Categoría:Problemas de inducción electromagnética (GIE)]] | ||
Revisión de 17:23 13 jun 2014
Contenido |
1 Enunciado
Con 20 m de hilo de cobre de 1 mm de diámetro se construye una bobina, arrollándola sobre un cilindro de cartón de 26 mm de diámetro. El hilo se enrolla densamente, sin dejar espacio entre vuelta y vuelta.
- Halle la resistencia de la bobina (conductividad del cobre:
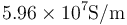 ).
).
- Calcule el coeficiente de autoinducción de la bobina.
- Suponga que se conecta la bobina a una fuente de continua de 1 V. ¿Qué campo magnético produce esta bobina en su interior?
- Suponga que la bobina se conecta a la fuente anterior empleando un interruptor que se cierra en t = 0. ¿Cuánto tiempo tarda aproximadamente en establecerse la corriente continua?
2 Resistencia
La resistencia de un hilo metálico es

siendo A la sección transversal
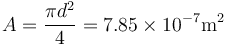
lo que da la resistencia
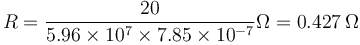
3 Coeficiente de autoinducción
Cuando se construye un solenoide largo, su coeficiente de autoinducción vale
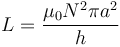
siendo a el radio del solenoid
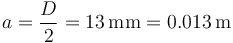
N es el número de vueltas. Esto lo obtenemos de que cada vuelta mide 2πa, por lo que el número de vueltas que podemos conseguir con 20m de cable es
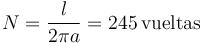
h es la altura de la bobina. Si tenemos N vueltas densamente apiladas, la altura total es igual a N veces el diámetro del hilo
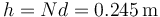
Todo esto nos da el coeficiente