Comportamiento de una bobina real

De Laplace

Contenido

1 Enunciado
2 Resistencia
3 Coeficiente de autoinducción
4 Campo magnético
5 Comportamiento transitorio

1 Enunciado

Con 20 m de hilo de cobre de 1 mm de diámetro se construye una bobina, arrollándola sobre un cilindro de cartón de 26 mm de diámetro. El hilo se enrolla densamente, sin dejar espacio entre vuelta y vuelta.

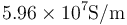Halle la resistencia de la bobina (conductividad del cobre: $5.96\times 10^{7}\mathrm{S}/\mathrm{m}$ ).
Calcule el coeficiente de autoinducción de la bobina.
Suponga que se conecta la bobina a una fuente de continua de 1 V. ¿Qué campo magnético produce esta bobina en su interior?
Suponga que la bobina se conecta a la fuente anterior empleando un interruptor que se cierra en $t = 0$ . ¿Cuánto tiempo tarda aproximadamente en establecerse la corriente continua?

2 Resistencia

La resistencia de un hilo metálico es

$R=\frac{l}{\sigma A}$

siendo A la sección transversal

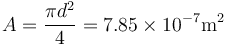
$A = \frac{\pi d^2}{4}=7.85\times 10^{-7}\mathrm{m}^2$

lo que da la resistencia

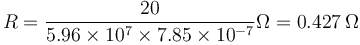
$R = \frac{20}{5.96\times 10^7 \times 7.85\times 10^{-7}}\Omega = 0.427\,\Omega$

3 Coeficiente de autoinducción

Cuando se construye un solenoide largo, su coeficiente de autoinducción vale

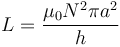
$L=\frac{\mu_0N^2\pi a^2}{h}$

siendo $a$ el radio del solenoid

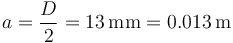
$a = \frac{D}{2}=13\,\mathrm{mm}=0.013\,\mathrm{m}$

$N$ es el número de vueltas. Esto lo obtenemos de que cada vuelta mide $2π a$ , por lo que el número de vueltas que podemos conseguir con 20m de cable es

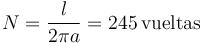
$N = \frac{l}{2\pi a}=245\,\mathrm{vueltas}$

$h$ es la altura de la bobina. Si tenemos N vueltas densamente apiladas, la altura total es igual a N veces el diámetro del hilo

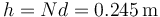
$h = Nd = 0.245\,\mathrm{m}$

Todo esto nos da el coeficiente

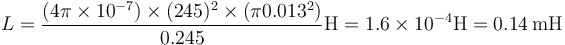
$L = \frac{(4\pi\times 10^{-7})\times (245)^2\times (\pi 0.013^2)}{0.245}\mathrm{H}=1.6\times 10^{-4}\mathrm{H}=0.14\,\mathrm{mH}$

4 Campo magnético

El campo magnético producido por un solenoide largo, como este, en su interior vale aproximadamente

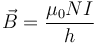
$\vec{B}=\frac{\mu_0 N I}{h}$

donde la corriente la hallamos a partir de la ley de Ohm

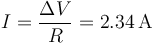
$I = \frac{\Delta V}{R}=2.34\,\mathrm{A}$

lo que da el campo magnético

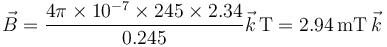
$\vec{B}=\frac{4\pi\times 10^{-7}\times 245\times 2.34}{0.245}\vec{k}\,\mathrm{T}=2.94\,\mathrm{mT}\,\vec{k}$

5 Comportamiento transitorio

Cuando el voltaje aplicado no es una función continua, sino una función escalón

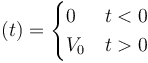
$\mathcal(t)=\begin{cases} 0 & t < 0 \\ V_0 & t>0\end{cases}$

Debemos resolver la ecuación diferencial para la corriente en un circuito con resistencia y autoinducción

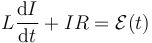
$L\frac{\mathrm{d}I}{\mathrm{d}t}+IR=\mathcal{E}(t)$

La solución de esta ecuación diferencial es

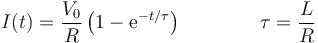
$I(t) = \frac{V_0}{R}\left(1-\mathrm{e}^{-t/\tau}\right)\qquad\qquad \tau=\frac{L}{R}$

que nos dice que la corriente tiende asintóticamente al valor estacionario calculado en el apartado anterior, pero necesita un cierto tiempo para hacerlo. El tiempo típico en que tarda en establecerse la corriente continua vale

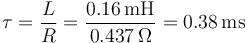
$\tau = \frac{L}{R}=\frac{0.16\,\mathrm{mH}}{0.437\,\Omega}=0.38\,\mathrm{ms}$

Como vemos se tarda un tiempo del orden de un milisegundo en establecerse la corriente.

Comportamiento de una bobina real

De Laplace

Contenido

1 Enunciado

2 Resistencia

3 Coeficiente de autoinducción

4 Campo magnético

5 Comportamiento transitorio

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES