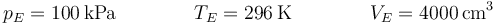Cuatro procesos no cuasiestáticos
De Laplace
| Línea 28: | Línea 28: | ||
:'''b.2''' Halle el trabajo y el calor netos que entran en el sistema, así como la variación de energía interna, en los pasos A→D y D→E. | :'''b.2''' Halle el trabajo y el calor netos que entran en el sistema, así como la variación de energía interna, en los pasos A→D y D→E. | ||
:'''b.3''' Halle la variación de entropía del sistema, del ambiente y del universo en cada uno de los dos pasos. | :'''b.3''' Halle la variación de entropía del sistema, del ambiente y del universo en cada uno de los dos pasos. | ||
| + | ==Presiones, volúmenes y temperaturas== | ||
| + | Comenzamos anotando los datos que conocemos e iremos rellenando los que podamos deducir de estos empleando la ley de los gases ideales y el conocimiento de los diferentes procesos. | ||
| + | |||
| + | Del estado inicial '''A''' tenemos toda la información | ||
| + | |||
| + | <center><math>p_A=450\,\mathrm{kPa}\qquad\qquad V_A=1000\,\mathrm{cm}^3\qquad\qquad T_A=333\,\mathrm{K}</math></center> | ||
| + | |||
| + | En el estado final '''C''', el gas tiene la temperatura y la presión del ambiente, ya que ha alcanzado el equilibrio térmico y mecánico. | ||
| + | |||
| + | <center><math>p_C=100\,\mathrm{kPa}\qquad\qquad T_C=296\,\mathrm{K}</math></center> | ||
| + | |||
| + | Mediante la ley de los gases ideales calculamos el volumen en el estado final C | ||
| + | |||
| + | <center><math>\frac{p_CV_C}{T_C}=\frac{p_AV_A}{T_A}\qquad\Rightarrow\qquad V_C=\frac{T_Cp_A}{T_Ap_C}V_A=\frac{296\times 450}{333\times 100}\times 1000\,\mathrm{cm}^3=4000\,\mathrm{cm}^3</math></center> | ||
| + | |||
| + | El estado E es exactamente el mismo que el C: de equilibrio mecánico y térmico con el ambiente. Por ello: | ||
| + | |||
| + | <center><math>p_E=100\,\mathrm{kPa}\qquad\qquad T_E=296\,\mathrm{K}\qquad\qquad V_E=4000\,\mathrm{cm}^3</math></center> | ||
Revisión de 18:03 8 abr 2014
1 Enunciado
Se tiene un cilindro horizontal cerrado por un pistón, en cuyo interior hay aire seco (considerado un gas ideal diatómico). Inicialmente, el aire interior se encuentra a 450 kPa y 333 K, ocupando un volumen de 1000 cm³. El ambiente se encuentra a 100 kPa y 296 K, valores que no cambian en ningún momento.
Las paredes del cilindro son adiabáticas. El pistón está inicialmente limitado por un tope y forrado de forma que está aislado térmicamente.
Se realiza entonces el siguiente proceso compuesto:
- A→B Se libera bruscamente el tope, dejando que el gas se expanda sin quitarle el aislante térmico.
- B→C Una vez que se ha alcanzado de nuevo el equilibrio y sin volver a fijar la tapa, se quita bruscamente el aislante térmico, dejando que el sistema evolucione.
Ninguno de los dos pasos es cuasiestático.
Para este proceso
- a.1 Calcule la presión, volumen y temperatura del gas en los estados B y C.
- a.2 Halle el trabajo y el calor netos que entran en el sistema, así como la variación de energía interna, en los pasos A→B y B→C.
- a.3 Halle la variación de entropía del sistema, del ambiente y del universo en cada uno de los dos pasos.
Suponga ahora que, partiendo del mismo estado inicial se realizan los dos desbloqueos en orden inverso, es decir,
- A→D Se quita bruscamente el aislante térmico, sin quitar el tope
- D→E Sin volver a poner el aislante, se libera bruscamente el tope.
Ninguno de los dos pasos es cuasiestático.
Para este nuevo proceso, calcule las mismas magnitudes que en el caso anterior, es decir:
- b.1 Calcule la presión, volumen y temperatura del gas en los estados D y E.
- b.2 Halle el trabajo y el calor netos que entran en el sistema, así como la variación de energía interna, en los pasos A→D y D→E.
- b.3 Halle la variación de entropía del sistema, del ambiente y del universo en cada uno de los dos pasos.
2 Presiones, volúmenes y temperaturas
Comenzamos anotando los datos que conocemos e iremos rellenando los que podamos deducir de estos empleando la ley de los gases ideales y el conocimiento de los diferentes procesos.
Del estado inicial A tenemos toda la información
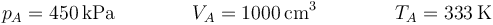
En el estado final C, el gas tiene la temperatura y la presión del ambiente, ya que ha alcanzado el equilibrio térmico y mecánico.

Mediante la ley de los gases ideales calculamos el volumen en el estado final C
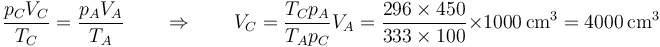
El estado E es exactamente el mismo que el C: de equilibrio mecánico y térmico con el ambiente. Por ello: