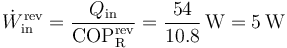Consumo de un refrigerador
De Laplace
| Línea 20: | Línea 20: | ||
lo que nos da | lo que nos da | ||
| - | <center><math>\dot{Q}=-0.04\times 2.16\times\frac{25}{0.04}\mathrm{W}=54\,\mathrm{W}</math></center> | + | <center><math>\dot{Q}=-0.04\times 2.16\times\frac{(-25)}{0.04}\mathrm{W}=+54\,\mathrm{W}</math></center> |
| + | |||
| + | Resulta un calor positivo, ya que va hacia el interior del congelador. | ||
==Trabajo mínimo== | ==Trabajo mínimo== | ||
| + | El trabajo mínimo se obtiene suponiendo que el refrigerador es uno reversible, cuyo coeficiente de desempeño vale | ||
| + | |||
| + | <center><math>\mathrm{COP}^\mathrm{rev}_\mathrm{R}=\frac{T_F}{T_C-T_F}=\frac{270}{25}=10.8</math></center> | ||
| + | |||
| + | lo que nos da un trabajo mínimo por segundo | ||
| + | |||
| + | <center><math>\dot{W}^\mathrm{rev}_\mathrm{in}=\frac{Q_\mathrm{in}}{\mathrm{COP}^\mathrm{rev}_\mathrm{R}}=\frac{54}{10.8}\,\mathrm{W}=5\,\mathrm{W}</math></center> | ||
==Producción de entropía== | ==Producción de entropía== | ||
==Trabajo para fabricar cubitos== | ==Trabajo para fabricar cubitos== | ||
[[Categoría:Problemas de máquinas térmicas (GIE)]] | [[Categoría:Problemas de máquinas térmicas (GIE)]] | ||
[[Categoría:Problemas del segundo principio de la termodinámica (GIE)]] | [[Categoría:Problemas del segundo principio de la termodinámica (GIE)]] | ||
Revisión de 19:03 26 mar 2014
Contenido |
1 Enunciado
Se tiene un congelador en forma de cubo de 60 cm×60 cm×60 cm cuyas paredes son de fibra de vidrio de 4 cm de grosor. La temperatura interior del congelador es −3 °C y la exterior es de +22 °C
- ¿Cuánto vale aproximadamente el calor que entra en el congelador por segundo?
- ¿Cuál es el trabajo por segundo mínimo necesario para hacer funcionar este congelador y mantener constante la temperatura interior?
- Suponga que la potencia real necesaria para hacerlo funcionar es de 123 W. ¿Cuánto es la producción de entropía por segundo en el universo debida a este refrigerador?
- Suponga que se introduce en el congelador una cubitera con 200 g de agua a temperatura ambiente. ¿Cuánto trabajo debe introducirse en el congelador para fabricar los cubitos?
Datos: Conductividad térmica de la fibra de vidrio: 0.04 W/(m·K); Calor específico del agua: 4.18 kJ/(kg·K); Calor específico del hielo: 2.09 kJ/(kg·K); Entalpía específica de fusión del agua: 334 kJ/kg.
2 Calor que entra
Al haber una pared sólida, el calor entra en el frigorífico por conducción, cumpliéndose la ley de Fourier
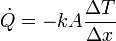
En este caso, k es la conductividad térmica de la fibra de vidrio, Δx es el espesor de la pared, ΔT es la diferencia de temperaturas entre el exterior y el interior y A es el área del cubo, que es igual a 6 veces el área de una cara, es decir
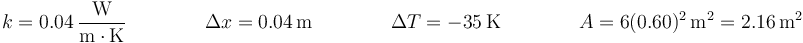
lo que nos da
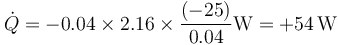
Resulta un calor positivo, ya que va hacia el interior del congelador.
3 Trabajo mínimo
El trabajo mínimo se obtiene suponiendo que el refrigerador es uno reversible, cuyo coeficiente de desempeño vale
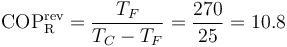
lo que nos da un trabajo mínimo por segundo