No Boletín - Dos varillas (Ex.Feb/14)
De Laplace
| Línea 9: | Línea 9: | ||
# Aceleración <math>\vec{a}^{\, C}_{21}\,</math> | # Aceleración <math>\vec{a}^{\, C}_{21}\,</math> | ||
| - | == | + | ==Caracterización de los movimientos elementales {01} y {20}== |
| + | Tanto el movimiento de arrastre {01} como el movimiento relativo {20} son rotaciones puras alrededor de sendos ejes fijos (ejes permanentes de rotación). En concreto, el EPR{01} es el eje <math>OZ_1\equiv OZ_0\,</math>, y el EPR{20} es el eje <math>OX_0\,</math>. Para caracterizar estos dos movimientos elementales, vamos a determinar sus reducciones cinemáticas en el punto donde se cortan sus respectivos ejes de rotación (punto <math>O\,</math>). | ||
| + | |||
| + | Las velocidades de arrastre <math>\vec{v}^{\, O}_{01}\,</math> y relativa <math>\vec{v}^{\, O}_{20}\,</math> son nulas por ser el punto <math>O\,</math> un punto fijo en ambos movimientos. Y los vectores velocidad angular <math>\vec{\omega}_{01}\,</math> y <math>\vec{\omega}_{20}\,</math> se deducen del enunciado (sus direcciones son las de los correspondientes ejes de rotación, sus módulos son las constantes especificadas, y sus sentidos son los indicados en la figura). Así pues, las reducciones cinemáticas de los movimientos {01} y {20} en el punto <math>O\,</math> son: | ||
| + | <center><math> | ||
| + | \left\{\begin{array}{l} \vec{\omega}_{01}(t)=\omega\,\vec{k}_0 \\ \\ \vec{v}^{\, O}_{01}(t)=\vec{0} \end{array}\right.\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \left\{\begin{array}{l} \vec{\omega}_{20}(t)=-\Omega\,\vec{\imath}_0 \\ \\ \vec{v}^{\, O}_{20}(t)=\vec{0} \end{array}\right. | ||
| + | </math></center> | ||
| + | Con vistas al cálculo de aceleraciones, resulta interesante determinar también las aceleraciones angulares y las aceleraciones del punto <math>O\,</math> en los movimientos de arrastre y relativo: | ||
| + | <center><math> | ||
| + | \left|\begin{array}{l} \vec{\alpha}_{01}=\displaystyle\left.\frac{\mathrm{d}\vec{\omega}_{01}}{\mathrm{d}t}\right|_1=\displaystyle\left.\frac{\mathrm{d}(\omega\,\vec{k}_1)}{\mathrm{d}t}\right|_1=\vec{0} \\ \\ \vec{a}^{\, O}_{01}=\displaystyle\left.\frac{\mathrm{d}\vec{v}^{\, O}_{01}}{\mathrm{d}t}\right|_1=\displaystyle\left.\frac{\mathrm{d}\vec{0}}{\mathrm{d}t}\right|_1=\vec{0} \end{array}\right.\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \left|\begin{array}{l} \vec{\alpha}_{20}=\displaystyle\left.\frac{\mathrm{d}\vec{\omega}_{20}}{\mathrm{d}t}\right|_0=\displaystyle\left.\frac{\mathrm{d}(-\Omega\,\vec{\imath}_0)}{\mathrm{d}t}\right|_0=\vec{0} \\ \\ \vec{a}^{\, O}_{20}=\displaystyle\left.\frac{\mathrm{d}\vec{v}^{\, O}_{20}}{\mathrm{d}t}\right|_0=\displaystyle\left.\frac{\mathrm{d}\vec{0}}{\mathrm{d}t}\right|_0=\vec{0} \end{array}\right. | ||
| + | </math></center> | ||
| + | |||
| + | ==Aceleración angular {21}== | ||
| + | Determinamos <math>\vec{\alpha}_{21}\,</math> aplicando la ley de composición de aceleraciones angulares: | ||
| + | <center><math> | ||
| + | \vec{\alpha}_{21}=\underbrace{\vec{\alpha}_{20}}_{\vec{0}}+\underbrace{\vec{\alpha}_{01}}_{\vec{0}}+\,\,\vec{\omega}_{01}\times\vec{\omega}_{20}=\omega\,\vec{k}_0\times (-\Omega\,\vec{\imath}_0)=-\Omega\,\omega\,\vec{\jmath}_0 | ||
| + | </math></center> | ||
| + | |||
| + | ==Velocidad instantánea {21} del punto A== | ||
| + | Para determinar la velocidad absoluta <math>\vec{v}^{\, A}_{21}\,</math>, calculamos primero las velocidades relativa <math>\vec{v}^{\, A}_{20}\,</math> y de arrastre <math>\vec{v}^{\, A}_{01}\,</math> utilizando las ecuaciones de los campos de velocidades correspondientes: | ||
| + | <center><math> | ||
| + | \begin{array}{l} | ||
| + | \vec{v}^{\, A}_{20}=\displaystyle\underbrace{\vec{v}^{\, O}_{20}}_{\vec{0}}+\,\,\vec{\omega}_{20}\times\overrightarrow{OA}=-\Omega\,\vec{\imath}_0\times R\,\vec{\jmath}_0=-\Omega R\,\vec{k}_0 \\ \\ | ||
| + | \vec{v}^{\, A}_{01}=\displaystyle\underbrace{\vec{v}^{\, O}_{01}}_{\vec{0}}+\,\,\vec{\omega}_{01}\times\overrightarrow{OA}=\omega\,\vec{k}_0\times R\,\vec{\jmath}_0=-\omega R\,\vec{\imath}_0 | ||
| + | \end{array} | ||
| + | </math></center> | ||
| + | y, a continuación, aplicamos la ley de composición de velocidades: | ||
| + | <center><math> | ||
| + | \vec{v}^{\, A}_{21}=\vec{v}^{\, A}_{20}+\vec{v}^{\, A}_{01}=-R\,(\omega\,\vec{\imath}_0+\Omega\,\vec{k}_0) | ||
| + | </math></center> | ||
| + | |||
| + | ==Aceleración instantánea {21} del punto B== | ||
| + | Conforme a la ley de composición de aceleraciones (teorema de Coriolis), la aceleración absoluta <math>\vec{a}^{\, B}_{21}\,</math> se calcula así: | ||
| + | <center><math> | ||
| + | \vec{a}^{\, B}_{21}=\vec{a}^{\, B}_{20}+\vec{a}^{\, B}_{01}+2\,\vec{\omega}_{01}\times\vec{v}^{\, B}_{20} | ||
| + | </math></center> | ||
| + | Necesitamos, por tanto, calcular previamente la aceleración relativa <math>\vec{a}^{\, B}_{20}\,</math> (mediante la ecuación del campo de aceleraciones {20}): | ||
| + | <center><math> | ||
| + | \vec{a}^{\, B}_{20}=\underbrace{\vec{a}^{\, O}_{20}}_{\vec{0}}+\,\underbrace{\vec{\alpha}_{20}}_{\vec{0}}\times\,\overrightarrow{OB}\,+\,\vec{\omega}_{20}\times(\omega_{20}\times\overrightarrow{OB})=-\Omega\,\vec{\imath}_0\times(-\Omega\,\vec{\imath}_0\times R\,\vec{k}_0)=-\Omega^2 R\,\vec{k}_0 | ||
| + | </math></center> | ||
| + | la aceleración de arrastre <math>\vec{a}^{\, B}_{01}\,</math> (la cual es nula por pertenecer el punto <math>B\,</math> al EPR{01}, es decir, por ser <math>B\,</math> un punto fijo en el movimiento {01}): | ||
| + | <center><math> | ||
| + | \vec{a}^{\, B}_{01}=\vec{0} | ||
| + | </math></center> | ||
| + | y el término de Coriolis (mediante su fórmula): | ||
| + | <center><math> | ||
| + | 2\,\vec{\omega}_{01}\times\vec{v}^{\, B}_{20}=2\,\vec{\omega}_{01}\times(\,\underbrace{\vec{v}^{\, O}_{20}}_{\vec{0}}+\,\,\vec{\omega}_{20}\times\overrightarrow{OB})=2\,\omega\,\vec{k}_0\times(-\Omega\,\vec{\imath}_0\times R\,\vec{k}_0)=-2\,\Omega\,\omega R\,\vec{\imath}_0 | ||
| + | </math></center> | ||
| + | Sustituyendo en la ley de composición de aceleraciones, obtenemos por fin la aceleración absoluta <math>\vec{a}^{\, B}_{21}\,</math>: | ||
| + | <center><math> | ||
| + | \vec{a}^{\, B}_{21}=\!\!\underbrace{\vec{a}^{\, B}_{20}}_{-\Omega^2 R\,\vec{k}_0}\!\!\!+\underbrace{\vec{a}^{\, B}_{01}}_{\vec{0}}+\,\underbrace{2\,\vec{\omega}_{01}\!\times\vec{v}^{\, B}_{20}}_{-2\,\Omega\,\omega R\,\vec{\imath}_0}=-\Omega R\,(2\,\omega\,\vec{\imath}_0+\Omega\,\vec{k}_0) | ||
| + | </math></center> | ||
| + | |||
| + | ==Procedimiento alternativo== | ||
| + | Podemos utilizar un procedimiento alternativo, el cual consiste en determinar primero la velocidad angular y la aceleración angular del movimiento {21}, así como la velocidad y la aceleración de un punto arbitrario en el movimiento {21}, y -a partir de estas cuatro magnitudes- calcular posteriormente las otras magnitudes {21} que se nos piden. La única ley de composición que utilizaremos con este procedimiento es la de velocidades angulares. | ||
| + | |||
| + | Al ser los movimientos {01} y {20} rotaciones concurrentes (el EPR{01} y el EPR{20} se cortan en el punto <math>O\,</math>), sabemos que su composición (el movimiento {21}) es otra rotación cuyo eje también pasa por el punto de concurrencia. Quiere esto decir que el punto <math>O\,</math> pertenece permanentemente al EIR{21} y, por tanto, es un punto fijo en el movimiento {21}. Así que ya tenemos la velocidad y la aceleración de un punto en el movimiento {21} para todo instante de tiempo: | ||
| + | <center><math> | ||
| + | \vec{v}^{\, O}_{21}(t)=\vec{0}\,\,;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\vec{a}^{\, O}_{21}(t)=\vec{0} | ||
| + | </math></center> | ||
| + | Por otra parte, podemos calcular la velocidad angular del movimiento {21} mediante la correspondiente ley de composición: | ||
| + | <center><math> | ||
| + | \vec{\omega}_{21}(t)=\vec{\omega}_{20}(t)+\vec{\omega}_{01}(t)=-\Omega\,\vec{\imath}_0+\omega\,\vec{k}_0 | ||
| + | </math></center> | ||
| + | y, derivándola respecto al tiempo (con ayuda de la fórmula de Poisson), obtenemos la aceleración angular del movimiento {21}: | ||
| + | <center><math> | ||
| + | \vec{\alpha}_{21}=\left.\frac{\mathrm{d}\vec{\omega}_{21}}{\mathrm{d}t}\right|_1=\left.\frac{\mathrm{d}\vec{\omega}_{21}}{\mathrm{d}t}\right|_0+\,\,\vec{\omega}_{01}\times\,\vec{\omega}_{21}=\underbrace{\left.\frac{\mathrm{d}(-\Omega\,\vec{\imath}_0+\omega\,\vec{k}_0)}{\mathrm{d}t}\right|_0}_{\vec{0}}+\,\,\omega\,\vec{k}_0\,\times\,(-\Omega\,\vec{\imath}_0\,+\,\,\omega\,\vec{k}_0)=-\Omega\,\omega\,\vec{\jmath}_0 | ||
| + | </math></center> | ||
| + | Y, por último, determinamos <math>\vec{v}^{\, A}_{21}\,</math> y <math>\vec{a}^{\, B}_{21}\,</math> utilizando, respectivamente, las ecuaciones del campo de velocidades y del campo de aceleraciones del movimiento {21}: | ||
| + | <center><math> | ||
| + | \begin{array}{l} | ||
| + | \vec{v}^{\, A}_{21}=\displaystyle\underbrace{\vec{v}^{\, O}_{21}}_{\vec{0}}+\,\,\vec{\omega}_{21}\times\overrightarrow{OA}=(-\Omega\,\vec{\imath}_0+\omega\,\vec{k}_0)\times R\,\vec{\jmath}_0=-R\,(\omega\,\vec{\imath}_0+\Omega\,\vec{k}_0) \\ \\ | ||
| + | \vec{a}^{\, B}_{21}=\underbrace{\vec{a}^{\, O}_{21}}_{\vec{0}}+\,\,\vec{\alpha}_{21}\times\,\overrightarrow{OB}\,+\,\vec{\omega}_{21}\times(\omega_{21}\times\overrightarrow{OB})=-\Omega\,\omega\,\vec{\jmath}_0\times R\,\vec{k}_0\,+\,(-\Omega\,\vec{\imath}_0+\omega\,\vec{k}_0)\times[(-\Omega\,\vec{\imath}_0+\omega\,\vec{k}_0)\times\,R\,\vec{k}_0]=-\Omega R\,(2\,\omega\,\vec{\imath}_0+\Omega\,\vec{k}_0) | ||
| + | \end{array} | ||
| + | </math></center> | ||
[[Categoría:Problemas de movimiento relativo (G.I.T.I.)]] | [[Categoría:Problemas de movimiento relativo (G.I.T.I.)]] | ||
Revisión de 16:23 24 mar 2014
Contenido |
1 Enunciado
La varilla rígida 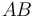 (sólido "0"), de longitud
(sólido "0"), de longitud 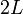 , está vinculada mediante un par cilíndrico al eje vertical
, está vinculada mediante un par cilíndrico al eje vertical 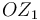 del triedro fijo
del triedro fijo 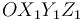 (sólido "1"), de tal forma que dicha varilla se mantiene en todo instante perpendicular al eje
(sólido "1"), de tal forma que dicha varilla se mantiene en todo instante perpendicular al eje 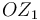 . La varilla "0" rota alrededor del eje
. La varilla "0" rota alrededor del eje 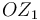 con velocidad angular constante
con velocidad angular constante 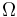 (en el sentido mostrado en la figura) y, simultáneamente, su extremo
(en el sentido mostrado en la figura) y, simultáneamente, su extremo  recorre el citado eje
recorre el citado eje 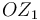 con celeridad constante
con celeridad constante 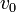 (en el sentido indicado en la figura). Por otra parte, una segunda varilla rígida
(en el sentido indicado en la figura). Por otra parte, una segunda varilla rígida 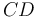 (sólido "2"), de longitud
(sólido "2"), de longitud  , se encuentra articulada mediante un par de revolución al centro
, se encuentra articulada mediante un par de revolución al centro  de la primera, de tal forma que la varilla "2" se mantiene siempre contenida en el plano perpendicular a la varilla "0" que pasa por
de la primera, de tal forma que la varilla "2" se mantiene siempre contenida en el plano perpendicular a la varilla "0" que pasa por  . El movimiento {20} viene dado por la rotación de la varilla "2" alrededor del eje de la varilla "0" (eje
. El movimiento {20} viene dado por la rotación de la varilla "2" alrededor del eje de la varilla "0" (eje 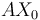 ) con velocidad angular constante
) con velocidad angular constante 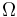 (en el sentido mostrado en la figura). Sea
(en el sentido mostrado en la figura). Sea 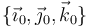 la base ortonormal asociada al triedro
la base ortonormal asociada al triedro 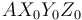 (sólido "0") que se define en la figura.
(sólido "0") que se define en la figura.
Determine las siguientes magnitudes:
- Velocidad
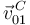
- Aceleración angular
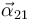
- Aceleración
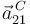
2 Caracterización de los movimientos elementales {01} y {20}
Tanto el movimiento de arrastre {01} como el movimiento relativo {20} son rotaciones puras alrededor de sendos ejes fijos (ejes permanentes de rotación). En concreto, el EPR{01} es el eje 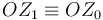 , y el EPR{20} es el eje
, y el EPR{20} es el eje 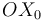 . Para caracterizar estos dos movimientos elementales, vamos a determinar sus reducciones cinemáticas en el punto donde se cortan sus respectivos ejes de rotación (punto
. Para caracterizar estos dos movimientos elementales, vamos a determinar sus reducciones cinemáticas en el punto donde se cortan sus respectivos ejes de rotación (punto  ).
).
Las velocidades de arrastre 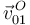 y relativa
y relativa 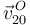 son nulas por ser el punto
son nulas por ser el punto  un punto fijo en ambos movimientos. Y los vectores velocidad angular
un punto fijo en ambos movimientos. Y los vectores velocidad angular 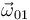 y
y 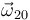 se deducen del enunciado (sus direcciones son las de los correspondientes ejes de rotación, sus módulos son las constantes especificadas, y sus sentidos son los indicados en la figura). Así pues, las reducciones cinemáticas de los movimientos {01} y {20} en el punto
se deducen del enunciado (sus direcciones son las de los correspondientes ejes de rotación, sus módulos son las constantes especificadas, y sus sentidos son los indicados en la figura). Así pues, las reducciones cinemáticas de los movimientos {01} y {20} en el punto  son:
son:

Con vistas al cálculo de aceleraciones, resulta interesante determinar también las aceleraciones angulares y las aceleraciones del punto  en los movimientos de arrastre y relativo:
en los movimientos de arrastre y relativo:
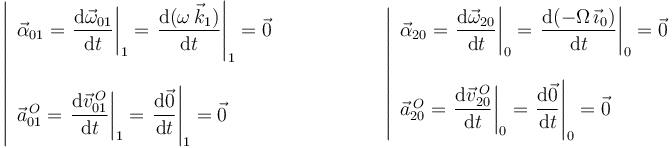
3 Aceleración angular {21}
Determinamos 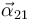 aplicando la ley de composición de aceleraciones angulares:
aplicando la ley de composición de aceleraciones angulares:
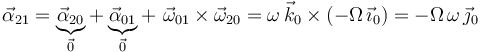
4 Velocidad instantánea {21} del punto A
Para determinar la velocidad absoluta 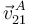 , calculamos primero las velocidades relativa
, calculamos primero las velocidades relativa 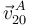 y de arrastre
y de arrastre 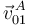 utilizando las ecuaciones de los campos de velocidades correspondientes:
utilizando las ecuaciones de los campos de velocidades correspondientes:
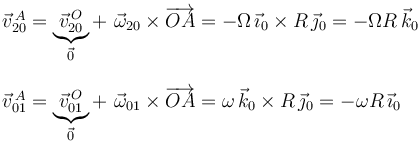
y, a continuación, aplicamos la ley de composición de velocidades:
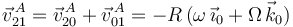
5 Aceleración instantánea {21} del punto B
Conforme a la ley de composición de aceleraciones (teorema de Coriolis), la aceleración absoluta 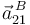 se calcula así:
se calcula así:
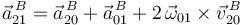
Necesitamos, por tanto, calcular previamente la aceleración relativa 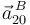 (mediante la ecuación del campo de aceleraciones {20}):
(mediante la ecuación del campo de aceleraciones {20}):
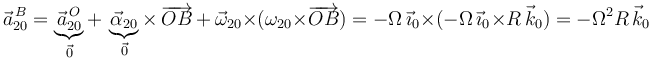
la aceleración de arrastre 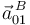 (la cual es nula por pertenecer el punto
(la cual es nula por pertenecer el punto  al EPR{01}, es decir, por ser
al EPR{01}, es decir, por ser  un punto fijo en el movimiento {01}):
un punto fijo en el movimiento {01}):
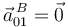
y el término de Coriolis (mediante su fórmula):
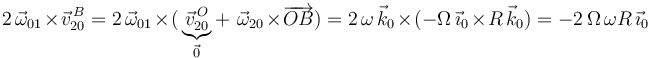
Sustituyendo en la ley de composición de aceleraciones, obtenemos por fin la aceleración absoluta 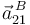 :
:
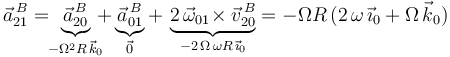
6 Procedimiento alternativo
Podemos utilizar un procedimiento alternativo, el cual consiste en determinar primero la velocidad angular y la aceleración angular del movimiento {21}, así como la velocidad y la aceleración de un punto arbitrario en el movimiento {21}, y -a partir de estas cuatro magnitudes- calcular posteriormente las otras magnitudes {21} que se nos piden. La única ley de composición que utilizaremos con este procedimiento es la de velocidades angulares.
Al ser los movimientos {01} y {20} rotaciones concurrentes (el EPR{01} y el EPR{20} se cortan en el punto  ), sabemos que su composición (el movimiento {21}) es otra rotación cuyo eje también pasa por el punto de concurrencia. Quiere esto decir que el punto
), sabemos que su composición (el movimiento {21}) es otra rotación cuyo eje también pasa por el punto de concurrencia. Quiere esto decir que el punto  pertenece permanentemente al EIR{21} y, por tanto, es un punto fijo en el movimiento {21}. Así que ya tenemos la velocidad y la aceleración de un punto en el movimiento {21} para todo instante de tiempo:
pertenece permanentemente al EIR{21} y, por tanto, es un punto fijo en el movimiento {21}. Así que ya tenemos la velocidad y la aceleración de un punto en el movimiento {21} para todo instante de tiempo:

Por otra parte, podemos calcular la velocidad angular del movimiento {21} mediante la correspondiente ley de composición:
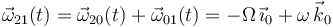
y, derivándola respecto al tiempo (con ayuda de la fórmula de Poisson), obtenemos la aceleración angular del movimiento {21}:
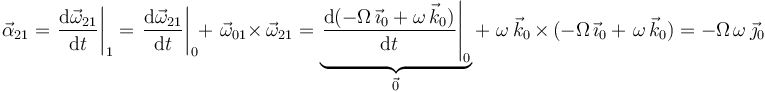
Y, por último, determinamos 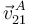 y
y 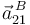 utilizando, respectivamente, las ecuaciones del campo de velocidades y del campo de aceleraciones del movimiento {21}:
utilizando, respectivamente, las ecuaciones del campo de velocidades y del campo de aceleraciones del movimiento {21}:
![\begin{array}{l}
\vec{v}^{\, A}_{21}=\displaystyle\underbrace{\vec{v}^{\, O}_{21}}_{\vec{0}}+\,\,\vec{\omega}_{21}\times\overrightarrow{OA}=(-\Omega\,\vec{\imath}_0+\omega\,\vec{k}_0)\times R\,\vec{\jmath}_0=-R\,(\omega\,\vec{\imath}_0+\Omega\,\vec{k}_0) \\ \\
\vec{a}^{\, B}_{21}=\underbrace{\vec{a}^{\, O}_{21}}_{\vec{0}}+\,\,\vec{\alpha}_{21}\times\,\overrightarrow{OB}\,+\,\vec{\omega}_{21}\times(\omega_{21}\times\overrightarrow{OB})=-\Omega\,\omega\,\vec{\jmath}_0\times R\,\vec{k}_0\,+\,(-\Omega\,\vec{\imath}_0+\omega\,\vec{k}_0)\times[(-\Omega\,\vec{\imath}_0+\omega\,\vec{k}_0)\times\,R\,\vec{k}_0]=-\Omega R\,(2\,\omega\,\vec{\imath}_0+\Omega\,\vec{k}_0)
\end{array}](/wiki/images/math/7/9/6/7967c06b4368687c249de794ffebce7b.png)






