Entrar Página Discusión Historial Go to the site toolbox

Esfera conductora con dos huecos esféricos

De Laplace

(Diferencias entre revisiones)
(→Solución)
(→Solución)
Línea 5: Línea 5:
==Solución==
==Solución==
 +
===Coeficientes de capacidad===
El problema se reduce a la determinación de los coeficientes de capacidad del sistema. Conocidos éstos, con los datos del problema pueden determinarse las cargas y potenciales restantes.  
El problema se reduce a la determinación de los coeficientes de capacidad del sistema. Conocidos éstos, con los datos del problema pueden determinarse las cargas y potenciales restantes.  
Línea 60: Línea 61:
En forma matricial
En forma matricial
-
<center><math>\begin{pmatrix}Q_1 \\ Q_2 \\ Q_3\end{pmatrix} = 2\pi\varepsilon_0\begin{pmatrix}1 & -1 & 0 \\ -1 & 4 & -1 \\ 0 & -1 & 1\end{pmatrix}\cdot\begin{pmatrix}V_1 \\ V_2 \\ V_3\end{pmatrix}</math></center>
+
<center><math>\begin{pmatrix}Q_1 \\ Q_2 \\ Q_3\end{pmatrix} = 2\pi\varepsilon_0R\begin{pmatrix}1 & -1 & 0 \\ -1 & 4 & -1 \\ 0 & -1 & 1\end{pmatrix}\cdot\begin{pmatrix}V_1 \\ V_2 \\ V_3\end{pmatrix}</math></center>
-
En nuestro problema, los datos son
+
===Cargas y voltajes===
-
\[
+
En nuestro problema, los datos son
-
Q_1=0\qquad V_2=V_0\qquad V_3=0
+
-
\]
+
-
y esto nos da
+
-
\[
+
-
0=2\pi\varepsilon_0 R(4V_1-V_0)\quad\Rightarrow\quad V_1=\frac{V_0}{4}
+
-
%\]\[
+
-
\quad Q_2=2\pi\varepsilon_0 R\left(V_0-\frac{V_0}{4}\right)=\frac{3\pi\varepsilon_0 R }{2}V_0
+
-
%\]\[
+
-
\quad Q_3=2\pi\varepsilon_0 R\left(0-\frac{V_0}{4}\right)=-\frac{\pi\varepsilon_0 R }{2}V_0
+
-
\]
+
-
y ya están determinadas todas las incógnitas del problema.
+
-
Como alternativa, aprovechando el circuito equivalente al máximo,
+
<center><math>V_1=V_0</math>{{qquad}}{{qquad}}<math>Q_2=0</math>{{qquad}}{{qquad}}<math>V_3=0</math></center>
-
podemos emplearlo para determinar las cargas en los distintos
+
-
conductores observando que, por estar los condensadores
+
-
$\overline{C}_{11}$ y $\overline{C}_{13}$ conectados al conductor 1 y a
+
-
tierra se encuentran en paralelo, formando un solo condensador de
+
-
capacidad
+
-
\dibujops{cap2-16}
+
-
\[
+
-
C=2\pi\varepsilon_0 R+4\pi\varepsilon_0 R=6\pi\varepsilon_0 R
+
-
\]
+
-
Este condensador se encuentra en serie con el $\overline{C}_{12}$. La
+
-
asociación tiene una capacidad
+
-
\[
+
-
C_\mathrm{eq}=\frac{\overline{C}_{12}C}{C+\overline{C}_{12}}=\frac{3}{2}\pi\varepsilon_0
+
-
R
+
-
\]
+
-
Como la asociación está sometida a una tensión $V_0$, la carga en la
+
-
placa positiva (el conductor 2) vale
+
-
\[
+
-
Q_2=C_\mathrm{eq}V_0=\frac{3\pi\varepsilon_0 R}{2}V_0
+
-
\]
+
-
A partir de aquí podemos calcular la tensión en el conductor 1,
+
-
restando la caída de tensión en el condensador $\overline{C}_{12}$
+
-
%\hspace*{3.8cm}
+
-
\[
+
-
V_1=V_0-\frac{Q_2}{\overline{C}_{12}}=V_0-\frac{3}{4}V_0=\frac{V_0}{4}
+
-
\]
+
-
La carga del conductor 3 la calculamos aplicando que equivale a la de
+
-
la placa negativa del condensador $\overline{C}_{13}$, sometido a una
+
-
tensión $V_0/4$
+
-
\[
+
-
Q_3=-\overline{C}_{13}\frac{V_0}{4}=-\frac{\pi\varepsilon_0 R}{2}V_0
+
-
\]
+
-
\rule{1cm}{0cm}%resultando los valores ya conocidos.
+
-
Para hallar la energía, el camino más fácil es de nuevo el circuito
+
<center><math>0=2\pi\varepsilon_0 R(4V_2-V_0)</math>{{tose}}<math>V_2=\frac{V_0}{4}</math></center>
-
equivalente. Ya conocidos las cargas y potenciales, la energía se
+
-
calcula como
+
-
\[
+
-
\Ene=\frac{1}{2}Q_1V_1+\frac{Q_2}{V_2}+\frac{1}{2}Q_3V_3=
+
-
\frac{1}{2}Q_2V_2=\frac{3\pi\varepsilon_0 R}{4}V_0^2
+
-
\]
+
-
Obsérvese que los conductores $1$ y $3$ no contribuyen por anularse su
+
-
carga o su potencial.
+
-
Esta energía puede también calcularse a partir de la suma de energías
+
<center><math>Q_1=2\pi\varepsilon_0 R\left(V_0-\frac{V_0}{4}\right)=\frac{3\pi\varepsilon_0 R }{2}V_0</math>{{qquad}}<math>Q_3=2\pi\varepsilon_0 R\left(0-\frac{V_0}{4}\right)=-\frac{\pi\varepsilon_0 R }{2}V_0</math></center>
-
almacenadas en diferentes condensadores
+
 
-
\[
+
y ya están determinadas todas las incógnitas del problema.
-
\Ene=\frac{1}{2}\overline{C}_{11}V_1^2+\frac{1}{2}\overline{C}_{12}(V_1-V_2)^2+
+
-
\frac{1}{2}\overline{C}_{13}(V_1-V_3)^2%=\]\[
+
-
=\frac{4\pi\varepsilon_0
+
-
R}{2}\left(\frac{V_0}{4}\right)^2+\frac{2\pi\varepsilon_0
+
-
R}{2}\left(\frac{V_0}{4}-V_0\right)^2+
+
-
\frac{2\pi\varepsilon_0
+
-
R}{2}\left(\frac{V_0}{4}-0\right)^2=
+
-
\]\[
+
-
=\frac{1}{8}\pi\varepsilon_0 R V_0^2+\frac{9}{16}\pi\varepsilon_0 R
+
-
V_0^2+\frac{1}{16}\pi\varepsilon_0 R V_0^2=\frac{3}{4}\pi\varepsilon_0
+
-
RV_0^2
+
-
\]
+
[[Categoría:Problemas de campo eléctrico en presencia de conductores]]
[[Categoría:Problemas de campo eléctrico en presencia de conductores]]

Revisión de 20:11 3 dic 2008

Contenido

1 Enunciado

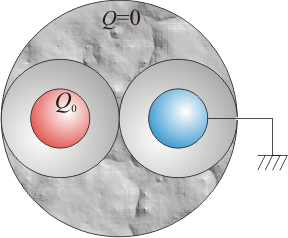
En una esfera metálica de radio R se han hecho dos cavidades, también esféricas, de radio R / 2. Concéntricas con cada una de estos huecos se hallan sendas esferas metálicas de radio R / 4. No hay más conductores en el sistema. Suponga que la esfera exterior se encuentra aislada y descargada; una de las esferas interiores almacena una carga Q0 y la otra se encuentra a tierra. ¿Cuál es la carga en cada conductor? ¿Y el potencial?

Halle la energía almacenada en el sistema.

2 Solución

2.1 Coeficientes de capacidad

El problema se reduce a la determinación de los coeficientes de capacidad del sistema. Conocidos éstos, con los datos del problema pueden determinarse las cargas y potenciales restantes.

La forma más sencilla de determinar la relación Q—V es a través del circuito equivalente. Tenemos tres conductores: la esfera exterior (que denominaremos “2”), la esfera a potencial V0 (“1”) y la que está a tierra (“3”).

En el circuito, cada conductor representa a un nodo. En principio, entre cada par de conductores se encuentra un condensador 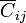\overline{C}_{ij}, más los que conectan a cada uno con el infinito, 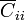\overline{C}_{ii}. Sin embargo, el conductor 2 apantalla al 1 y al 3, tanto entre sí como con el infinito (no puede haber líneas de campo que vayan del 1 al 3 o al exterior), por tanto,

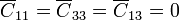
\overline{C}_{11}=\overline{C}_{33}=\overline{C}_{13}=0

A su vez, el conductor 1 forma con el conductor 2 un condensador esférico, de radio interior R / 4 y exterior R / 2. Lo mismo ocurre entre el 3 y el 2. Aplicando la fórmula para la capacidad de un condensador esférico 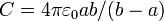C=4\pi\varepsilon_0 a b/(b-a), resulta

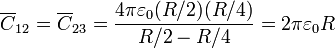
\overline{C}_{12}=\overline{C}_{23}=\frac{4\pi\varepsilon_0(R/2)(R/4)}{R/2-R/4}=2\pi\varepsilon_0 R

Podemos demostrar este resultado. Para calcular el coeficiente C21 debemos suponer el conductor 1 (una de las esferas interiores) a potencial unidad y el resto a tierra. En este caso, no hay campo eléctrico ni en el exterior del conductor 2, ni en el hueco entre el 2 y el 3, por estar todas las superficies a tierra.

En el hueco entre el conductor 1 y el 2 debemos resolver la ecuación de Laplace

\nabla^2\phi=0

con las condiciones de contorno

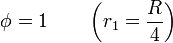
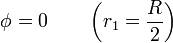
\phi=1\qquad \left(r_1=\frac{R}{4}\right)        \phi=0\qquad \left(r_1=\frac{R}{2}\right)

siendo r1 la distancia medida desde el centro de la esfera interior.

Al existir simetría de revolución dentro del hueco, la solución de la ecuación de Laplace es

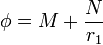
\phi = M + \frac{N}{r_1}

Imponiendo las condiciones de contorno

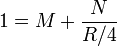
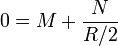
1=M+ \frac{N}{R/4}        0 = M + \frac{N}{R/2}

queda el potencial

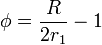
\phi=\frac{R}{2r_1}-1

La carga en la esfera interior, que por definición es el coeficiente C11 la hallamos a partir del flujo a través de una superficie que la envuelva.

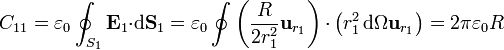
C_{11} = \varepsilon_0 \oint_{S_1}\mathbf{E}_1{\cdot}\mathrm{d}\mathbf{S}_1 = \varepsilon_0\oint\left(\frac{R}{2r_1^2}\mathbf{u}_{r_1}\right){\cdot}\left(r_1^2\,\mathrm{d}\Omega\mathbf{u}_{r_1}\right)= 2\pi\varepsilon_0 R

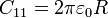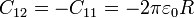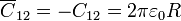siendo dΩ el diferencial de ángulo sólido. Esto nos da el coeficiente C_{11}=2\pi\varepsilon_0 R. Como este conductor 1 se encuentra en influencia total con el 2, C_{12}=-C_{11}=-2\pi\varepsilon_0 R. La capacidad equivalente entre los dos nodos será \overline{C}_{12}=-C_{12}=2\pi\varepsilon_0 R.

Por último queda por determinar la capacidad 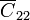\overline{C}_{22}. Ésta corresponde a las líneas que van del conductor 2 al infinito. El problema exterior es equivalente al de una sola esfera, cuya capacidad (calculable a partir de la de un condensador esférico haciendo 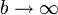b\to\infty) vale

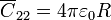
\overline{C}_{22}=4\pi\varepsilon_0 R

Con esto queda completada la relación entre cargas y capacidades. En general

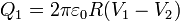
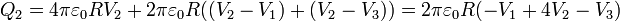
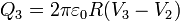
Q_1=2\pi\varepsilon_0 R(V_1-V_2)    Q_2=4\pi\varepsilon_0 RV_2+2\pi\varepsilon_0 R((V_2-V_1)+(V_2-V_3))=2\pi\varepsilon_0 R(-V_1+4V_2-V_3)        Q_3=2\pi\varepsilon_0 R(V_3-V_2)

En forma matricial

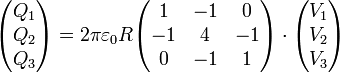
\begin{pmatrix}Q_1 \\ Q_2 \\ Q_3\end{pmatrix} = 2\pi\varepsilon_0R\begin{pmatrix}1 & -1 & 0 \\ -1 & 4 & -1 \\ 0 & -1 & 1\end{pmatrix}\cdot\begin{pmatrix}V_1 \\ V_2 \\ V_3\end{pmatrix}

2.2 Cargas y voltajes

En nuestro problema, los datos son

V1 = V0        Q2 = 0        V3 = 0
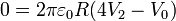
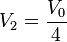
0=2\pi\varepsilon_0 R(4V_2-V_0)   \Rightarrow   V_2=\frac{V_0}{4}
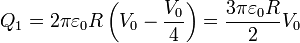
Q_1=2\pi\varepsilon_0 R\left(V_0-\frac{V_0}{4}\right)=\frac{3\pi\varepsilon_0 R }{2}V_0    Q_3=2\pi\varepsilon_0 R\left(0-\frac{V_0}{4}\right)=-\frac{\pi\varepsilon_0 R }{2}V_0

y ya están determinadas todas las incógnitas del problema.

Obtenido de "http://tesla.us.es/wiki/index.php/Esfera_conductora_con_dos_huecos_esf%C3%A9ricos"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace