Entrar Página Discusión Historial Go to the site toolbox

Calor necesario para evaporar hielo

De Laplace

(Diferencias entre revisiones)
(→Aumento de entropía)
 
(14 ediciones intermedias no se muestran.)
Línea 1: Línea 1:
 +
__TOC__
==Enunciado==
==Enunciado==
Calcule la cantidad de calor necesaria para llevar un bloque de hielo de 500 g inicialmente a −10 °C hasta el estado de vapor de agua a 115 °C, manteniéndose la presión constante en 101.3 kPa.
Calcule la cantidad de calor necesaria para llevar un bloque de hielo de 500 g inicialmente a −10 °C hasta el estado de vapor de agua a 115 °C, manteniéndose la presión constante en 101.3 kPa.
-
==Introducción==
+
 
 +
Halle el aumento de entropía en cada paso y el total del proceso.
 +
 
 +
==Calor necesario==
El proceso completo se compone de cinco partes: tres aumentos de temperatura y dos cambios de fase. Cada aumento de temperatura sigue la fórmula
El proceso completo se compone de cinco partes: tres aumentos de temperatura y dos cambios de fase. Cada aumento de temperatura sigue la fórmula
Línea 8: Línea 12:
donde <math>c</math> es el calor específico (a presión constante), que se supone con un valor constante para todo el rango de temperaturas (aunque diferente en cada fase). Un cálculo muy preciso debería tener en cuenta la variación del calor específico con la temperatura, resultando el calor
donde <math>c</math> es el calor específico (a presión constante), que se supone con un valor constante para todo el rango de temperaturas (aunque diferente en cada fase). Un cálculo muy preciso debería tener en cuenta la variación del calor específico con la temperatura, resultando el calor
-
<center><math>Q = \int_{T_i}^{T_f} mc\,\mathrm{d}T</math></center>
+
<center><math>Q = \int_{T_1}^{T_2} mc\,\mathrm{d}T</math></center>
Aquí nos quedaremos en la aproximación de que son constantes, con los valores respectivos para el hielo, el agua y el vapor
Aquí nos quedaremos en la aproximación de que son constantes, con los valores respectivos para el hielo, el agua y el vapor
Línea 18: Línea 22:
<center><math>Q = m\,\Delta h</math></center>
<center><math>Q = m\,\Delta h</math></center>
-
donde la entalpía específica de fusión y la de ebullición tienen los valores
+
donde la entalpía específica de fusión y la de vaporización tienen los valores
<center><math>\Delta h_f = 334\,\frac{\mathrm{kJ}}{\mathrm{kg}}\qquad\qquad \Delta h_v = 2257\,\frac{\mathrm{kJ}}{\mathrm{kg}}</math></center>
<center><math>\Delta h_f = 334\,\frac{\mathrm{kJ}}{\mathrm{kg}}\qquad\qquad \Delta h_v = 2257\,\frac{\mathrm{kJ}}{\mathrm{kg}}</math></center>
 +
 +
y las temperaturas de los puntos de fusión y de ebullición
 +
 +
<center><math>T_f = 273\,\mathrm{K}\qquad\qquad T_b = 373\,\mathrm{K}</math></center>
Aplicando estas fórmulas, obtenemos los siguientes valores:
Aplicando estas fórmulas, obtenemos los siguientes valores:
Línea 26: Línea 34:
;Hielo hasta el punto de fusión: Se trata de un aumento de temperatura de 10&deg;C, hasta los 0&deg;C
;Hielo hasta el punto de fusión: Se trata de un aumento de temperatura de 10&deg;C, hasta los 0&deg;C
-
<center><math>Q_1 = mc_h(T_1-T_0) = 0.500\cdot 2.11\cdot 10\,\mathrm{kJ} = 10.55\,\mathrm{kJ}</math></center>
+
<center><math>Q_1 = mc_h(T_f-T_1) = 0.500\times 2.11\times 10\,\mathrm{kJ} = 10.55\,\mathrm{kJ}</math></center>
;Fusión del hielo
;Fusión del hielo
-
<center><math>Q_2 = m\,\Delta h_f = 0.500\cdot 334\,\mathrm{kJ} = 167\,\mathrm{kJ}</math></center>
+
<center><math>Q_2 = m\,\Delta h_f = 0.500\times 334\,\mathrm{kJ} = 167\,\mathrm{kJ}</math></center>
;Calentamiento del agua hasta el punto de ebullición: es una subida de la temperatura en 100&deg;C
;Calentamiento del agua hasta el punto de ebullición: es una subida de la temperatura en 100&deg;C
-
<center><math>Q_3 = mc_a(T_2-T_1)=0.550\cdot 4.18\cdot 100\,\mathrm{kJ} = 209\,\mathrm{kJ}</math></center>
+
<center><math>Q_3 = mc_a(T_b-T_f)=0.550\times 4.18\times 100\,\mathrm{kJ} = 209\,\mathrm{kJ}</math></center>
;Ebullición del agua
;Ebullición del agua
-
<center><math>Q_4 = m\,\Delta h_v = 0.500\cdot 2257\,\mathrm{kJ} = 1128.5\,\mathrm{kJ}</math></center>
+
<center><math>Q_4 = m\,\Delta h_v = 0.500\times 2257\,\mathrm{kJ} = 1128.5\,\mathrm{kJ}</math></center>
;Calentamiento del vapor hasta la temperatura final: El vapor debe calentarse 15&deg;C hasta el estado final
;Calentamiento del vapor hasta la temperatura final: El vapor debe calentarse 15&deg;C hasta el estado final
-
<center><math>Q_5 = mc_{va}(T_3-T_2) = 0.500\cdot 2.09\cdot 15\,\mathrm{kJ} = 15.7\,\mathrm{kJ}</math></center>
+
<center><math>Q_5 = mc_{va}(T_2-T_b) = 0.500\times 2.09\times 15\,\mathrm{kJ} = 15.7\,\mathrm{kJ}</math></center>
Sumando todos los valores obtenemos el siguiente calor total
Sumando todos los valores obtenemos el siguiente calor total
Línea 50: Línea 58:
! Paso
! Paso
! <math>Q</math> (kJ)
! <math>Q</math> (kJ)
-
! Fracción del calor total (%)
+
! Fracción del calor total
|-
|-
| Hielo a 0&deg;C
| Hielo a 0&deg;C
| 10.6
| 10.6
-
| 0.7
+
| 0.7 %
|-
|-
| Fusión
| Fusión
| 167
| 167
-
| 10.9%
+
| 10.9 %
|-
|-
| Agua a 100&deg;C
| Agua a 100&deg;C
| 209
| 209
-
| 13.7%
+
| 13.7 %
|-
|-
| Ebullición
| Ebullición
| 1128.5
| 1128.5
-
| 73.7%
+
| 73.7 %
|-
|-
| Vapor a 115&deg;C
| Vapor a 115&deg;C
| 15.7
| 15.7
-
| 1.0%
+
| 1.0 %
|-
|-
! Total
! Total
Línea 79: Línea 87:
Vemos que, con diferencia, el proceso que requiere más calor es la conversión del agua en vapor de agua.
Vemos que, con diferencia, el proceso que requiere más calor es la conversión del agua en vapor de agua.
 +
==Aumento de entropía==
 +
Como en el cálculo del calor, para la entropía tenemos también cinco pasos.
 +
 +
En cada cambio de fase, por tratarse de un proceso isotermo
 +
 +
<center><math>\Delta S = \frac{m\,\Delta h}{T}</math></center>
 +
 +
En cada calentamiento a presión constante, suponiendo que la capacidad calorífica es independiente de la temperatura
 +
 +
<center><math>\Delta S = \int_{T_1}^{T_2}\frac{\delta Q}{T} = \int_{T_1}^{T_2}\frac{m\,c_p\,\mathrm{d}T}{T}=mc_p\ln\left(\frac{T_2}{T_1}\right)</math></center>
 +
 +
Esto nos da los siguientes valores:
 +
 +
;Hielo hasta el punto de fusión: Pasamos de 263&thinsp;K a 273&thinsp;K
 +
 +
<center><math>\Delta S_1 = mc_h\ln\left(\frac{T_f}{T_0}\right) = 0.500\times 2.11\times\ln\left(\frac{273}{263}\right)\,\frac{\mathrm{kJ}}{\mathrm{K}} = +39.4\,\frac{\mathrm{J}}{\mathrm{K}}</math></center>
 +
 +
;Fusión del hielo
 +
 +
<center><math>\Delta S_2 = \frac{m\,\Delta h_f}{T_f} = \frac{0.500\times 334}{273}\,\frac{\mathrm{kJ}}{\mathrm{K}} = +611.7\,\frac{\mathrm{J}}{\mathrm{K}}</math></center>
 +
 +
;Calentamiento del agua hasta el punto de ebullición: la temperatura pasa de 273&thinsp;K a 373&thinsp;K
 +
 +
<center><math>\Delta S_3 = mc_a\ln\left(\frac{T_b}{T_f}\right)=0.550\times 4.18\times\ln\left(\frac{373}{273}\right)\,\frac{\mathrm{kJ}}{\mathrm{K}} = +652.3\,\frac{\mathrm{J}}{\mathrm{K}}</math></center>
 +
 +
;Ebullición del agua
 +
 +
<center><math>\Delta S_4 = \frac{m\,\Delta h_v}{T_b} = \frac{0.500\times 2257}{373}\,\frac{\mathrm{kJ}}{\mathrm{K}} = +3025.5\,\frac{\mathrm{J}}{\mathrm{K}}</math></center>
 +
 +
;Calentamiento del vapor hasta la temperatura final:
 +
 +
<center><math>\Delta S_5 = mc_{va}\ln\left(\frac{T_2}{T_b}\right) = 0.500\times 2.09\times\ln\left(\frac{388}{273}\right) \,\frac{\mathrm{kJ}}{\mathrm{K}} = +41.0\,\frac{\mathrm{J}}{\mathrm{K}}</math></center>
 +
 +
Podemos incorporar estos resultados a la tabla anterior
 +
 +
{| class="bordeado"
 +
|-
 +
! Paso
 +
! <math>Q</math> (kJ)
 +
! Fracción del calor total
 +
! <math>\Delta S</math> (J/K)
 +
! Fracción de la producción de entropía
 +
|-
 +
| Hielo a 0&deg;C
 +
| 10.6
 +
| 0.7 %
 +
| 39.4
 +
| 0.9 %
 +
|-
 +
| Fusión
 +
| 167
 +
| 10.9 %
 +
| 611.7
 +
| 14.0 %
 +
|-
 +
| Agua a 100&deg;C
 +
| 209
 +
| 13.7 %
 +
| 652.3
 +
| 14.9 %
 +
|-
 +
| Ebullición
 +
| 1128.5
 +
| 73.7 %
 +
| 3025.5
 +
| 69.2 %
 +
|-
 +
| Vapor a 115&deg;C
 +
| 15.7
 +
| 1.0 %
 +
| 41.0
 +
| 0.9 %
 +
|-
 +
! Total
 +
! 1530.7
 +
! 100
 +
! 4369.9
 +
! 100
 +
|}
 +
 +
Vemos que la proporción mayor del aumento de entropía se debe al paso de líquido a vapor, aunque en proporción al aumento de entropía total constituye una fracción menor que el calor necesario respecto al calor total.
[[Categoría:Problemas del primer principio de la termodinámica (GIE)]]
[[Categoría:Problemas del primer principio de la termodinámica (GIE)]]
 +
[[Categoría:Problemas del segundo principio de la termodinámica (GIE)]]

última version al 10:00 18 mar 2014

Contenido

1 Enunciado

Calcule la cantidad de calor necesaria para llevar un bloque de hielo de 500 g inicialmente a −10 °C hasta el estado de vapor de agua a 115 °C, manteniéndose la presión constante en 101.3 kPa.

Halle el aumento de entropía en cada paso y el total del proceso.

2 Calor necesario

El proceso completo se compone de cinco partes: tres aumentos de temperatura y dos cambios de fase. Cada aumento de temperatura sigue la fórmula

Q = mc\,\Delta T

donde c es el calor específico (a presión constante), que se supone con un valor constante para todo el rango de temperaturas (aunque diferente en cada fase). Un cálculo muy preciso debería tener en cuenta la variación del calor específico con la temperatura, resultando el calor

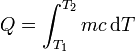
Q = \int_{T_1}^{T_2} mc\,\mathrm{d}T

Aquí nos quedaremos en la aproximación de que son constantes, con los valores respectivos para el hielo, el agua y el vapor

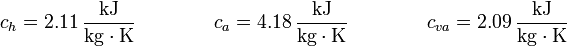
c_h = 2.11\,\frac{\mathrm{kJ}}{\mathrm{kg}\cdot\mathrm{K}}\qquad\qquad c_a = 4.18\,\frac{\mathrm{kJ}}{\mathrm{kg}\cdot\mathrm{K}}\qquad\qquad c_{va} = 2.09\,\frac{\mathrm{kJ}}{\mathrm{kg}\cdot\mathrm{K}}

En los cambios de fase la temperatura permanece constante y el calor se emplea en pasar el hielo a agua, o el agua a vapor. La cantidad de calor en cada caso es proporcional a la masa

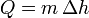
Q = m\,\Delta h

donde la entalpía específica de fusión y la de vaporización tienen los valores

\Delta h_f = 334\,\frac{\mathrm{kJ}}{\mathrm{kg}}\qquad\qquad \Delta h_v = 2257\,\frac{\mathrm{kJ}}{\mathrm{kg}}

y las temperaturas de los puntos de fusión y de ebullición

T_f = 273\,\mathrm{K}\qquad\qquad T_b = 373\,\mathrm{K}

Aplicando estas fórmulas, obtenemos los siguientes valores:

Hielo hasta el punto de fusión
Se trata de un aumento de temperatura de 10°C, hasta los 0°C
Q_1 = mc_h(T_f-T_1) = 0.500\times 2.11\times 10\,\mathrm{kJ} = 10.55\,\mathrm{kJ}
Fusión del hielo
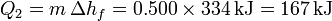
Q_2 = m\,\Delta h_f = 0.500\times 334\,\mathrm{kJ} = 167\,\mathrm{kJ}
Calentamiento del agua hasta el punto de ebullición
es una subida de la temperatura en 100°C
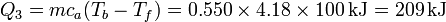
Q_3 = mc_a(T_b-T_f)=0.550\times 4.18\times 100\,\mathrm{kJ} = 209\,\mathrm{kJ}
Ebullición del agua
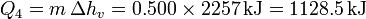
Q_4 = m\,\Delta h_v = 0.500\times 2257\,\mathrm{kJ} = 1128.5\,\mathrm{kJ}
Calentamiento del vapor hasta la temperatura final
El vapor debe calentarse 15°C hasta el estado final
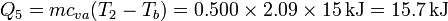
Q_5 = mc_{va}(T_2-T_b) = 0.500\times 2.09\times 15\,\mathrm{kJ} = 15.7\,\mathrm{kJ}

Sumando todos los valores obtenemos el siguiente calor total

Paso Q (kJ) Fracción del calor total
Hielo a 0°C 10.6 0.7 %
Fusión 167 10.9 %
Agua a 100°C 209 13.7 %
Ebullición 1128.5 73.7 %
Vapor a 115°C 15.7 1.0 %
Total 1530.7 100

Vemos que, con diferencia, el proceso que requiere más calor es la conversión del agua en vapor de agua.

3 Aumento de entropía

Como en el cálculo del calor, para la entropía tenemos también cinco pasos.

En cada cambio de fase, por tratarse de un proceso isotermo

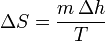
\Delta S = \frac{m\,\Delta h}{T}

En cada calentamiento a presión constante, suponiendo que la capacidad calorífica es independiente de la temperatura

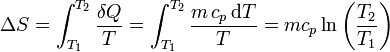
\Delta S = \int_{T_1}^{T_2}\frac{\delta Q}{T} = \int_{T_1}^{T_2}\frac{m\,c_p\,\mathrm{d}T}{T}=mc_p\ln\left(\frac{T_2}{T_1}\right)

Esto nos da los siguientes valores:

Hielo hasta el punto de fusión
Pasamos de 263 K a 273 K
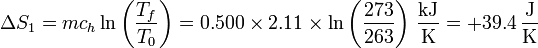
\Delta S_1 = mc_h\ln\left(\frac{T_f}{T_0}\right) = 0.500\times 2.11\times\ln\left(\frac{273}{263}\right)\,\frac{\mathrm{kJ}}{\mathrm{K}} = +39.4\,\frac{\mathrm{J}}{\mathrm{K}}
Fusión del hielo
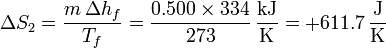
\Delta S_2 = \frac{m\,\Delta h_f}{T_f} = \frac{0.500\times 334}{273}\,\frac{\mathrm{kJ}}{\mathrm{K}} = +611.7\,\frac{\mathrm{J}}{\mathrm{K}}
Calentamiento del agua hasta el punto de ebullición
la temperatura pasa de 273 K a 373 K
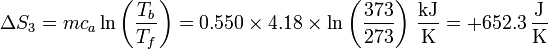
\Delta S_3 = mc_a\ln\left(\frac{T_b}{T_f}\right)=0.550\times 4.18\times\ln\left(\frac{373}{273}\right)\,\frac{\mathrm{kJ}}{\mathrm{K}} = +652.3\,\frac{\mathrm{J}}{\mathrm{K}}
Ebullición del agua
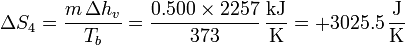
\Delta S_4 = \frac{m\,\Delta h_v}{T_b} = \frac{0.500\times 2257}{373}\,\frac{\mathrm{kJ}}{\mathrm{K}} = +3025.5\,\frac{\mathrm{J}}{\mathrm{K}}
Calentamiento del vapor hasta la temperatura final
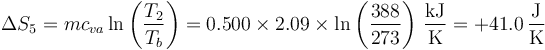
\Delta S_5 = mc_{va}\ln\left(\frac{T_2}{T_b}\right) = 0.500\times 2.09\times\ln\left(\frac{388}{273}\right) \,\frac{\mathrm{kJ}}{\mathrm{K}} = +41.0\,\frac{\mathrm{J}}{\mathrm{K}}

Podemos incorporar estos resultados a la tabla anterior

Paso Q (kJ) Fracción del calor total ΔS (J/K) Fracción de la producción de entropía
Hielo a 0°C 10.6 0.7 % 39.4 0.9 %
Fusión 167 10.9 % 611.7 14.0 %
Agua a 100°C 209 13.7 % 652.3 14.9 %
Ebullición 1128.5 73.7 % 3025.5 69.2 %
Vapor a 115°C 15.7 1.0 % 41.0 0.9 %
Total 1530.7 100 4369.9 100

Vemos que la proporción mayor del aumento de entropía se debe al paso de líquido a vapor, aunque en proporción al aumento de entropía total constituye una fracción menor que el calor necesario respecto al calor total.

Obtenido de "http://tesla.us.es/wiki/index.php/Calor_necesario_para_evaporar_hielo"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Esta página fue modificada por última vez el 10:00, 18 mar 2014. - Esta página ha sido visitada 45.320 veces. - Aviso legal - Acerca de Laplace