Segunda Prueba de Control 2013/14 (G.I.C.)
De Laplace
(Diferencias entre revisiones)
(→Péndulo con velocidad inicial) |
(→Barra girando) |
||
| (Una edición intermedia no se muestra.) | |||
| Línea 4: | Línea 4: | ||
#¿Cuál es la expresión de la velocidad en función del ángulo? | #¿Cuál es la expresión de la velocidad en función del ángulo? | ||
#Con los valores numéricos <math>L=10.0\,\mathrm{cm}</math>, <math>\theta_0=\pi/6</math>, ¿qué condición debe cumplir <math>v_0</math> para que la masa de una vuelta completa? | #Con los valores numéricos <math>L=10.0\,\mathrm{cm}</math>, <math>\theta_0=\pi/6</math>, ¿qué condición debe cumplir <math>v_0</math> para que la masa de una vuelta completa? | ||
| + | |||
| + | ==[[Disco apoyado en un escalón, Enero 2014 (G.I.C.)| Disco apoyado en un escalón]] == | ||
| + | [[Imagen:GIC_SPC_disco_escalon_enunciado.png|right]] | ||
| + | El disco de radio <math>R</math> y peso <math>P</math> de la figura sufre una fuerza horizontal | ||
| + | de módulo <math>F</math> aplicada en su punto más alto. El contacto en el punto <math>A</math> es | ||
| + | liso, mientras que el contacto en el punto <math>B</math> es rugoso con coeficiente de | ||
| + | rozamiento estático <math>\mu</math>. | ||
| + | |||
| + | #Calcula las fuerzas sobre el disco en situación de equilibrio estático. | ||
| + | #¿Qué condición debe cumplir el coeficiente de rozamiento para que pueda haber equilibrio estático? | ||
| + | # En este último caso, ¿qué condición debe valer la fuerza <math>F</math> para que el disco suba el escalón? | ||
==[[Barra girando, Enero 2014 (G.I.C.)| Barra girando]] == | ==[[Barra girando, Enero 2014 (G.I.C.)| Barra girando]] == | ||
| Línea 12: | Línea 23: | ||
#Si <math>I</math> es el momento de inercia de la barra respecto a un eje perpendicular al plano <math>OXY</math> y que pasa por el punto <math>O</math>, encuentra la ecuación diferencial que describe el movimiento de la barra. | #Si <math>I</math> es el momento de inercia de la barra respecto a un eje perpendicular al plano <math>OXY</math> y que pasa por el punto <math>O</math>, encuentra la ecuación diferencial que describe el movimiento de la barra. | ||
#Encuentra la expresión que da la velocidad angular con la que gira la barra en función del ángulo <math>\theta</math>. | #Encuentra la expresión que da la velocidad angular con la que gira la barra en función del ángulo <math>\theta</math>. | ||
| + | |||
| + | ==[[Características de una onda, Enero 2014 (G.I.C.) | Características de una onda]] == | ||
| + | [[Imagen:GIC_SPC_onda_viajera.png|right]] | ||
| + | La figura muestra una onda sinusoidal que viaja hacia la derecha en dos instantes de tiempo. La linea continua corresponde al instante <math>t=0.00\,\mathrm{s}</math> y la línea a trazos a <math>t=0.80\,\mathrm{s}</math>. Calcula | ||
| + | #La velocidad con la que se propaga la onda. | ||
| + | #La función matemática que describe la onda. | ||
| + | #La velocidad del punto <math>x=0</math> en el instante <math>t=0.80\,\mathrm{s}</math>. | ||
última version al 16:51 20 feb 2014
Contenido |
1 Péndulo con velocidad inicial
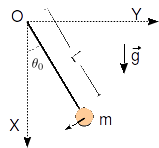
Una masa m cuelga de un hilo inextensible sin masa. En la posición inicial el hilo forma un ángulo θ0 con la vertical. La masa empieza a moverse con velocidad de módulo v0 y con la dirección y sentido indicados en la figura.
- ¿Cuál es la expresión de la velocidad en función del ángulo?
- Con los valores numéricos
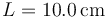, θ0 = π / 6, ¿qué condición debe cumplir v0 para que la masa de una vuelta completa?
2 Disco apoyado en un escalón
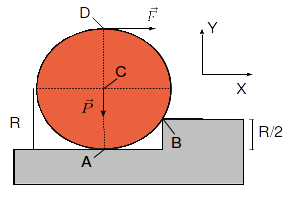
El disco de radio R y peso P de la figura sufre una fuerza horizontal de módulo F aplicada en su punto más alto. El contacto en el punto A es liso, mientras que el contacto en el punto B es rugoso con coeficiente de rozamiento estático μ.
- Calcula las fuerzas sobre el disco en situación de equilibrio estático.
- ¿Qué condición debe cumplir el coeficiente de rozamiento para que pueda haber equilibrio estático?
- En este último caso, ¿qué condición debe valer la fuerza F para que el disco suba el escalón?
3 Barra girando
La barra de la figura puede girar sobre su extremo inferior O. La barra es homogénea, de lonigtud L y masa M. En el instante inicial se encuentra en posición vertical (θ(0) = π / 2). En ese instante empieza a moverse de modo que el extremo A tiene una velocidad instantánea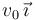 
.
- Calcula la velocidad angular de la barra en el instante inicial.
- Si I es el momento de inercia de la barra respecto a un eje perpendicular al plano OXY y que pasa por el punto O, encuentra la ecuación diferencial que describe el movimiento de la barra.
- Encuentra la expresión que da la velocidad angular con la que gira la barra en función del ángulo θ.
4 Características de una onda
La figura muestra una onda sinusoidal que viaja hacia la derecha en dos instantes de tiempo. La linea continua corresponde al instante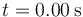 
y la línea a trazos a 
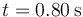. Calcula
- La velocidad con la que se propaga la onda.
- La función matemática que describe la onda.
- La velocidad del punto x = 0 en el instante .
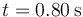