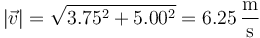Rotación tridimensional de una partícula
De Laplace
(Diferencias entre revisiones)
(Página creada con '==Enunciado== Una partícula describe un movimiento circular alrededor del origen de forma que en un cierto instante su posición la da el vector <center><math>\vec{r}=(16\vec{…') |
|||
| Línea 16: | Línea 16: | ||
==Velocidad y rapidez== | ==Velocidad y rapidez== | ||
| + | En lo que sigue, en todos los cálculos se usará el SI, por lo que escribiremos la posición como | ||
| + | |||
| + | <center><math>\vec{r}=(0.16\vec{\imath}+0.15\vec{\jmath} -0.12\vec{k})\,\mathrm{m}</math></center> | ||
| + | |||
| + | ===Velocidad lineal=== | ||
| + | Para una partícula que describe un movimiento de rotación alrededor del origen, su velocidad instantánea la da | ||
| + | |||
| + | <center><math>\vec{v}=\vec{\omega}\times\vec{r}=\left|\begin{matrix} \vec{\imath} & \vec{\jmath} & \vec{k} \\ -12 & 20 & 9 \\ 0.16 & 0.15 & -0.12\end{matrix}\right|=(-3.75\vec{\imath}+5.00\vec{k})\,\frac{\mathrm{m}}{\mathrm{s}}</math></center> | ||
| + | |||
| + | ===Rapidez=== | ||
| + | La rapidez o celeridad es igual al módulo de la velocidad | ||
| + | |||
| + | <center><math>\left|\vec{v}\right| = \sqrt{3.75^2+5.00^2}=6.25\,\frac{\mathrm{m}}{\mathrm{s}}</math></center> | ||
==Componentes intrínsecas de la aceleración== | ==Componentes intrínsecas de la aceleración== | ||
==Vectores tangente y normal== | ==Vectores tangente y normal== | ||
==Radio y centro de curvatura== | ==Radio y centro de curvatura== | ||
[[Categoría:Problemas de cinemática tridimensional de la partícula (GIE)]] | [[Categoría:Problemas de cinemática tridimensional de la partícula (GIE)]] | ||
Revisión de 00:12 13 ene 2014
Contenido |
1 Enunciado
Una partícula describe un movimiento circular alrededor del origen de forma que en un cierto instante su posición la da el vector
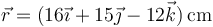
La velocidad angular de la partícula en el mismo instante es
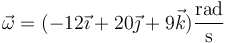
En el mismo instante la aceleración angular tiene sentido opuesto a la velocidad angular y módulo 0.50 rad/s². Para este instante, calcule:
- La velocidad lineal y la rapidez de la partícula.
- La aceleración tangencial y la aceleración normal, tanto escalares como vectores.
- Los vectores tangente y normal.
- El radio de curvatura y el centro de curvatura.
2 Velocidad y rapidez
En lo que sigue, en todos los cálculos se usará el SI, por lo que escribiremos la posición como
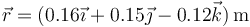
2.1 Velocidad lineal
Para una partícula que describe un movimiento de rotación alrededor del origen, su velocidad instantánea la da
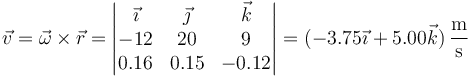
2.2 Rapidez
La rapidez o celeridad es igual al módulo de la velocidad