Potencial eléctrico de un segmento cargado
De Laplace
(Diferencias entre revisiones)
(Nueva página: ==Enunciado== Sea un segmento rectilíneo de longitud <math>L</math>, sobre el cual existe una densidad de carga uniforme <math>\lambda</math>. # Halle el potencial que produce en un...) |
(→Solución) |
||
| Línea 6: | Línea 6: | ||
==Solución== | ==Solución== | ||
| + | ===Potencial eléctrico=== | ||
| + | El cálculo del potencial eléctrico debido a un segmento es algo más complicado que el del [[Campo eléctrico de un segmento cargado|campo eléctrico]], pese a que la integral es aparentemente más simple. Para hallar el potencial por integración directa, debemos resolver la integral | ||
| + | |||
| + | <center><math>\phi(\mathbf{r})=\frac{1}{4\pi\varepsilon_0}\int \frac{\lambda(\mathbf{r'})}{|\mathbf{r}-\mathbf{r}'|}\mathrm{d}l'</math></center> | ||
| + | |||
| + | En nuestro caso, empleando los mismos ejes y las mismas variables que para el [[Campo eléctrico de un segmento cargado|cálculo del campo eléctrico]], nos queda | ||
| + | |||
| + | <center><math>\phi(\mathbf{r})=\frac{1}{4\pi\varepsilon_0}\int_{-L/2}^{L/2} \frac{\lambda}{\sqrt{x^2+y^2+(z-z')^2}}\mathrm{d}z'</math></center> | ||
| + | |||
| + | Empleando de nuevo el cambio de variable | ||
| + | |||
| + | ===Superficies equipotenciales=== | ||
[[Categoría:Problemas de electrostática en el vacío]] | [[Categoría:Problemas de electrostática en el vacío]] | ||
Revisión de 17:37 30 nov 2008
Contenido |
1 Enunciado
Sea un segmento rectilíneo de longitud L, sobre el cual existe una densidad de carga uniforme λ.
- Halle el potencial que produce en un punto cualquiera del espacio.
- Demuestre que las equipotenciales son elipsoides con focos los extremos del segmento.
2 Solución
2.1 Potencial eléctrico
El cálculo del potencial eléctrico debido a un segmento es algo más complicado que el del campo eléctrico, pese a que la integral es aparentemente más simple. Para hallar el potencial por integración directa, debemos resolver la integral
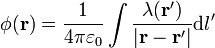
En nuestro caso, empleando los mismos ejes y las mismas variables que para el cálculo del campo eléctrico, nos queda
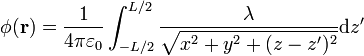
Empleando de nuevo el cambio de variable





