|
|
| (21 ediciones intermedias no se muestran.) |
| Línea 2: |
Línea 2: |
| | Un cable formado por dos hilos paralelos produce un campo eléctrico similar al producido por dos líneas infinitas con densidad de carga <math>\lambda</math> y <math>-\lambda</math>, situadas a una distancia <math>D</math> una de la otra. | | Un cable formado por dos hilos paralelos produce un campo eléctrico similar al producido por dos líneas infinitas con densidad de carga <math>\lambda</math> y <math>-\lambda</math>, situadas a una distancia <math>D</math> una de la otra. |
| | | | |
| - | Se trata de hallar la fuerza por unidad de longitud con que se atraen los dos hilos. Para ello, calcule:
| + | Halle la fuerza que uno de los hilos produce sobre un segmento de longitud <math>h</math> del otro hilo. |
| - | | + | |
| - | # El campo eléctrico en cualquier punto del espacio, creado por un segmento rectilíneo de longitud <math>L</math>, sobre el cual existe una densidad de carga uniforme <math>\lambda</math>.
| + | |
| - | # A partir del resultado anterior, halle el campo en cualquier punto debido a una línea de carga uniforme infinitamente larga.
| + | |
| - | # Halle la fuerza que uno de los hilos produce sobre un segmento de longitud <math>h</math> del otro hilo.
| + | |
| | | | |
| | ==Solución== | | ==Solución== |
| - | ===Campo de un segmento cargado===
| + | [[Imagen:doshiloscargados.png|left]] Para hallar la fuerza que uno de los hilos produce sobre otro situado paralelamente a él, a una distancia <math>D</math>, situamos los ejes de forma que el hilo que crea el campo (el de densidad de carga <math>+\lambda</math>) coincide con el eje <math>Z</math>, mientras que el segundo (con densidad <math>-\lambda</math>) pasa por el punto <math>x=D</math>, <math>y = 0</math>. |
| - | Sin pérdida de generalidad, podemos colocar el eje <math>z</math> sobre el segmento y el origen de coordenadas en su punto medio.
| + | |
| - | | + | |
| - | La expresión integral para el campo eléctrico debido a una distribución de carga lineal se expresa
| + | |
| - | | + | |
| - | <center><math>\mathbf{E}(\mathbf{r})=\frac{1}{4\pi\varepsilon_0} \int\lambda(\mathbf{r}')\frac{(\mathbf{r}-\mathbf{r}')}{|\mathbf{r}-\mathbf{r}'|^3}\,\mathrm{d}l'</math></center>
| + | |
| - | | + | |
| - | En nuestro caso, la posición de las fuentes es
| + | |
| - | | + | |
| - | <center><math>x'=0\quad y'=0\quad z'=z'</math>{{qquad}}<math>z'\in\left[-\frac{L}{2},\frac{L}{2}\right]</math></center>
| + | |
| - | | + | |
| - | | + | |
| - | <center><math>\mathrm{d}\mathbf{r}'=\mathrm{d}z'\,\mathbf{u}_{z}</math>{{qquad}}{{qquad}}<math>\mathrm{d}l'=|\mathrm{d}\mathbf{r}'|=\mathrm{d}z'</math></center>
| + | |
| - | | + | |
| - | por lo que la integral se convierte en
| + | |
| - | | + | |
| - | <center><math>\mathbf{E}(\mathbf{r})=\frac{1}{4\pi\varepsilon_0} \int_{-L/2}^{L/2}
| + | |
| - | \!\!\lambda \frac{(x\mathbf{u}_{x}+y\mathbf{u}_{y}+(z-z')\mathbf{u}_{z})}
| + | |
| - | {\left(x^2+y^2+(z-z')^2\right)^{3/2}}\,\mathrm{d}z'</math></center>
| + | |
| - | | + | |
| - | Separando componente a componente
| + | |
| - | | + | |
| - | <center><math>E_x=
| + | |
| - | \frac{1}{4\pi\varepsilon_0} \int_{-L/2}^{L/2}\!\!\lambda \frac{ x}
| + | |
| - | {\left(x^2+y^2+(z-z')^2\right)^{3/2}}\,\mathrm{d}z'</math></center>
| + | |
| - | | + | |
| - | <center><math>E_y=
| + | |
| - | \frac{1}{4\pi\varepsilon_0} \int_{-L/2}^{L/2}\!\!\lambda \frac{y}
| + | |
| - | {\left(x^2+y^2+(z-z')^2\right)^{3/2}}\,\mathrm{d}z'
| + | |
| - | </math></center> | + | |
| - | | + | |
| - | <center><math>E_z= \frac{1}{4\pi\varepsilon_0} \int_{-L/2}^{L/2}\!\!\lambda \frac{
| + | |
| - | (z-z')}
| + | |
| - | {\left(x^2+y^2+(z-z')^2\right)^{3/2}}\,\mathrm{d}z'
| + | |
| - | </math></center>
| + | |
| - | | + | |
| - | Podemos llevar a cabo estas integrales mediante el cambio de variable
| + | |
| - | | + | |
| - | <center><math>z'-z=\sqrt{x^2+y^2}\tan\alpha</math>{{qquad}}{{qquad}}
| + | |
| - | <math>\mathrm{d}z'=\frac{\sqrt{x^2+y^2}}{\cos^2\alpha}\,\mathrm{d}\alpha</math></center>
| + | |
| - | | + | |
| - | Este ángulo posee interpretación geométrica ya que es el que forma la dirección al punto donde está la fuente con la horizontal.
| + | |
| - | | + | |
| - | Con este cambio las integrales quedan
| + | |
| - | | + | |
| - | <center><math>E_x=
| + | |
| - | \frac{1}{4\pi\varepsilon_0} \int_{\alpha_1}^{\alpha_2}\frac{\lambda x\cos\alpha}
| + | |
| - | {x^2+y^2}\,\mathrm{d}\alpha=\frac{1}{4\pi\varepsilon_0} \frac{\lambda
| + | |
| - | x}{x^2+y^2}(\mathrm{sen}\,\alpha_2-\mathrm{sen}\,\alpha_1)</math></center>
| + | |
| - | | + | |
| - | <center><math>E_y=
| + | |
| - | \frac{1}{4\pi\varepsilon_0} \int_{\alpha_1}^{\alpha_2}\frac{\lambda y\cos\alpha}
| + | |
| - | {x^2+y^2}\,\mathrm{d}\alpha=\frac{1}{4\pi\varepsilon_0} \frac{\lambda
| + | |
| - | y}{x^2+y^2}(\mathrm{sen}\,\alpha_2-\mathrm{sen}\,\alpha_1)</math></center>
| + | |
| - | | + | |
| - | | + | |
| - | <center><math>E_z= -\frac{1}{4\pi\varepsilon_0}
| + | |
| - | \int_{\alpha_1}^{\alpha_2}\frac{\lambda
| + | |
| - | \mathrm{sen}\,\alpha}
| + | |
| - | {\sqrt{x^2+y^2}}\,\mathrm{d}\alpha=
| + | |
| - | \frac{1}{4\pi\varepsilon_0} \frac{\lambda
| + | |
| - | }{\sqrt{x^2+y^2}}(\cos\alpha_2-\cos\alpha_1)
| + | |
| - | </math></center> | + | |
| - | | + | |
| - | Los senos y cosenos que aparecen en las expresiones anteriores corresponden a los valores límite de <math>\alpha</math> y su relación con las coordenadas cartesianas es
| + | |
| - | | + | |
| - | <math>\mathrm{sen}\,\alpha_2=\frac{L/2-z}{\sqrt{x^2+y^2+(z-L/2)^2}}</math>{{qquad}}<math>\cos\alpha_2=\frac{\sqrt{x^2+y^2}}{\sqrt{x^2+y^2+(z-L/2)^2}}</math>
| + | |
| - | | + | |
| - | <center><math>\mathrm{sen}\,\alpha_1=-\frac{L/2+z}{\sqrt{x^2+y^2+(z+L/2)^2}}</math>{{qquad}}<math>\cos\alpha_1=\frac{\sqrt{x^2+y^2}}{\sqrt{x^2+y^2+(z+L/2)^2}}</math></center>
| + | |
| - | | + | |
| - | Agrupando los resultados tenemos la forma vectorial
| + | |
| | | | |
| - | <center><math>\mathbf{E}=\frac{\lambda}{4\pi\eps}\left(\frac{x\mathbf{u}_{x}+y\mathbf{u}_{y}}{x^2+y^2}
| + | Aplicando la expresión para el [[Campo_eléctrico_de_un_segmento_cargado#Campo_de_un_hilo_infinito|campo creado por un hilo infinito]], el campo debido al primer hilo es |
| - | \left(\mathrm{sen}\,\alpha_2-\mathrm{sen}\,\alpha_1\right)+
| + | |
| - | \frac{\mathbf{u}_{z}(\cos\alpha_2-\cos\alpha_1)}{\sqrt{x^2+y^2}}\right)
| + | |
| - | </math></center>
| + | |
| | | | |
| - | Si expresamos el campo en coordenadas cilíndricas centradas en el hilo nos queda
| + | <center><math>\mathbf{E}_1(x,y) = \frac{\lambda}{2\pi \varepsilon_0}\,\frac{x\mathbf{u}_x+y\mathbf{u}_y}{x^2+y^2}</math></center> |
| | | | |
| - | <center><math>\mathbf{E}=\frac{\lambda}{4\pi\eps\rho}
| + | y su valor en cada uno de los puntos del segundo hilo es |
| - | \left(\left(\mathrm{sen}\,\alpha_2-\mathrm{sen}\,\alpha_1\right)\mathbf{u}_{\rho}+
| + | |
| - | \left(\cos\alpha_2-\cos\alpha_1\right)\mathbf{u}_{z}\right)
| + | |
| - | </math></center>
| + | |
| | | | |
| - | que podemos leer como el campo posee una componente en la dirección radial perpendicular al eje del segmento y una componente paralela a
| + | <center><math>\mathbf{E}_1(x=D,y=0) = \frac{\lambda}{2\pi \varepsilon_0}\,\frac{D\mathbf{u}_x+0\mathbf{u}_y}{D^2+0^2} = \frac{\lambda}{2\pi\varepsilon_0D}\mathbf{u}_x</math></center> |
| - | él. Esta interpretación nos seguirá valiendo cuando el eje <math>z</math> no esté situado sobre el segmento.
| + | |
| | | | |
| - | Para ello consideraremos un segmento <math>AB</math> y un punto de observación arbitrario <math>P</math>. Trazamos la recta perpendicular a <math>AB</math> por <math>P</math>. Esta recta cortará a la primera en un punto <math>C</math>. La variable <math>\rho</math> será la longitud del segmento <math>PC</math>. El ángulo <math>\alpha_1</math> será el que forma esta perpendicular con el segmento <math>PA</math> y el <math>\alpha_2</math> con el segmento <math>PB</math>. Ambos ángulos serán positivos si la perpendicular queda por detrás del segmento (considerando '''adelante''' aquél en que apunta <math>\mathbf{u}_z</math>) y negativos en caso contrario. Si la perpendicular incide sobre el segmento <math>AB</math>, el ángulo <math>\alpha_2</math> será positivo y el <math>\alpha_1</math> negativo.
| + | La fuerza sobre un elemento de carga del segundo hilo es |
| | | | |
| - | Un límite interesante de la expresión anterior es aquel en que <math>L\to\infty</math>, entonces, cualquiera que sea el punto de observación, <math>\alpha_1\to -\pi/2</math>, <math>\alpha_2\to \pi/2</math>, por lo que
| + | <center><math>\mathrm{d}\mathbf{F}_{21}=\mathrm{d}q_2\mathbf{E}_1 = -(\lambda\,\mathrm{d}z) \left(\frac{\lambda}{2\pi\varepsilon_0D}\mathbf{u}_x\right) = -\frac{\lambda^2\mathbf{u}_x}{2\pi\varepsilon_0D}\mathrm{d}z</math></center> |
| | | | |
| - | <center><math>\mathbf{E}=\frac{\lambda}{4\pi\eps\rho}\left((1-(-1))\mathbf{u}_{\rho}+(0-0)\mathbf{u}_{z}\right)= | + | Esta fuerza diferencial es independiente de la altura <math>z</math> a la que se encuentre el elemento (lo cual es evidente dada la simetría traslacional del sistema. Por tanto, la fuerza sobre un segmento de longitud <math>h</math> del segundo hilo es |
| - | \frac{\lambda}{2\pi\eps\rho}\mathbf{u}_{\rho}</math></center>
| + | |
| | | | |
| - | Este resultado se obtiene, empleando la ley de Gauss, en otro problema.
| + | <center><math>\mathbf{F}_21 = \int_0^h \mathrm{d}\mathbf{F}_{21} = -\frac{\lambda^2h\mathbf{u}_x}{2\pi\varepsilon_0D}</math></center> |
| | | | |
| - | ===Campo de un hilo infinito===
| + | Esta fuerza va en el sentido de <math>-\mathbf{u}_x</math>, siendo <math>\mathbf{u}_x</math> el vector que va del primer hilo perpendicularmente al segundo. Esto quiere decir que la fuerza es atractiva, como corresponde a dos hilos cargados con signos opuestos. |
| - | ===Fuerza entre los hilos===
| + | |
| | | | |
| - | [[Categoría:Problemas de electrostática]] | + | [[Categoría:Problemas de electrostática en el vacío]] |
Un cable formado por dos hilos paralelos produce un campo eléctrico similar al producido por dos líneas infinitas con densidad de carga λ y − λ, situadas a una distancia D una de la otra.
Para hallar la fuerza que uno de los hilos produce sobre otro situado paralelamente a él, a una distancia
, situamos los ejes de forma que el hilo que crea el campo (el de densidad de carga
.
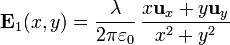
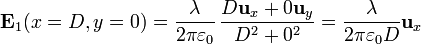
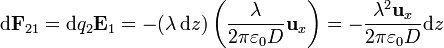

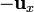 , siendo
, siendo 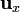 el vector que va del primer hilo perpendicularmente al segundo. Esto quiere decir que la fuerza es atractiva, como corresponde a dos hilos cargados con signos opuestos.
el vector que va del primer hilo perpendicularmente al segundo. Esto quiere decir que la fuerza es atractiva, como corresponde a dos hilos cargados con signos opuestos.






