Fuerza entre dos hilos cargados
De Laplace
(→Solución) |
(→Solución) |
||
| Línea 5: | Línea 5: | ||
==Solución== | ==Solución== | ||
| - | [[Imagen:doshiloscargados.png|left]]Para hallar la fuerza que uno de los hilos produce sobre otro situado paralelamente a él, a una distancia <math>D</math>, situamos los ejes de forma que el hilo que crea el campo (el de densidad de carga <math>+\lambda</math>) coincide con el eje <math>Z</math>, mientras que el segundo (con densidad <math>-\lambda</math>) pasa por el punto <math>x=D</math>, <math>y = 0</math>. | + | [[Imagen:doshiloscargados.png|left]] Para hallar la fuerza que uno de los hilos produce sobre otro situado paralelamente a él, a una distancia <math>D</math>, situamos los ejes de forma que el hilo que crea el campo (el de densidad de carga <math>+\lambda</math>) coincide con el eje <math>Z</math>, mientras que el segundo (con densidad <math>-\lambda</math>) pasa por el punto <math>x=D</math>, <math>y = 0</math>. |
| + | |||
| + | Aplicando la expresión para el [[Campo_y_potencial_debidos_a_un_segmento_cargado#Campo_de_un_hilo_infinito|campo creado por un hilo infinito]] el campo debido al primer hilo es | ||
| + | |||
| + | <center><math>\mathbf{E}_1(x,y) = \frac{\lambda}{2\pi \varepsilon_0}\,\frac{x\mathbf{u}_x+y\mathbf{u}_y}{x^2+y^2}</math></center> | ||
| + | |||
| + | y su valor en cada uno de los puntos del segundo hilo es | ||
<center><math>\mathbf{E}_1(x=D,y=0) = \frac{\lambda}{2\pi \varepsilon_0}\,\frac{D\mathbf{u}_x+0\mathbf{u}_y}{D^2+0^2} = \frac{\lambda}{2\pi\varepsilon_0D}\mathbf{u}_x</math></center> | <center><math>\mathbf{E}_1(x=D,y=0) = \frac{\lambda}{2\pi \varepsilon_0}\,\frac{D\mathbf{u}_x+0\mathbf{u}_y}{D^2+0^2} = \frac{\lambda}{2\pi\varepsilon_0D}\mathbf{u}_x</math></center> | ||
Revisión de 11:51 30 nov 2008
1 Enunciado
Un cable formado por dos hilos paralelos produce un campo eléctrico similar al producido por dos líneas infinitas con densidad de carga λ y − λ, situadas a una distancia D una de la otra.
Halle la fuerza que uno de los hilos produce sobre un segmento de longitud h del otro hilo.
2 Solución
Aplicando la expresión para el campo creado por un hilo infinito el campo debido al primer hilo es
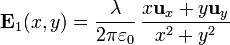
y su valor en cada uno de los puntos del segundo hilo es
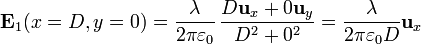
La fuerza sobre un elemento de carga del segundo hilo es
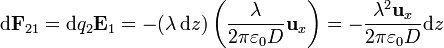
Esta fuerza diferencial es independiente de la altura z a la que se encuentre el elemento (lo cual es evidente dada la simetría traslacional del sistema. Por tanto, la fuerza sobre un segmento de longitud h del segundo hilo es
Esta fuerza va en el sentido de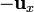 
, siendo 
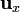el vector que va del primer hilo perpendicularmente al segundo. Esto quiere decir que la fuerza es atractiva, como corresponde a dos hilos cargados con signos opuestos.
