Entrar Página Discusión Historial Go to the site toolbox

Parámetro arco de una hélice (G.I.A.)

De Laplace

(Diferencias entre revisiones)
(→Enunciado)
(→Triedro intrínseco)
 
(2 ediciones intermedias no se muestran.)
Línea 8: Línea 8:
     x(\lambda) = a \cos\lambda\\
     x(\lambda) = a \cos\lambda\\
     y(\lambda) = a \,\mathrm{sen}\,\lambda\\
     y(\lambda) = a \,\mathrm{sen}\,\lambda\\
-
     z(\lambda) = a \lambda
+
     z(\lambda) = h \lambda
   \end{array}
   \end{array}
\right.
\right.
Línea 20: Línea 20:
== Solución ==
== Solución ==
-
El diferencial del parámetro natural es el módulo del desplazamiento
+
=== Distancia recorrida ===
-
elemental
+
Podemos calcular la distancia recorrida sobre la hélice sumando los módulos de los <math>\mathrm{d}\vec{r} </math> obtenidos al variar el parámetro una cantidad infinitesimal <math>\mathrm{d}\lambda </math>. La expresión de <math>\mathrm{d}\vec{r} </math> es
-
<center><math>
+
<center>
-
  \mathrm{d}s=|\mathrm{d}\vec{r}| =\mathrm{d}\lambda\,
+
<math>
-
  \sqrt{\left(\dfrac{\mathrm{d}x}{\mathrm{d}\lambda}\right)^2+
+
\mathrm{d}\vec{r} = \left(\dfrac{\mathrm{d}\vec{r}}{\mathrm{d}\lambda}\right)\,\mathrm{d}\lambda
-
    \left(\dfrac{\mathrm{d}y}{\mathrm{d}\lambda}\right)^2+
+
</math>
-
    \left(\dfrac{\mathrm{d}z}{\mathrm{d}\lambda}\right)^2}
+
</center>
-
</math></center>
+
Derivando el vector tenemos
-
Derivando en la ecuación paramétrica de la curva obtenemos
+
<center>
-
<center><math>
+
<math>
-
  \mathrm{d}s=\mathrm{d}\lambda\,\sqrt{a^2+h^2}
+
\left(\dfrac{\mathrm{d}\vec{r}}{\mathrm{d}\lambda}\right) =
-
</math></center>
+
-a\cos\lambda\,\vec{\imath}
-
Integrando en ambos lados obtenemos
+
+
-
<center><math>
+
+a\,\mathrm{sen}\,\lambda\,\vec{\jmath}
-
  s = \lambda\,\sqrt{a^2+h^2} + A
+
+
-
</math></center>
+
h\,\vec{k}
-
donde <math>A</math> es una constante. Podemos fijar su valor imponiendo <math>s=0</math>
+
</math>
-
cuando <math>\lambda=0</math>. Esto es simplemente cambiar el punto inicial de la
+
</center>
-
curva. Así pues el parámetro arco es
+
La distancia recorrida en este paso infinitesimal es
-
<center><math>
+
<center>
-
  s = \lambda\,\sqrt{a^2+h^2}
+
<math>
-
</math></center>
+
\mathrm{d}s=|\mathrm{d}\vec{r}|=\left|\dfrac{\mathrm{d}\vec{r}}{\mathrm{d}\lambda}\right| \,\mathrm{d}\lambda =
-
Reparametrizamos la ecuación vectorial de la curva
+
\mathrm{d}\lambda\,\sqrt{a^2\cos^2\lambda + a^2\mathrm{sen}^2\lambda + h^2}
-
<center><math>
+
=
-
  \Gamma\,:\,\vec{r} = \vec{r}(s)
+
\mathrm{d}\lambda\,\sqrt{a^2+h^2}
-
  \left\{
+
</math>
-
    \begin{array}{l}
+
</center>
-
      x(s) = a \cos\left(\dfrac{s}{\sqrt{a^2+h^2}} \right)\\ \\
+
Si empezamos a contar la distancia recorrida en <math>\lambda=0 </math> la distancia para un valor de <math>\lambda </math> es
-
      y(s) = a \,\mathrm{sen}\,\left(\dfrac{s}{\sqrt{a^2+h^2}} \right)\\ \\
+
<center>
-
      z(s) = \dfrac{hs}{\sqrt{a^2+h^2}}
+
<math>
-
    \end{array}
+
\int\limits_{0}^{s(\lambda)}\mathrm{d}s =
-
  \right.
+
\int\limits_{0}^{s(\lambda)}|\mathrm{d}\vec{r}| =
-
</math></center>
+
\int\limits_0^{\lambda}\sqrt{a^2+h^2}\,\mathrm{d}\lambda
-
Ahora podemos calcular el triedro intrínseco de forma sencilla.  
+
</math>
 +
</center>
 +
Integrando obtenemos
 +
<center>
 +
<math>
 +
s(\lambda) = \lambda\,\sqrt{a^2+h^2}
 +
</math>
 +
</center>
 +
 
 +
La distancia recorrida sobre la curva recibe el nombre de parámetro arco. Puede utilizarse también para parametrizar la curva.
 +
 
 +
===Triedro intrínseco ===
 +
 
 +
Calculamos el triedro intrínseco en cada punto de la curva usando las expresiones que dependen sólo de la parametrización de la curva, no de las variables cinemáticas ( velocidad y aceleración ).
El vector tangente es
El vector tangente es
-
<center><math>
+
<center>
-
  \vec{T} = \vec{r}\,' =
+
<math>
-
  \left[
+
\overrightarrow{T}(\lambda) = \dfrac{\displaystyle\dfrac{\mathrm{d}\vec{r}}{\mathrm{d}\lambda}}{\displaystyle\left|\dfrac{\mathrm{d}\vec{r}}{\mathrm{d}\lambda}\right|}
-
    -\dfrac{a}{\sqrt{a^2+h^2}}\,\mathrm{sen}\,\left(\dfrac{s}{\sqrt{a^2+h^2}}
+
=
-
    \right),
+
-\dfrac{a\,\mathrm{sen}\,\lambda}{\sqrt{a^2+h^2}}\,\vec{\imath}
-
    \dfrac{a}{\sqrt{a^2+h^2}}\cos\left(\dfrac{s}{\sqrt{a^2+h^2}}
+
+
-
    \right),
+
\dfrac{a\cos\lambda}{\sqrt{a^2+h^2}}\,\vec{\jmath}
-
    \dfrac{h}{\sqrt{a^2+h^2}}
+
+
-
  \right]
+
\dfrac{h}{\sqrt{a^2+h^2}}\,\vec{k}
-
</math></center>
+
</math>
-
Podemos comprobar que <math>|\vec{r}\,'|=1</math>, dado que <math>\vec{r}</math> está
+
</center>
-
expresado en el parámetro arco.
+
-
El vector normal es
+
El vector normal se define en términos de la derivada del vector tangente respecto al parámetro.
-
<center><math>
+
<center>
-
  \vec{N} = \dfrac{\vec{T}'}{|\vec{T}'|} =
+
<math>
-
  \left[
+
\overrightarrow{N}(\lambda) = \dfrac{\displaystyle\dfrac{\mathrm{d}\overrightarrow{T}}{\mathrm{d}\lambda}}{\displaystyle\left|\dfrac{\mathrm{d}\overrightarrow{T}}{\mathrm{d}\lambda}\right|}
-
    -\cos\left(\dfrac{s}{\sqrt{a^2+h^2}}\right),
+
</math>
-
    -\,\mathrm{sen}\,\left(\dfrac{s}{\sqrt{a^2+h^2}}\right),
+
</center>
-
    0
+
Derivando el vector tangente
-
  \right]
+
<center>
-
</math></center>
+
<math>
-
Y el vector binormal es
+
\dfrac{\mathrm{d}\overrightarrow{T}}{\mathrm{d}\lambda}=
-
<center><math>
+
-\dfrac{a\cos\lambda}{\sqrt{a^2+h^2}}\,\vec{\imath}
-
  \vec{B} = \vec{T}\times\vec{N} =  
+
-
-
  \left[
+
\dfrac{a\,\mathrm{sen}\,\lambda}{\sqrt{a^2+h^2}}\,\vec{\jmath}
-
    \dfrac{h}{\sqrt{a^2+h^2}}\,\mathrm{sen}\,\left(\dfrac{s}{\sqrt{a^2+h^2}}
+
\dfrac{a}{\sqrt{a^2+h^2}}
-
    \right),
+
=
-
    -\dfrac{h}{\sqrt{a^2+h^2}}\cos\left(\dfrac{s}{\sqrt{a^2+h^2}}
+
\dfrac{a}{\sqrt{a^2+h^2}}
-
    \right),
+
\left(-\cos\lambda\,\vec{\imath} - \mathrm{sen}\,\lambda\,\vec{\jmath}\right)
-
    \dfrac{a}{\sqrt{a^2+h^2}}
+
</math>
-
  \right]
+
</center>
-
</math></center>
+
El módulo de este vector es
 +
<center>
 +
<math>
 +
\left|\dfrac{\mathrm{d}\overrightarrow{T}}{\mathrm{d}\lambda}\right|
 +
=\dfrac{a}{\sqrt{a^2+h^2}}
 +
</math>
 +
</center>
 +
Y el vector normal es
 +
<center>
 +
<math>
 +
\overrightarrow{N}(\lambda) = -\cos\lambda\,\vec{\imath} - \mathrm{sen}\,\lambda\,\vec{\jmath}
 +
</math>
 +
</center>
 +
El vector binormal se define como
 +
<center>
 +
<math>
 +
\overrightarrow{B}(\lambda) = \overrightarrow{T}\times\overrightarrow{N}
 +
=
 +
\dfrac{h\,\mathrm{sen}\,\lambda}{\sqrt{a^2+h^2}}\,\vec{\imath}-
 +
\dfrac{h\,\mathrm{cos}\,\lambda}{\sqrt{a^2+h^2}}\,\vec{\jmath}
 +
+\dfrac{a}{\sqrt{a^2+h^2}}\,\vec{k}
 +
</math>
 +
</center>
 +
 
 +
=== Curvatura===
 +
La curvatura es el módulo de la derivada del vector tangente, cuando este está expresado en términos del parámetro arco. Sin embargo, no tenemos el vector <math>\overrightarrow{T} </math> en términos del parámetro arco, sino del parámetro <math>\lambda </math>. Tenemos que usar la regla de la cadena para encontrar la derivada en función del parámetro natural.Esto es
 +
<center>
 +
<math>
 +
\kappa =
 +
\left|
 +
\dfrac{\mathrm{d}\overrightarrow{T}}{\mathrm{d}s}
 +
\right|
 +
=
 +
\left|
 +
\dfrac{\mathrm{d}\overrightarrow{T}}{\mathrm{d}\lambda}
 +
\right|
 +
\,\left|\dfrac{\mathrm{d}\lambda}{\mathrm{d}s}
 +
\right|
 +
</math>
 +
</center>
 +
A partir de la última fórmula del primer apartado, podemos despejar <math>\lambda </math> a partir del parámetro arco
 +
<center>
 +
<math>
 +
\lambda = \dfrac{s}{\sqrt{a^2+h^2}}
 +
</math>
 +
</center>
 +
Y derivamos aquí
 +
<center>
 +
<math>
 +
\dfrac{\mathrm{d}\lambda}{\mathrm{d}s}=
 +
\dfrac{1}{\sqrt{a^2+h^2}}
 +
</math>
 +
</center>
 +
Con lo cual la curvatura es
 +
<center>
 +
<math>
 +
\kappa =
 +
\left|
 +
\dfrac{\mathrm{d}\overrightarrow{T}}{\mathrm{d}s}
 +
\right|
 +
=
 +
\left|
 +
\dfrac{\mathrm{d}\overrightarrow{T}}{\mathrm{d}\lambda}
 +
\right|
 +
\,\left|\dfrac{\mathrm{d}\lambda}{\mathrm{d}s}
 +
\right|
 +
=
 +
\dfrac{a}{\sqrt{a^2+h^2}}\,
 +
\dfrac{1}{\sqrt{a^2+h^2}}
 +
=
 +
\dfrac{a}{a^2+h^2}
 +
</math>
 +
</center>
 +
 
 +
El radio de curvatura es
 +
<center>
 +
<math>
 +
R_{\kappa} = \dfrac{1}{\kappa} = \dfrac{{a^2+h^2}}{a}
 +
</math>
 +
</center>
-
Por definición, el radio de curvatura es
 
-
<center><math>
 
-
  R_{\kappa}=\dfrac{1}{\kappa}=\dfrac{1}{|\vec{T}'|} =
 
-
  \dfrac{a^2+h^2}{a}
 
-
</math></center>
 
-
Es interesante observar que si <math>h=0</math> reobtenemos el radio de curvatura
 
-
de una circunferencia.
 
[[Categoría:Cinemática del punto material|1]]
[[Categoría:Cinemática del punto material|1]]
[[Categoría:Física I (G.I.A.)]]
[[Categoría:Física I (G.I.A.)]]
[[Categoría:Física I (G.I.T.I.)]]
[[Categoría:Física I (G.I.T.I.)]]
 +
[[Categoría:Física I (G.I.C.)]]

última version al 09:49 16 oct 2013

Contenido

1 Enunciado

Sea la hélice Γ descrita en un sistema de referencia cartesiano OXYZ por las siguientes ecuaciones paramétricas:

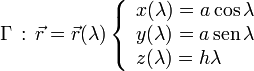
\Gamma\,:\,\vec{r} = \vec{r}(\lambda) \left\{ \begin{array}{l} x(\lambda) = a \cos\lambda\\ y(\lambda) = a \,\mathrm{sen}\,\lambda\\ z(\lambda) = h \lambda \end{array} \right.

donde a y h son constantes conocidas.

  1. Determina la longitud recorrida sobre la hélice (parámetro arco) en función del parámetro λ.
  2. Obtén los vectores del triedro intrínseco en cada punto de dicha curva.
  3. Calcula su radio de curvatura.

2 Solución

2.1 Distancia recorrida

Podemos calcular la distancia recorrida sobre la hélice sumando los módulos de los 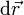\mathrm{d}\vec{r} obtenidos al variar el parámetro una cantidad infinitesimal dλ. La expresión de 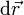\mathrm{d}\vec{r} es

\mathrm{d}\vec{r} = \left(\dfrac{\mathrm{d}\vec{r}}{\mathrm{d}\lambda}\right)\,\mathrm{d}\lambda

Derivando el vector tenemos

\left(\dfrac{\mathrm{d}\vec{r}}{\mathrm{d}\lambda}\right) = -a\cos\lambda\,\vec{\imath} + +a\,\mathrm{sen}\,\lambda\,\vec{\jmath} + h\,\vec{k}

La distancia recorrida en este paso infinitesimal es

\mathrm{d}s=|\mathrm{d}\vec{r}|=\left|\dfrac{\mathrm{d}\vec{r}}{\mathrm{d}\lambda}\right| \,\mathrm{d}\lambda = \mathrm{d}\lambda\,\sqrt{a^2\cos^2\lambda + a^2\mathrm{sen}^2\lambda + h^2} = \mathrm{d}\lambda\,\sqrt{a^2+h^2}

Si empezamos a contar la distancia recorrida en λ = 0 la distancia para un valor de λ es

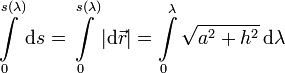
\int\limits_{0}^{s(\lambda)}\mathrm{d}s = \int\limits_{0}^{s(\lambda)}|\mathrm{d}\vec{r}| = \int\limits_0^{\lambda}\sqrt{a^2+h^2}\,\mathrm{d}\lambda

Integrando obtenemos

s(\lambda) = \lambda\,\sqrt{a^2+h^2}

La distancia recorrida sobre la curva recibe el nombre de parámetro arco. Puede utilizarse también para parametrizar la curva.

2.2 Triedro intrínseco

Calculamos el triedro intrínseco en cada punto de la curva usando las expresiones que dependen sólo de la parametrización de la curva, no de las variables cinemáticas ( velocidad y aceleración ).

El vector tangente es

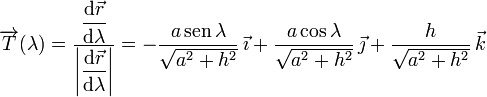
\overrightarrow{T}(\lambda) = \dfrac{\displaystyle\dfrac{\mathrm{d}\vec{r}}{\mathrm{d}\lambda}}{\displaystyle\left|\dfrac{\mathrm{d}\vec{r}}{\mathrm{d}\lambda}\right|} = -\dfrac{a\,\mathrm{sen}\,\lambda}{\sqrt{a^2+h^2}}\,\vec{\imath} + \dfrac{a\cos\lambda}{\sqrt{a^2+h^2}}\,\vec{\jmath} + \dfrac{h}{\sqrt{a^2+h^2}}\,\vec{k}

El vector normal se define en términos de la derivada del vector tangente respecto al parámetro.

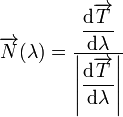
\overrightarrow{N}(\lambda) = \dfrac{\displaystyle\dfrac{\mathrm{d}\overrightarrow{T}}{\mathrm{d}\lambda}}{\displaystyle\left|\dfrac{\mathrm{d}\overrightarrow{T}}{\mathrm{d}\lambda}\right|}

Derivando el vector tangente

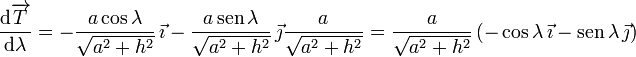
\dfrac{\mathrm{d}\overrightarrow{T}}{\mathrm{d}\lambda}= -\dfrac{a\cos\lambda}{\sqrt{a^2+h^2}}\,\vec{\imath} - \dfrac{a\,\mathrm{sen}\,\lambda}{\sqrt{a^2+h^2}}\,\vec{\jmath} \dfrac{a}{\sqrt{a^2+h^2}} = \dfrac{a}{\sqrt{a^2+h^2}} \left(-\cos\lambda\,\vec{\imath} - \mathrm{sen}\,\lambda\,\vec{\jmath}\right)

El módulo de este vector es

\left|\dfrac{\mathrm{d}\overrightarrow{T}}{\mathrm{d}\lambda}\right| =\dfrac{a}{\sqrt{a^2+h^2}}

Y el vector normal es

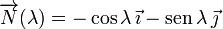
\overrightarrow{N}(\lambda) = -\cos\lambda\,\vec{\imath} - \mathrm{sen}\,\lambda\,\vec{\jmath}

El vector binormal se define como

\overrightarrow{B}(\lambda) = \overrightarrow{T}\times\overrightarrow{N} = \dfrac{h\,\mathrm{sen}\,\lambda}{\sqrt{a^2+h^2}}\,\vec{\imath}- \dfrac{h\,\mathrm{cos}\,\lambda}{\sqrt{a^2+h^2}}\,\vec{\jmath} +\dfrac{a}{\sqrt{a^2+h^2}}\,\vec{k}

2.3 Curvatura

La curvatura es el módulo de la derivada del vector tangente, cuando este está expresado en términos del parámetro arco. Sin embargo, no tenemos el vector 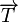\overrightarrow{T} en términos del parámetro arco, sino del parámetro λ. Tenemos que usar la regla de la cadena para encontrar la derivada en función del parámetro natural.Esto es

\kappa = \left| \dfrac{\mathrm{d}\overrightarrow{T}}{\mathrm{d}s} \right| = \left| \dfrac{\mathrm{d}\overrightarrow{T}}{\mathrm{d}\lambda} \right| \,\left|\dfrac{\mathrm{d}\lambda}{\mathrm{d}s} \right|

A partir de la última fórmula del primer apartado, podemos despejar λ a partir del parámetro arco

\lambda = \dfrac{s}{\sqrt{a^2+h^2}}

Y derivamos aquí

\dfrac{\mathrm{d}\lambda}{\mathrm{d}s}= \dfrac{1}{\sqrt{a^2+h^2}}

Con lo cual la curvatura es

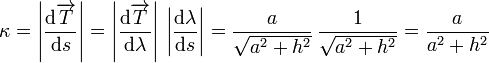
\kappa = \left| \dfrac{\mathrm{d}\overrightarrow{T}}{\mathrm{d}s} \right| = \left| \dfrac{\mathrm{d}\overrightarrow{T}}{\mathrm{d}\lambda} \right| \,\left|\dfrac{\mathrm{d}\lambda}{\mathrm{d}s} \right| = \dfrac{a}{\sqrt{a^2+h^2}}\, \dfrac{1}{\sqrt{a^2+h^2}} = \dfrac{a}{a^2+h^2}

El radio de curvatura es

R_{\kappa} = \dfrac{1}{\kappa} = \dfrac{{a^2+h^2}}{a}

Obtenido de "http://tesla.us.es/wiki/index.php/Par%C3%A1metro_arco_de_una_h%C3%A9lice_(G.I.A.)"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Esta página fue modificada por última vez el 09:49, 16 oct 2013. - Esta página ha sido visitada 10.059 veces. - Aviso legal - Acerca de Laplace