6.6. Disco en manivela ranurada

De Laplace

(Diferencias entre revisiones)

última version al 12:25 24 sep 2013

Contenido

1 Enunciado
2 Posición del CIR
3 Reducción cinemática
- 3.1 Directamente
- 3.2 Por composición de movimientos
  - 3.2.1 Velocidad
  - 3.2.2 Velocidad angular
4 Tipo de movimiento

1 Enunciado

El sistema de la figura está constituido por un plano vertical fijo $O X 1 Y 1$ (sólido “1”) que en todo instante contiene a otros dos sólidos en movimiento: un disco de radio $R$ y centro $C$ (sólido “2”), que rueda sin deslizar sobre el eje horizontal $O X 1$ ; y una manivela ranurada $O A$ (sólido “0”), que es obligada a girar con velocidad angular constante $Ω$ alrededor de un eje permanente de rotación que pasa por el punto $O$ y es perpendicular al plano fijo definido como sólido “1” (eje $O Z 1$ ). Los movimientos de ambos sólidos se hallan vinculados entre sí porque el centro C del disco está obligado a deslizar en todo instante a lo largo de la ranura de la manivela.

Considerando el movimiento {20} como el movimiento problema, se pide:

Haciendo uso de procedimientos gráficos, determinar la posición del CIR de dicho movimiento {20}.
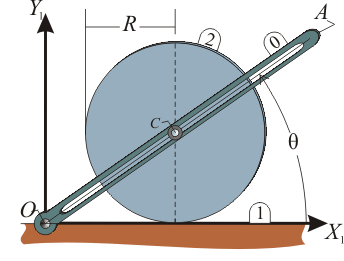
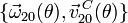Utilizando como parámetro geométrico el ángulo $θ$ indicado en la figura, obtener la reducción cinemática del movimiento {20} en el punto C, $\{\vec{\omega}_{20} (\theta), \vec{v}_{20}^{\, C} (\theta)\}$ .
Clasificar el movimiento {20} en el instante en que $θ = π / 2$ especificando si se trata de rotación, traslación, movimiento helicoidal o reposo.

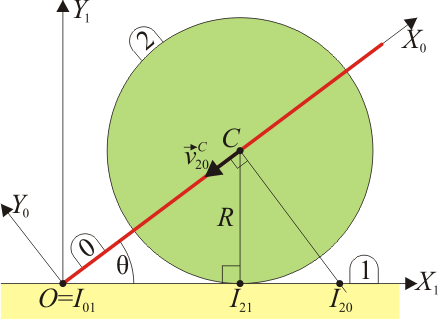
2 Posición del CIR

Por el teorema de los tres centros, el CIR $I 20$ debe estar alineado con el $I 21$ y el $I 01$ .

Por tratarse de una rodadura sin deslizamiento, el CIR del movimiento {21} es el punto de contacto de la rueda con el eje horizontal.

El CIR del movimiento {01} es el punto O, de articulación de la manivela con el eje.

Por estar alineado con estos dos, el CIR del movimiento {20} debe encontrarse sobre el eje horizontal $O X 1$ . Queda por determinar dónde exactamente.

El vínculo de que el centro C del disco se encuentre sobre la manivela obliga a que la velocidad del punto C en el movimiento {20} sea necesariamente a lo largo de ésta. Puesto que el CIR se encuentra sobre la recta que pasa por C y es perpendicular a la velocidad 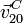$\vec{v}^C_{20}$ basta con trazar la perpendicular a la manivela en C. El punto donde esta recta corta al eje $O X 1$ es el CIR $I 20$ .

El vector de posición de este punto será de la forma

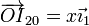
$\overrightarrow{OI}_{20}=x\vec{\imath}_1$

El valor de $x$ lo obtenemos aplicando trigonometría. El segmento $O I 20$ es la hipotenusa de un triángulo rectángulo cuyo cateto contiguo es $O C$ . Por tanto

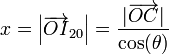
$x = \left|\overrightarrow{OI}_{20}\right| = \frac{|\overrightarrow{OC}|}{\cos(\theta)}$

A su vez OC es la hipotenusa de un triángulo rectángulo cuyo cateto opuesto mide R, el radio del disco

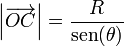
$\left|\overrightarrow{OC}\right| = \frac{R}{\mathrm{sen}(\theta)}$

Por tanto

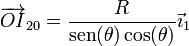
$\overrightarrow{OI}_{20}=\frac{R}{\mathrm{sen}(\theta)\cos(\theta)}\vec{\imath}_1$

3 Reducción cinemática

3.1 Directamente

3.1.1 Velocidad

La velocidad de C la podemos hallar derivando el vector de posición en un sistema de referencia “0” ligado a la manivela. Tomando como eje $O X 0$ el que va a lo largo de la manivela, el vector de posición relativo es

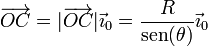
$\overrightarrow{OC}=|\overrightarrow{OC}|\vec{\imath}_0 = \frac{R}{\mathrm{sen}(\theta)}\vec{\imath}_0$

Derivando en esta expresión

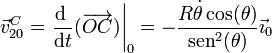
$\vec{v}^C_{20}=\left.\frac{\mathrm{d}\ }{\mathrm{d}t}(\overrightarrow{OC})\right|_0 = -\frac{R\dot{\theta}\cos(\theta)}{\mathrm{sen}^2(\theta)}\vec{\imath}_0$

3.1.2 Velocidad angular

Puesto que conocemos la posición del CIR $I 20$ podemos hallar la velocidad angular empleando la relación

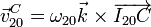
$\vec{v}^C_{20}=\omega_{20}\vec{k}\times\overrightarrow{I_{20}C}$

El vector de posición relativo desde el CIR va en la dirección del eje $O Y 0$ y tiene por módulo el cateto opuesto de un triángulo rectángulo

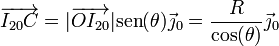
$\overrightarrow{I_{20}C}=|\overrightarrow{OI_{20}}|\mathrm{sen}(\theta)\vec{\jmath}_0 = \frac{R}{\cos(\theta)}\vec{\jmath}_0$

Por tanto,

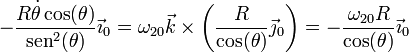
$-\frac{R\dot{\theta}\cos(\theta)}{\mathrm{sen}^2(\theta)}\vec{\imath}_0 = \omega_{20}\vec{k}\times\left(\frac{R}{\cos(\theta)}\vec{\jmath}_0\right)=-\frac{\omega_{20}R}{\cos(\theta)}\vec{\imath}_0$

Despejando

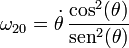
$\omega_{20}=\dot{\theta}\,\frac{\cos^2(\theta)}{\mathrm{sen}^2(\theta)}$

3.1.3 Expresión de la reducción cinemática

Reuniendo los dos resultados obtenemos la reducción cinemática

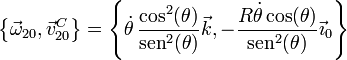
$\left\{\vec{\omega}_{20},\vec{v}^C_{20}\right\}=\left\{\dot{\theta}\,\frac{\cos^2(\theta)}{\mathrm{sen}^2(\theta)}\vec{k},-\frac{R\dot{\theta}\cos(\theta)}{\mathrm{sen}^2(\theta)}\vec{\imath}_0\right\}$

Empleando la base ligada al sólido “1”, esto queda

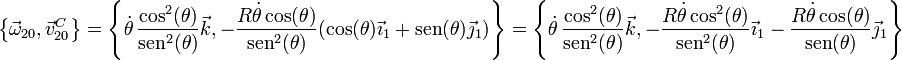
$\left\{\vec{\omega}_{20},\vec{v}^C_{20}\right\}=\left\{\dot{\theta}\,\frac{\cos^2(\theta)}{\mathrm{sen}^2(\theta)}\vec{k},-\frac{R\dot{\theta}\cos(\theta)}{\mathrm{sen}^2(\theta)}(\cos(\theta)\vec{\imath}_1+\mathrm{sen}(\theta)\vec{\jmath}_1)\right\}=\left\{\dot{\theta}\,\frac{\cos^2(\theta)}{\mathrm{sen}^2(\theta)}\vec{k},-\frac{R\dot{\theta}\cos^2(\theta)}{\mathrm{sen}^2(\theta)}\vec{\imath}_1-\frac{R\dot{\theta}\cos(\theta)}{\mathrm{sen}(\theta)}\vec{\jmath}_1\right\}$

3.2 Por composición de movimientos

3.2.1 Velocidad

Alternativamente, podemos obtener la velocidad de C empleando la fórmula de composición de velocidades

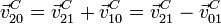
$\vec{v}^C_{20}=\vec{v}^C_{21}+\vec{v}^C_{10}=\vec{v}^C_{21}-\vec{v}^C_{01}$

La velocidad en el movimiento {01} corresponde a una rotación alrededor de O

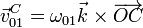
$\vec{v}^C_{01}=\omega_{01}\vec{k}\times\overrightarrow{OC}$

siendo su velocidad angular

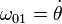
$\omega_{01}=\dot{\theta}$

y el vector de posición

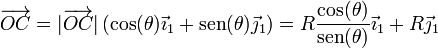
$\overrightarrow{OC}=|\overrightarrow{OC}|\left(\cos(\theta)\vec{\imath}_1+\mathrm{sen}(\theta)\vec{\jmath}_1\right) = R\frac{\cos(\theta)}{\mathrm{sen}(\theta)}\vec{\imath}_1+R\vec{\jmath}_1$

lo que nos da la velocidad

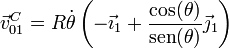
$\vec{v}^C_{01}=R\dot{\theta}\left(-\vec{\imath}_1+\frac{\cos(\theta)}{\mathrm{sen}(\theta)}\vec{\jmath}_1\right)$

La velocidad de C en el movimiento {21} la podemos hallar derivando la posición en el sistema “1”, que conocemos en todo momento

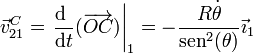
$\vec{v}^C_{21}=\left.\frac{\mathrm{d}\ }{\mathrm{d}t}(\overrightarrow{OC})\right|_1 = -\frac{R\dot{\theta}}{\mathrm{sen}^2(\theta)}\vec{\imath}_1$

Resulta una velocidad horizontal como corresponde a que el punto C se desplaza paralelamente al eje $O X 1$ .

Componiendo las dos velocidades

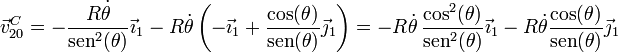
$\vec{v}^C_{20}= -\frac{R\dot{\theta}}{\mathrm{sen}^2(\theta)}\vec{\imath}_1 - R\dot{\theta}\left(-\vec{\imath}_1+\frac{\cos(\theta)}{\mathrm{sen}(\theta)}\vec{\jmath}_1\right) = -R\dot{\theta}\,\frac{\cos^2(\theta)}{\mathrm{sen}^2(\theta)}\vec{\imath}_1-R\dot{\theta}\frac{\cos(\theta)}{\mathrm{sen}(\theta)}\vec{\jmath}_1$

3.2.2 Velocidad angular

Igualmente, podemos hallar la velocidad angular del movimiento {20} como

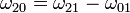
$\omega_{20}=\omega_{21}-\omega_{01}\,$

siendo

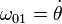
$\omega_{01}=\dot{\theta}$

La velocidad angular del movimiento {21} la podemos hallar a partir de la velocidad de C

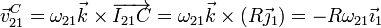
$\vec{v}^C_{21}=\omega_{21}\vec{k}\times\overrightarrow{I_{21}C}=\omega_{21}\vec{k}\times(R\vec{\jmath}_1)=-R\omega_{21}\vec{\imath}_1$

Igualando esta expresión a la velocidad lineal calculada anteriormente y despejando queda

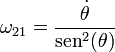
$\omega_{21}=\frac{\dot{\theta}}{\mathrm{sen}^2(\theta)}$

Llevando esto a la fórmula de composición de velocidades angulares, llegamos a

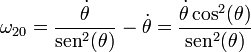
$\omega_{20}=\frac{\dot{\theta}}{\mathrm{sen}^2(\theta)}-\dot{\theta}=\frac{\dot{\theta}\cos^2(\theta)}{\mathrm{sen}^2(\theta)}$

Reuniendo la velocidad y la velocidad angular nos queda la misma reducción cinemática que ya expresamos anteriormente.

4 Tipo de movimiento

Cuando $θ = π / 2$ , la reducción cinemática se reduce a

$\left\{\vec{\omega}_{20},\vec{v}^C_{20}\right\}=\left.\left\{\dot{\theta}\,\frac{\cos^2(\theta)}{\mathrm{sen}^2(\theta)}\vec{k},-\frac{R\dot{\theta}\cos(\theta)}{\mathrm{sen}^2(\theta)}(\cos(\theta)\vec{\imath}_1+\mathrm{sen}(\theta)\vec{\jmath}_1)\right\}\right|_{\theta=\pi/2}=\{\vec{0},\vec{0}\}$

y por tanto el disco se encuentra instantáneamente en reposo respecto a la manivela.

@@ Línea 12: / Línea 12: @@
 ==Posición del CIR==
 Por el teorema de los tres centros, el CIR <math>I_{20}</math> debe estar alineado con el <math>I_{21}</math> y el <math>I_{01}</math>.
+[[Archivo:manivela-ranurada-01.png|right]]
 Por tratarse de una rodadura sin deslizamiento, el CIR del movimiento {21} es el punto de contacto de la rueda con el eje horizontal.
-El CIR del movimiento {20} es el punto O, de articulación de la manivela con el eje.
+El CIR del movimiento {01} es el punto O, de articulación de la manivela con el eje.
 Por estar alineado con estos dos, el CIR del movimiento {20} debe encontrarse  sobre el eje horizontal <math>OX_1</math>. Queda por determinar dónde exactamente.
@@ Línea 25: / Línea 27: @@
 <center><math>\overrightarrow{OI}_{20}=x\vec{\imath}_1</math></center>
-El valor de x lo obtenemos aplicando trigonometría. El segmento <math>OI_{20}</math> es la hipotenusa de un triángulo rectángulo cuyo cateto contiguo es <math>OC</math>. Por tanto
+El valor de <math>x</math> lo obtenemos aplicando trigonometría. El segmento <math>OI_{20}</math> es la hipotenusa de un triángulo rectángulo cuyo cateto contiguo es <math>OC</math>. Por tanto
 <center><math>x = \left|\overrightarrow{OI}_{20}\right| = \frac{|\overrightarrow{OC}|}{\cos(\theta)}</math></center>
@@ Línea 38: / Línea 40: @@
 ==Reducción cinemática==
+===Directamente===
+====Velocidad====
+La velocidad de C la podemos hallar derivando el vector de posición en un sistema de referencia &ldquo;0&rdquo; ligado a la manivela. Tomando como eje <math>OX_0</math> el que va a lo largo de la manivela, el vector de posición  relativo es
+<center><math>\overrightarrow{OC}=|\overrightarrow{OC}|\vec{\imath}_0 = \frac{R}{\mathrm{sen}(\theta)}\vec{\imath}_0</math></center>
+Derivando en esta expresión
+<center><math>\vec{v}^C_{20}=\left.\frac{\mathrm{d}\ }{\mathrm{d}t}(\overrightarrow{OC})\right|_0 = -\frac{R\dot{\theta}\cos(\theta)}{\mathrm{sen}^2(\theta)}\vec{\imath}_0</math></center>
+====Velocidad angular====
+Puesto que conocemos la posición del CIR <math>I_{20}</math> podemos hallar la velocidad angular empleando la relación
+<center><math>\vec{v}^C_{20}=\omega_{20}\vec{k}\times\overrightarrow{I_{20}C}</math></center>
+El vector de posición relativo desde el CIR va en la dirección del eje <math>OY_0</math> y tiene por módulo el cateto opuesto de un triángulo rectángulo
+<center><math>\overrightarrow{I_{20}C}=|\overrightarrow{OI_{20}}|\mathrm{sen}(\theta)\vec{\jmath}_0 = \frac{R}{\cos(\theta)}\vec{\jmath}_0</math></center>
+Por tanto,
+<center><math>-\frac{R\dot{\theta}\cos(\theta)}{\mathrm{sen}^2(\theta)}\vec{\imath}_0 = \omega_{20}\vec{k}\times\left(\frac{R}{\cos(\theta)}\vec{\jmath}_0\right)=-\frac{\omega_{20}R}{\cos(\theta)}\vec{\imath}_0</math></center>
+Despejando
+<center><math>\omega_{20}=\dot{\theta}\,\frac{\cos^2(\theta)}{\mathrm{sen}^2(\theta)}</math></center>
+====Expresión de la reducción cinemática====
+Reuniendo los dos resultados obtenemos la reducción cinemática
+<center><math>\left\{\vec{\omega}_{20},\vec{v}^C_{20}\right\}=\left\{\dot{\theta}\,\frac{\cos^2(\theta)}{\mathrm{sen}^2(\theta)}\vec{k},-\frac{R\dot{\theta}\cos(\theta)}{\mathrm{sen}^2(\theta)}\vec{\imath}_0\right\}</math></center>
+Empleando la base ligada al sólido &ldquo;1&rdquo;, esto queda
+<center><math>\left\{\vec{\omega}_{20},\vec{v}^C_{20}\right\}=\left\{\dot{\theta}\,\frac{\cos^2(\theta)}{\mathrm{sen}^2(\theta)}\vec{k},-\frac{R\dot{\theta}\cos(\theta)}{\mathrm{sen}^2(\theta)}(\cos(\theta)\vec{\imath}_1+\mathrm{sen}(\theta)\vec{\jmath}_1)\right\}=\left\{\dot{\theta}\,\frac{\cos^2(\theta)}{\mathrm{sen}^2(\theta)}\vec{k},-\frac{R\dot{\theta}\cos^2(\theta)}{\mathrm{sen}^2(\theta)}\vec{\imath}_1-\frac{R\dot{\theta}\cos(\theta)}{\mathrm{sen}(\theta)}\vec{\jmath}_1\right\}</math></center>
+===Por composición de movimientos===
+====Velocidad====
+Alternativamente, podemos obtener la velocidad de C empleando la fórmula de composición de velocidades
+<center><math>\vec{v}^C_{20}=\vec{v}^C_{21}+\vec{v}^C_{10}=\vec{v}^C_{21}-\vec{v}^C_{01}</math></center>
+La velocidad en el movimiento {01} corresponde a una rotación alrededor de O
+<center><math>\vec{v}^C_{01}=\omega_{01}\vec{k}\times\overrightarrow{OC}</math></center>
+siendo su velocidad angular
+<center><math>\omega_{01}=\dot{\theta}</math></center>
+y el vector de posición
+<center><math>\overrightarrow{OC}=|\overrightarrow{OC}|\left(\cos(\theta)\vec{\imath}_1+\mathrm{sen}(\theta)\vec{\jmath}_1\right) = R\frac{\cos(\theta)}{\mathrm{sen}(\theta)}\vec{\imath}_1+R\vec{\jmath}_1</math></center>
+lo que nos da la velocidad
+<center><math>\vec{v}^C_{01}=R\dot{\theta}\left(-\vec{\imath}_1+\frac{\cos(\theta)}{\mathrm{sen}(\theta)}\vec{\jmath}_1\right)</math></center>
+La velocidad de C en el movimiento {21} la podemos hallar derivando la posición en el sistema &ldquo;1&rdquo;, que conocemos en todo momento
+<center><math>\vec{v}^C_{21}=\left.\frac{\mathrm{d}\ }{\mathrm{d}t}(\overrightarrow{OC})\right|_1 = -\frac{R\dot{\theta}}{\mathrm{sen}^2(\theta)}\vec{\imath}_1</math></center>
+Resulta una velocidad horizontal como corresponde a que el punto C se desplaza paralelamente al eje <math>OX_1</math>.
+Componiendo las dos velocidades
+<center><math>\vec{v}^C_{20}= -\frac{R\dot{\theta}}{\mathrm{sen}^2(\theta)}\vec{\imath}_1 - R\dot{\theta}\left(-\vec{\imath}_1+\frac{\cos(\theta)}{\mathrm{sen}(\theta)}\vec{\jmath}_1\right) =
+-R\dot{\theta}\,\frac{\cos^2(\theta)}{\mathrm{sen}^2(\theta)}\vec{\imath}_1-R\dot{\theta}\frac{\cos(\theta)}{\mathrm{sen}(\theta)}\vec{\jmath}_1</math></center>
+====Velocidad angular====
+Igualmente, podemos hallar la velocidad angular del movimiento {20} como
+<center><math>\omega_{20}=\omega_{21}-\omega_{01}\,</math></center>
+siendo
+<center><math>\omega_{01}=\dot{\theta}</math></center>
+La velocidad angular del movimiento {21} la podemos hallar a partir de la velocidad de C
+<center><math>\vec{v}^C_{21}=\omega_{21}\vec{k}\times\overrightarrow{I_{21}C}=\omega_{21}\vec{k}\times(R\vec{\jmath}_1)=-R\omega_{21}\vec{\imath}_1</math></center>
+Igualando esta expresión a la velocidad lineal calculada anteriormente y despejando queda
+<center><math>\omega_{21}=\frac{\dot{\theta}}{\mathrm{sen}^2(\theta)}</math></center>
+Llevando esto a la fórmula de composición de velocidades angulares, llegamos a
+<center><math>\omega_{20}=\frac{\dot{\theta}}{\mathrm{sen}^2(\theta)}-\dot{\theta}=\frac{\dot{\theta}\cos^2(\theta)}{\mathrm{sen}^2(\theta)}</math></center>
+Reuniendo la velocidad y la velocidad angular nos queda la misma reducción cinemática que ya expresamos anteriormente.
 ==Tipo de movimiento==
+Cuando <math>\theta=\pi/2</math>, la reducción cinemática se reduce a
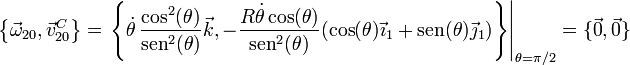
+<center><math>\left\{\vec{\omega}_{20},\vec{v}^C_{20}\right\}=\left.\left\{\dot{\theta}\,\frac{\cos^2(\theta)}{\mathrm{sen}^2(\theta)}\vec{k},-\frac{R\dot{\theta}\cos(\theta)}{\mathrm{sen}^2(\theta)}(\cos(\theta)\vec{\imath}_1+\mathrm{sen}(\theta)\vec{\jmath}_1)\right\}\right|_{\theta=\pi/2}=\{\vec{0},\vec{0}\}</math></center>
+y por tanto el disco se encuentra instantáneamente en reposo respecto a la manivela.
 [[Categoría:Problemas de movimiento plano (G.I.T.I.)]]

6.6. Disco en manivela ranurada

De Laplace

última version al 12:25 24 sep 2013

Contenido

1 Enunciado

2 Posición del CIR

3 Reducción cinemática

3.1 Directamente

3.1.1 Velocidad

3.1.2 Velocidad angular

3.1.3 Expresión de la reducción cinemática

3.2 Por composición de movimientos

3.2.1 Velocidad

3.2.2 Velocidad angular

4 Tipo de movimiento

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES