Segunda Convocatoria Ordinaria 2012/13 (G.I.A.)
De Laplace
(Página creada con '==Partícula sobre una circunferencia con un muelle== Una pequeña bolita <math>P </math> , de masa ,<math>m </m…') |
(→Partícula sobre una circunferencia con un muelle) |
||
| Línea 1: | Línea 1: | ||
==[[Ejercicio de dinámica de la partícula, Julio 2013 (F1 GIA)|Partícula sobre una circunferencia con un muelle]]== | ==[[Ejercicio de dinámica de la partícula, Julio 2013 (F1 GIA)|Partícula sobre una circunferencia con un muelle]]== | ||
| + | [[Imagen:GIA_particula_aro_muelle_enunciado.png|right]] | ||
Una pequeña bolita <math>P </math> , de masa ,<math>m </math> está insertada en un aro de centro <math>O </math> y radio ,<math>R </math> fijado en el plano vertical <math>OXY </math> .La partícula está sometida a la acción de la gravedad, que actúa en la dirección del eje <math>OX </math> <math>\vec{g}=g\,\vec{\imath} </math>, y a la de un resorte de longitud natural nula y constante recuperadora <math>k </math>, que tiene su otro extremo fijado en el punto del aro cuyas coordenadas son <math>A(-R,0,0) </math>. El rozamiento entre la bolita y el aro no es despreciable, estando caracterizado por un coeficiente de rozamiento cuyo valor <math>\mu </math> es prácticamente el mismo, tanto en el caso de equilibrio estático de la partícula, como cuando ́ésta se desplaza insertada en el aro. | Una pequeña bolita <math>P </math> , de masa ,<math>m </math> está insertada en un aro de centro <math>O </math> y radio ,<math>R </math> fijado en el plano vertical <math>OXY </math> .La partícula está sometida a la acción de la gravedad, que actúa en la dirección del eje <math>OX </math> <math>\vec{g}=g\,\vec{\imath} </math>, y a la de un resorte de longitud natural nula y constante recuperadora <math>k </math>, que tiene su otro extremo fijado en el punto del aro cuyas coordenadas son <math>A(-R,0,0) </math>. El rozamiento entre la bolita y el aro no es despreciable, estando caracterizado por un coeficiente de rozamiento cuyo valor <math>\mu </math> es prácticamente el mismo, tanto en el caso de equilibrio estático de la partícula, como cuando ́ésta se desplaza insertada en el aro. | ||
última version al 13:33 25 jul 2013
Partícula sobre una circunferencia con un muelle
Una pequeña bolita P , de masa ,m está insertada en un aro de centro O y radio ,R fijado en el plano vertical OXY .La partícula está sometida a la acción de la gravedad, que actúa en la dirección del eje OX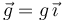 
, y a la de un resorte de longitud natural nula y constante recuperadora k, que tiene su otro extremo fijado en el punto del aro cuyas coordenadas son A( − R,0,0). El rozamiento entre la bolita y el aro no es despreciable, estando caracterizado por un coeficiente de rozamiento cuyo valor μ es prácticamente el mismo, tanto en el caso de equilibrio estático de la partícula, como cuando ́ésta se desplaza insertada en el aro.
Utilizando el ángulo θ para describir la posición de la partícula P..
- Obtenga la fuerza resultante (incluida la reacción vincular) que actúa sobre la partícula, expresada en el triedro intrínseco.
- Si los valores de los parámetros son tales que mg = kR, obtenga las expresiones matemáticas que definen las condiciones de equilibrio estático de la partícula y determine el rango de posiciones de equilibrio.
- Obtenga las ecuaciones que han de verificar en cada instante la velocidad y aceleración angulares,
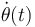y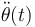 
. Considérese de nuevo el caso mg = kR y, además, que la partícula se encuentra inicialmente en la posición θ(t) = 0, con una velocidad angular inicial
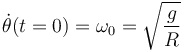
Para dicho instante inicial, determine los valores de la fuerza de reacción vincular, de la fuerza de rozamiento y de la aceleración angular.
