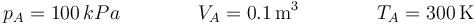Refrigerador que sigue un ciclo Otto
De Laplace
(→Esquema del ciclo) |
|||
| Línea 25: | Línea 25: | ||
(Este apartado puede hacerse combinado con el siguiente) | (Este apartado puede hacerse combinado con el siguiente) | ||
| - | El ciclo Otto posee una forma característica, por su | + | El ciclo Otto posee una forma característica, por su aplicación en los motores de explosión de gasolina. En su versión más ideal, está formado por dos adiabáticas y dos isócoras (curvas de volumen constante) |
Este sería el esquema del ciclo de un motor de explosión | Este sería el esquema del ciclo de un motor de explosión | ||
| Línea 35: | Línea 35: | ||
<center>[[Archivo:ciclo-otto-refrigerador.png]]</center> | <center>[[Archivo:ciclo-otto-refrigerador.png]]</center> | ||
| - | En el próximo apartado haremos una gráfica más precisa, aprovechando los valores numéricos, pero la idea es la siguiente. Tenemos el gas a temperatura ambiente. Al expandirlo rápidamente se enfría, cayendo su temperatura por debajo de la de la | + | En el próximo apartado haremos una gráfica más precisa, aprovechando los valores numéricos, pero la idea es la siguiente. Tenemos el gas a temperatura ambiente. Al expandirlo rápidamente se enfría, cayendo su temperatura por debajo de la de la habitación frigorífica, por lo que el calor pasará de la cámara al gas. Luego se comprime rápidamente, con lo que se calienta por encima de la temperatura exterior. Finalmente se expulsa calor al exterior, aprovechando esta diferencia de temperaturas, y se reinicia el ciclo. El resultado neto es que se está extrayendo calor del interior y expulsándolo al exterior. |
Cualquier representación del ciclo Otto en este problema como el de un motor es absurda y muestra que no se ha atendido a la mención explícita de “Ciclo Otto inverso” | Cualquier representación del ciclo Otto en este problema como el de un motor es absurda y muestra que no se ha atendido a la mención explícita de “Ciclo Otto inverso” | ||
==Presiones, volúmenes y temperaturas== | ==Presiones, volúmenes y temperaturas== | ||
| + | A continuación iremos construyendo una tabla de los diferentes valores de presiones, volúmenes y temperaturas. | ||
| + | |||
| + | El estado inicial del gas de la cámara es | ||
| + | |||
| + | <center><math>p_A = 100\,kPa\qquad\qquad V_A = 0.1\,\mathrm{m}^3\qquad\qquad T_A = 300\,\mathrm{K}</math></center> | ||
==Calores== | ==Calores== | ||
==Coeficiente de desempeño== | ==Coeficiente de desempeño== | ||
==Rendimiento de la segunda especie== | ==Rendimiento de la segunda especie== | ||
[[Categoría:Problemas de máquinas térmicas (GIE)]] | [[Categoría:Problemas de máquinas térmicas (GIE)]] | ||
Revisión de 20:29 21 jun 2013
Contenido |
1 Enunciado del ciclo
Se desea construir un refrigerador que funcione con un ciclo Otto inverso. Para ello se tiene una habitación cuya temperatura se desea mantener en 250K, estando el ambiente exterior a 300K y a una presión de 100kPa.
En una de las paredes de la habitación se instala la unidad refrigeradora, que experimenta el siguiente ciclo:

Inicialmente (estado A) una cámara de 0.1m³ está llena de aire (supuesto gas ideal) a la presión y temperatura exteriores, y aislada térmicamente del interior.
- A→B: La cámara se aísla del exterior y se expande rápidamente hasta un volumen de 0.2m³. Esta expansión se puede modelar como un proceso adiabático cuasiestático.
- B→C: Manteniendo el volumen fijo, se deja que intercambie calor con la habitación, hasta que la temperatura del aire de la cámara iguale a la de la habitación.
- C→D: La cámara se comprime rápidamente hasta volver a un volumen de 0.1m³. Esta compresión también se puede modelar como un proceso adiabático cuasiestático.
- D→A: Manteniendo el volumen fijo, se deja ahora que intercambie calor con el exterior, hasta que la temperatura del aire de la cámara iguale a la exterior.
Para este proceso cíclico:
- Represente de forma esquemática el ciclo en un diagrama pV.
- Calcule la presión, volumen y temperatura del gas en cada uno de los vértices del ciclo.
- Calcule el calor intercambiado por el aire con la habitación y con el exterior.
- Determine el coeficiente de desempeño COPR de este refrigerador.
- Calcule la proporción entre este coeficiente de desempeño y el máximo que podría alcanzar un refrigerador que operara entre las temperaturas indicadas.
Datos: Constante de los gases ideales: 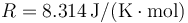 , Relación entre capacidades caloríficas del aire γ = 1.4.
, Relación entre capacidades caloríficas del aire γ = 1.4.
2 Esquema del ciclo
(Este apartado puede hacerse combinado con el siguiente)
El ciclo Otto posee una forma característica, por su aplicación en los motores de explosión de gasolina. En su versión más ideal, está formado por dos adiabáticas y dos isócoras (curvas de volumen constante)
Este sería el esquema del ciclo de un motor de explosión
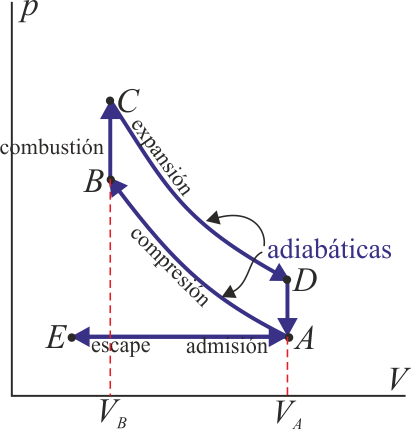 (INCORRECTO)
(INCORRECTO)Sin embargo, este no puede ser el ciclo de nuestro problema, ya que esta gráfica describe un motor, es decir un dispositivo que transforma calor en trabajo. Este problema trata sobre un refrigerador, es decir, un dispositivo que absorbe una cierta cantidad de trabajo para extraer calor y expulsarlo al exterior. Gráficamente, quiere decir que en un motor el recorrido del ciclo es en sentido horario, pero en un refrigerador es antihorario, así que el esquema correcto debe ser algo así:
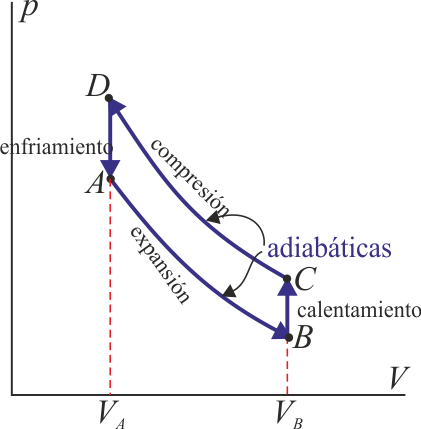
En el próximo apartado haremos una gráfica más precisa, aprovechando los valores numéricos, pero la idea es la siguiente. Tenemos el gas a temperatura ambiente. Al expandirlo rápidamente se enfría, cayendo su temperatura por debajo de la de la habitación frigorífica, por lo que el calor pasará de la cámara al gas. Luego se comprime rápidamente, con lo que se calienta por encima de la temperatura exterior. Finalmente se expulsa calor al exterior, aprovechando esta diferencia de temperaturas, y se reinicia el ciclo. El resultado neto es que se está extrayendo calor del interior y expulsándolo al exterior.
Cualquier representación del ciclo Otto en este problema como el de un motor es absurda y muestra que no se ha atendido a la mención explícita de “Ciclo Otto inverso”
3 Presiones, volúmenes y temperaturas
A continuación iremos construyendo una tabla de los diferentes valores de presiones, volúmenes y temperaturas.
El estado inicial del gas de la cámara es