Fuerza entre dos varillas colineales
De Laplace
(Nueva página: ==Enunciado== Calcule la fuerza entre dos varillas colineales, de longitudes <math>L_1</math> y <math>L_2</math>, que almacenan respectivamente cargas <math>Q_1</math> y <math>Q_2</ma...) |
(→Solución) |
||
| Línea 3: | Línea 3: | ||
==Solución== | ==Solución== | ||
| + | la fuerza sobre una distribución de carga que almacena una carga total <math>Q</math>, '''no''' es igual al producto de la carga por el campo | ||
| + | |||
| + | <center><math>\mathbf{F}\neq Q\mathbf{E}</math></center> | ||
| + | |||
| + | ya que esta expresión solo vale para cargas puntuales. En particular, ¿qué es <math>\mathbf{E}</math>? ¿El campo en un extremo de la varilla, en el otro, en su punto medio? | ||
| + | |||
| + | La expresión correcta para la fuerza neta sobre un sistema es, como ocurre generalmente en mecánica, la ''resultante'' de las fuerzas aplicadas, esto es, la suma vectorial de las fuerzas aplicadas sobre cada punto de la distribución. | ||
| + | |||
| + | Dividiendo una distribución en elementos de volumen, cada uno de los cuales se puede suponer puntual, queda | ||
| + | |||
| + | <center><math>\mathbf{F}= \int mathrm{d}q\,\mathbf{(\mathbf{r}')=\int \rho(\mathbf{r}')\,\mathbf{(\mathbf{r}')\mathrm{d}\tau'</math></center> | ||
| + | |||
| + | |||
[[Categoría:Problemas de electrostática en el vacío]] | [[Categoría:Problemas de electrostática en el vacío]] | ||
Revisión de 09:07 26 nov 2008
1 Enunciado
Calcule la fuerza entre dos varillas colineales, de longitudes L1 y L2, que almacenan respectivamente cargas Q1 y Q2, cuando sus extremos más próximos distan una cantidad a.
2 Solución
la fuerza sobre una distribución de carga que almacena una carga total Q, no es igual al producto de la carga por el campo
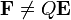
ya que esta expresión solo vale para cargas puntuales. En particular, ¿qué es 
? ¿El campo en un extremo de la varilla, en el otro, en su punto medio?
La expresión correcta para la fuerza neta sobre un sistema es, como ocurre generalmente en mecánica, la resultante de las fuerzas aplicadas, esto es, la suma vectorial de las fuerzas aplicadas sobre cada punto de la distribución.
Dividiendo una distribución en elementos de volumen, cada uno de los cuales se puede suponer puntual, queda
