Sistema de tres superficies esféricas cargadas

De Laplace

(Diferencias entre revisiones)

Revisión de 23:54 30 abr 2013

Contenido

1 Enunciado
2 Campo eléctrico
3 Caso general

1 Enunciado

Supongamos un sistema formado por tres superficies esféricas concéntricas, de radios $R 1 = 2 a$ , $R 2 = 3 a$ y $R 3 = 6 a$ , respectivamente, que almacenan cargas $Q 1$ , $Q 2$ y $Q 3$ distribuidas uniformemente en cada una.

Calcule

El campo eléctrico en todos los puntos del espacio.
El trabajo necesario para llevar una carga $q 0$ desde el infinito hasta el centro del sistema.
La energía electrostática almacenada en el sistema de tres esferas (sin incluir la carga $q 0$ ).

para cada uno de los siguientes tres casos:

$Q 1 = Q 2 = Q 0$ , $Q 3 = - 2 Q 0$ .
$Q 1 = Q 3 = Q 0$ , $Q 2 = - 2 Q 0$ .
$Q 2 = Q 3 = Q 0$ , $Q 1 = - 2 Q 0$ .

2 Campo eléctrico

3 Caso general

En lugar de resolver tres veces el mismo problema, consideramos un sistema con cargas cualesquiera y posteriormente sustituimos por sus valores concretos.

El campo debido a las tres esferas, se calcula por aplicación de la ley de Gauss. Por la simetría esférica del sistema, el campo es radial y dependiente solo de la distancia al centro del sistema

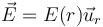
$\vec{E}=E(r)\vec{u}_r$

Para cada superficie esférica que tomemos

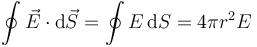
$\oint \vec{E}\cdot\mathrm{d}\vec{S}=\oint E\,\mathrm{d}S = 4\pi r^2E$

De acuerdo con la ley de Gauss

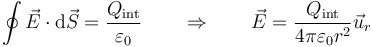
$\oint \vec{E}\cdot\mathrm{d}\vec{S}=\frac{Q_\mathrm{int}}{\varepsilon_0}\qquad\Rightarrow\qquad \vec{E}=\frac{Q_\mathrm{int}}{4\pi \varepsilon_0 r^2}\vec{u}_r$

Tenemos ahora cuatro regiones, de adentro a fuera:

r < 2a: En el interior de la esfera pequeña no se envuelve ninguna carga, por lo que el campo es nulo

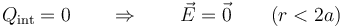
$Q_\mathrm{int}=0\qquad\Rightarroçw\qquad \vec{E}=\vec{0}\qquad (r< 2a)$

2a < r < 3a: Entre la esfera pequeña y la intermedia se envuelve a la esfera pequeña, con carga $Q 1$

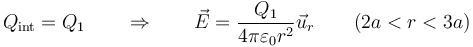
$Q_\mathrm{int}=Q_1\qquad\Rightarroçw\qquad \vec{E}=\frac{Q_1}{4\pi \varepsilon_0 r^2}\vec{u}_r\qquad (2a < r < 3a)$

3a < r < 6a: Entre la esfera intermedia y la grande se envuelve tanto a la esfera pequeña como a la intermedia

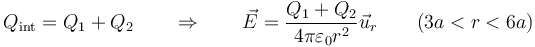
$Q_\mathrm{int}=Q_1+Q_2\qquad\Rightarroçw\qquad \vec{E}=\frac{Q_1+Q_2}{4\pi \varepsilon_0 r^2}\vec{u}_r\qquad (3a < r < 6a)$

6a<r: En el exterior de la esfera grande se envuelve a las tres esferas

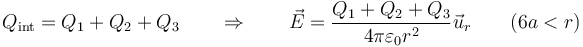
$Q_\mathrm{int}=Q_1+Q_2+Q_3\qquad\Rightarroçw\qquad \vec{E}=\frac{Q_1+Q_2+Q_3}{4\pi \varepsilon_0 r^2}\vec{u}_r\qquad (6a < r)$

Ahora bien, en los tres casos prácticos, la suma de las tres cargas es cero, así que

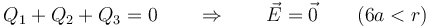
$Q_1 + Q_2 + Q_3 = 0 \qquad\Rightarroçw\qquad \vec{E}=\vec{0}\qquad (6a< r)$

Reuniendo los cuatro resultados

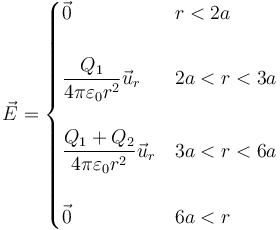
$\vec{E}=\begin{cases} \vec{0} & r < 2a \\ & \\ \displaystyle \frac{Q_1}{4\pi \varepsilon_0 r^2}\vec{u}_r & 2a <r < 3a \\ & \\ \displaystyle \frac{Q_1+Q_2}{4\pi \varepsilon_0 r^2}\vec{u}_r & 3a <r < 6a \\ & \\ \vec{0} & 6a < r\end{cases}$

3.1 Primer caso

Sustituimos ahora los valores de $Q 1$ y $Q 2$ . En el primer caso

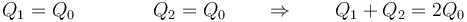
$Q_1 = Q_0\qquad\qquad Q_2=Q_0\qquad\Rightarrow\qquad Q_1+Q_2=2Q_0$

lo que nos da el nuevo campo

$\vec{E}=\begin{cases} \vec{0} & r < 2a \\ & \\ \displaystyle \frac{Q_0}{4\pi \varepsilon_0 r^2}\vec{u}_r & 2a <r < 3a \\ & \\ \displaystyle \frac{2Q_0}{4\pi \varepsilon_0 r^2}\vec{u}_r & 3a <r < 6a \\ & \\ \vec{0} & 6a < r\end{cases}$

El campo va hacia afuera en las dos regiones en que no es nulo.

3.2 Segundo caso

En el segundo caso

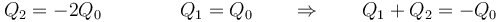
$Q_2 = -2Q_0\qquad\qquad Q_1=Q_0\qquad\Rightarrow\qquad Q_1+Q_2=-Q_0$

lo que nos da el nuevo campo

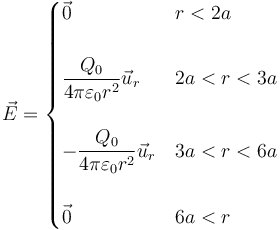
$\vec{E}=\begin{cases} \vec{0} & r < 2a \\ & \\ \displaystyle \frac{Q_0}{4\pi \varepsilon_0 r^2}\vec{u}_r & 2a <r < 3a \\ & \\ \displaystyle -\frac{Q_0}{4\pi \varepsilon_0 r^2}\vec{u}_r & 3a <r < 6a \\ & \\ \vec{0} & 6a < r\end{cases}$

En la región entre la esfera intermedia y la exterior va ahora hacia adentro.

3.3 Tercer caso

Por último

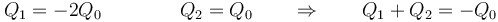
$Q_1 = -2Q_0\qquad\qquad Q_2=Q_0\qquad\Rightarrow\qquad Q_1+Q_2=-Q_0$

lo que nos da el campo

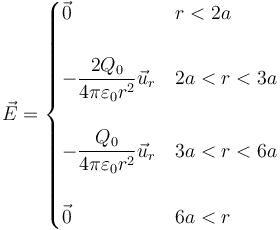
$\vec{E}=\begin{cases} \vec{0} & r < 2a \\ & \\ \displaystyle -\frac{2Q_0}{4\pi \varepsilon_0 r^2}\vec{u}_r & 2a <r < 3a \\ & \\ \displaystyle -\frac{Q_0}{4\pi \varepsilon_0 r^2}\vec{u}_r & 3a <r < 6a \\ & \\ \vec{0} & 6a < r\end{cases}$

En este caso el campo va ahora hacia adentro en las dos regiones en que no es nulo.

@@ Línea 56: / Línea 56: @@
 <center><math>\vec{E}=\begin{cases} \vec{0} &  r < 2a \\ & \\ \displaystyle \frac{Q_1}{4\pi \varepsilon_0 r^2}\vec{u}_r & 2a <r < 3a \\ & \\ \displaystyle \frac{Q_1+Q_2}{4\pi \varepsilon_0 r^2}\vec{u}_r & 3a <r < 6a \\ & \\ \vec{0} &  6a < r\end{cases}</math></center>
-==Primer caso==
+===Primer caso===
-==Segundo caso==
+Sustituimos ahora los valores de <math>Q_1</math> y <math>Q_2</math>. En el primer caso
-==Tercer caso==
+<center><math>Q_1 = Q_0\qquad\qquad Q_2=Q_0\qquad\Rightarrow\qquad Q_1+Q_2=2Q_0</math></center>
+lo que nos da el nuevo campo
+<center><math>\vec{E}=\begin{cases} \vec{0} &  r < 2a \\ & \\ \displaystyle \frac{Q_0}{4\pi \varepsilon_0 r^2}\vec{u}_r & 2a <r < 3a \\ & \\ \displaystyle \frac{2Q_0}{4\pi \varepsilon_0 r^2}\vec{u}_r & 3a <r < 6a \\ & \\ \vec{0} &  6a < r\end{cases}</math></center>
+El campo va hacia afuera en las dos regiones en que no es nulo.
+===Segundo caso===
+En el segundo caso
+<center><math>Q_2 = -2Q_0\qquad\qquad Q_1=Q_0\qquad\Rightarrow\qquad Q_1+Q_2=-Q_0</math></center>
+lo que nos da el nuevo campo
+<center><math>\vec{E}=\begin{cases} \vec{0} &  r < 2a \\ & \\ \displaystyle \frac{Q_0}{4\pi \varepsilon_0 r^2}\vec{u}_r & 2a <r < 3a \\ & \\ \displaystyle -\frac{Q_0}{4\pi \varepsilon_0 r^2}\vec{u}_r & 3a <r < 6a \\ & \\ \vec{0} &  6a < r\end{cases}</math></center>
+En la región entre la esfera intermedia y la exterior va ahora hacia adentro.
+===Tercer caso===
+Por último
+<center><math>Q_1 = -2Q_0\qquad\qquad Q_2=Q_0\qquad\Rightarrow\qquad Q_1+Q_2=-Q_0</math></center>
+lo que nos da el campo
+<center><math>\vec{E}=\begin{cases} \vec{0} &  r < 2a \\ & \\ \displaystyle -\frac{2Q_0}{4\pi \varepsilon_0 r^2}\vec{u}_r & 2a <r < 3a \\ & \\ \displaystyle -\frac{Q_0}{4\pi \varepsilon_0 r^2}\vec{u}_r & 3a <r < 6a \\ & \\ \vec{0} &  6a < r\end{cases}</math></center>
+En este caso el campo va ahora hacia adentro en las dos regiones en que no es nulo.
 [[Categoría:Problemas de electrostática en el vacío (GIE)]]

Sistema de tres superficies esféricas cargadas

De Laplace

Revisión de 23:54 30 abr 2013

Contenido

1 Enunciado

2 Campo eléctrico

3 Caso general

3.1 Primer caso

3.2 Segundo caso

3.3 Tercer caso

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES