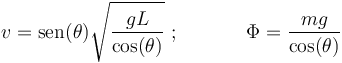No Boletín - Péndulo cónico (Ex.Ene/13)
De Laplace
(Página creada con '==Enunciado== right Se denomina péndulo cónico a un péndulo simple cuya masa puntual, en lugar de oscilar en un plano vertical, realiza un mov…') |
(→Solución) |
||
| (7 ediciones intermedias no se muestran.) | |||
| Línea 6: | Línea 6: | ||
# ¿Con qué celeridad se mueve la masa puntual? | # ¿Con qué celeridad se mueve la masa puntual? | ||
# ¿Cuál es el módulo de la tensión del hilo? | # ¿Cuál es el módulo de la tensión del hilo? | ||
| + | |||
| + | ==Solución== | ||
| + | [[Archivo:pendulo-conico-sol.png|right]] | ||
| + | |||
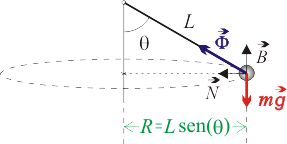
| + | La masa puntual describe con celeridad constante <math>v\,</math> (movimiento uniforme) una circunferencia de radio: | ||
| + | <center><math> | ||
| + | R=L\,\mathrm{sen}(\theta) | ||
| + | </math></center> | ||
| + | y lo hace bajo la acción de dos fuerzas: el peso <math>m\vec{g}\,</math> y la tensión ejercida por el hilo <math>\vec{\Phi}\,</math>. | ||
| + | |||
| + | Para expresar las magnitudes vectoriales, utilizaremos el triedro intrínseco <math>\{\vec{T},\vec{N},\vec{B}\}\,</math> de la circunferencia. | ||
| + | |||
| + | El peso es una fuerza activa y, como tal, es conocida a priori: | ||
| + | <center><math> | ||
| + | m\vec{g}=-mg\,\vec{B} | ||
| + | </math></center> | ||
| + | Sin embargo, la tensión del hilo es una fuerza de reacción vincular, de módulo <math>\Phi\,</math> en principio desconocido, con dirección a lo largo del hilo y sentido hacia el punto de suspensión del hilo: | ||
| + | <center><math> | ||
| + | \vec{\Phi}=\Phi[\,\mathrm{sen}(\theta)\,\vec{N}+\mathrm{cos}(\theta)\,\vec{B}\,] | ||
| + | </math></center> | ||
| + | |||
| + | Dado que la masa puntual describe un movimiento circular uniforme, sabemos que su aceleración sólo va a tener componente normal: | ||
| + | <center><math> | ||
| + | \left.\begin{array}{l} a_t=\displaystyle\frac{dv}{dt}=0 \\ \\ a_n=\displaystyle\frac{v^2}{R}=\frac{v^2}{L\,\mathrm{sen}(\theta)} \end{array}\right\} \,\,\,\,\,\longrightarrow\,\,\,\,\, \vec{a}=a_t\,\vec{T}+a_n\,\vec{N}=\displaystyle\frac{v^2}{L\,\mathrm{sen}(\theta)}\,\vec{N} | ||
| + | </math></center> | ||
| + | |||
| + | Aplicando la segunda ley de Newton, y separando componentes, se llega al siguiente sistema de ecuaciones (para las incógnitas <math>v\,</math> y <math>\Phi\,</math>): | ||
| + | <center><math> | ||
| + | m\vec{g}+\vec{\Phi}=m\vec{a}\,\,\,\,\,\longrightarrow\,\,\,\,\,\left\{\begin{array}{l} \Phi\,\mathrm{sen}(\theta)=m\displaystyle\frac{v^2}{L\,\mathrm{sen}(\theta)} \\ \\ -mg+\Phi\,\mathrm{cos}(\theta)=0 \end{array}\right. | ||
| + | </math></center> | ||
| + | Resolviendo el sistema, obtenemos los valores de la celeridad <math>v\,</math> de la partícula y del módulo <math>\Phi\,</math> de la tensión del hilo: | ||
| + | <center><math> | ||
| + | v=\mathrm{sen}(\theta)\sqrt{\frac{gL}{\mathrm{cos}(\theta)}}\,\,;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, | ||
| + | \Phi=\frac{mg}{\mathrm{cos}(\theta)} | ||
| + | </math></center> | ||
[[Categoría:Problemas de dinámica del punto material (G.I.T.I.)]] | [[Categoría:Problemas de dinámica del punto material (G.I.T.I.)]] | ||
última version al 14:00 6 mar 2013
1 Enunciado
Se denomina péndulo cónico a un péndulo simple cuya masa puntual, en lugar de oscilar en un plano vertical, realiza un movimiento circular uniforme en un plano horizontal (ver figura). Considere que la masa puntual es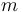 
, la longitud del péndulo es 
, el ángulo que forma el hilo con la vertical es 
y la gravedad es 
.
- ¿Con qué celeridad se mueve la masa puntual?
- ¿Cuál es el módulo de la tensión del hilo?
2 Solución
La masa puntual describe con celeridad constante 
(movimiento uniforme) una circunferencia de radio:
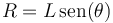
y lo hace bajo la acción de dos fuerzas: el peso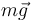 
y la tensión ejercida por el hilo 
.
Para expresar las magnitudes vectoriales, utilizaremos el triedro intrínseco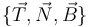 
de la circunferencia.
El peso es una fuerza activa y, como tal, es conocida a priori:
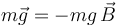
Sin embargo, la tensión del hilo es una fuerza de reacción vincular, de módulo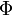 
en principio desconocido, con dirección a lo largo del hilo y sentido hacia el punto de suspensión del hilo:
![\vec{\Phi}=\Phi[\,\mathrm{sen}(\theta)\,\vec{N}+\mathrm{cos}(\theta)\,\vec{B}\,]](/wiki/images/math/c/c/7/cc7b21a1b7dc0d599c0f60bf82eae40b.png)
Dado que la masa puntual describe un movimiento circular uniforme, sabemos que su aceleración sólo va a tener componente normal:
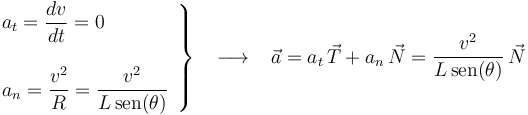
Aplicando la segunda ley de Newton, y separando componentes, se llega al siguiente sistema de ecuaciones (para las incógnitas y ):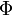
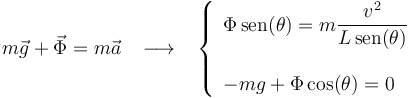
Resolviendo el sistema, obtenemos los valores de la celeridad de la partícula y del módulo 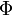de la tensión del hilo:
