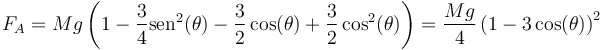Movimiento de una barra apoyada
De Laplace
(→Reacción en el suelo) |
|||
| Línea 197: | Línea 197: | ||
<center><math>F_A = Mg + M\frac{H}{2}\left(-\left(\frac{3g}{2H}\mathrm{sen}(\theta)\right)\,\mathrm{sen}(\theta)-\left(\frac{3g}{H}(1-\cos(\theta))\right)\cos(\theta)\right)</math></center> | <center><math>F_A = Mg + M\frac{H}{2}\left(-\left(\frac{3g}{2H}\mathrm{sen}(\theta)\right)\,\mathrm{sen}(\theta)-\left(\frac{3g}{H}(1-\cos(\theta))\right)\cos(\theta)\right)</math></center> | ||
| + | |||
| + | Desarrollando | ||
| + | |||
| + | <center><math>F_A = Mg\left(1-\frac{3}{4}\mathrm{sen}^2(\theta)-\frac{3}{2}\cos(\theta)+\frac{3}{2}\cos^2(\theta)\right) = \frac{Mg}{4}\left(1-3\cos(\theta)\right)^2</math></center> | ||
==Separación de la pared== | ==Separación de la pared== | ||
[[Categoría:Problemas de dinámica del sólido rígido (GIE)]] | [[Categoría:Problemas de dinámica del sólido rígido (GIE)]] | ||
Revisión de 12:25 12 ene 2013
Contenido |
1 Enunciado
En el mismo sistema del problema “Equilibrio de una barra apoyada”, considérese el caso en que no hay rozamiento ni con la pared ni con el suelo. Si la barra se encuentra inicialmente en la posición vertical y por una pequeña perturbación comienza a deslizarse resbalando por el suelo y la pared:
- ¿Cuál es la ecuación de movimiento para el ángulo θ que forma la barra con la pared?
- ¿Cuánto valen las fuerzas que ejercen la pared y el suelo para cada posición de la barra?
- ¿Llega a separarse en algún momento de la pared? ¿Para qué ángulo?
2 Ecuación de movimiento
2.1 Planteamiento
La barra, al descender, va variando el ángulo que forma con la pared, que va aumentando progresivamente. El movimiento de la barra está gobernado por tres fuerzas:
- Su peso, aplicado en su centro de masas, que se halla en el centro de la barra, y que apunta en la dirección vertical hacia abajo.
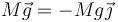
- La fuerza de reacción del suelo, aplicada en el punto A, donde se apoya la barra. Al no haber rozamiento, esta fuerza es puramente perpendicular a la superficie
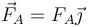
- La fuerza de reacción de la pared, aplicada en el punto B, donde se apoya la barra. Puesto que aquí tampoco hay rozamiento, apunta en la dirección perpendicular, que ahora es horizontal
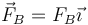
La magnitud de estas dos fuerzas es desconocida, por lo que se trata de incógnitas adicionales del problema.
Por semejanza de triángulos, si la posición instantánea del centro de masas es
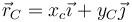
la de los puntos de contacto es

A su vez, estas posiciones se relacionan con el ángulo θ por
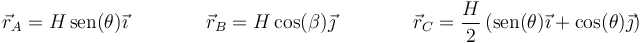
Las ecuaciones que gobiernan el movimiento de la barra son:
- Teorema de la cantidad de movimiento
- La masa por la aceleración del centro de masas es igual a la resultante de todas las fuerzas externas aplicadas
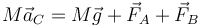
Separando por componentes

- Teorema del momento cinético
- La derivada del momento cinético respecto al centro de masas es igual al momento resultante respecto a este punto de las fuerzas externas aplicadas.
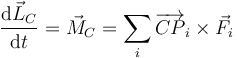
- En este caso, el peso no tiene momento, por estar aplicado en el propio CM y las dos fuerzas de reacciones producen giros en sentidos opuestos. Tanto el momento cinético como los momentos de las fuerzas van en la dirección de
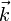 por lo que podemos escribir
por lo que podemos escribir
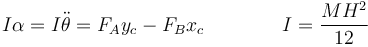
Tenemos entonces tres ecuaciones con cinco incógnitas (las dos componentes de la aceleración lineal, la aceleración angular y las dos fuerzas de reacción)
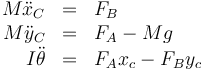
Para completar estas dos ecuaciones añadimos las condiciones de vínculo, que relacionan las tres variables
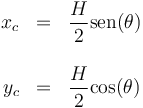
Este sistema de cinco ecuaciones se puede resolver completamente y más adelante veremos cómo se hace. No obstante, ante de exponer esa solución, consideraremos un atajo basado en hacer uso de la conservación de la energía mecánica.
2.2 Solución empleando la energía mecánica
El teorema de la energía mecánica para un sólido nos dice que
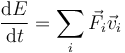
siendo E la energía mecánica, que en este caso vale
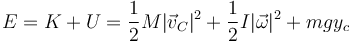
y el segundo término representa la potencia de las fuerzas externas no conservativas aplicadas, que en este problema son las dos fuerzas de reacción (el peso ya ha sido considerado al incluir la energía potencial).
Ahora bien, las fuerzas de reacción son perpendiculares a las superficies, mientras que las velocidades de los puntos de contacto son tangentes a ellas, por lo que
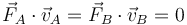
Esto quiere decir que estas fuerzas no realizan trabajo y la energía mecánica se conserva

Esta ecuación nos resuelve completamente el problema. Calculamos en primer lugar la energía cinética de traslación
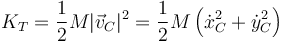
donde las componentes de la velocidad del CM valen

Esto nos da la energía cinética de traslación
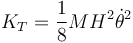
La de rotación se obtiene directamente
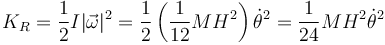
Sumando las dos cantidades queda
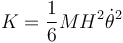
La energía potencial la da la altura del centro de masas

La suma de la energía cinética y la potencial nos da la energía mecánica
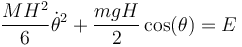
El valor de la energía mecánica, que es constante, lo obtenemos particularizando para el estado inicial. Si al principio la barra está en reposo y prácticamente vertical
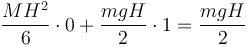
lo que nos da la ley de conservación de la energía
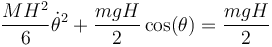
A partir de aquí, podemos determinar completamente el movimiento. Despejando el cuadrado de la velocidad angular
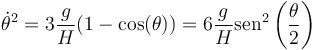
Tomando la raíz cuadrada hallamos la velocidad angular
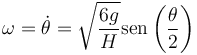
De aquí se puede integrar el ángulo como función del tiempo, por ser la ecuación separable
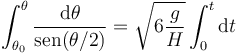
Calculando las integrales y despejando se obtiene θ = θ(t)
Alternativamente, podemos derivar la velocidad angular respecto al tiempo, para hallar la aceleración angular
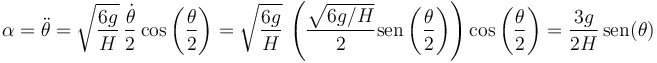
2.3 Solución sin usar la energía
Si no estamos seguros de si la energía se conserva o no, el método anterior puede parecer inadecuado. En ese caso, siempre podemos determinar la ecuación de movimiento a partir del teorema de la cantidad de movimiento y del del momento cinético.
La forma de hacerlo es reducir el sistema de ecuaciones para xC, yC y θ (junto con las fuerzas de reacción, en uno para θ y sus derivadas.
En primer lugar, despejamos las fuerzas de reacción

y sustituimos en la ecuación del momento cinético
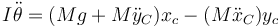
Ya hemos eliminado las fuerzas. Ahora queda escribir xC e yC en función de θ. Para ello, necesitamos hallar la primera derivada respecto al tiempo, que ya conocemos,

y la segunda derivada respecto al tiempo, aplicando reiteradamente la regla de la cadena.

Sustituyendo en el teorema del momento cinético queda
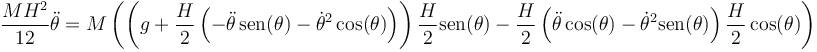
Afortunadamente, cuando se quitan paréntesis, esta expresión se simplifica notablemente
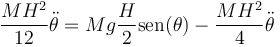
y agrupando términos obtenemos la ecuación de movimiento

que por supuesto coincide con la que obtuvimos a partir de la ley de conservación de la energía mecánica.
Esta ecuación puede ser integrada una vez respecto al tiempo. Multiplicando por 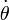 e integrando conseguimos la ecuación que también obtuvimos en el otro método de solución:
e integrando conseguimos la ecuación que también obtuvimos en el otro método de solución:

3 Fuerzas de reacción
Una vez que tenemos la primera y la segunda derivada del ángulo respecto al tiempo, como función del ángulo, podemos hallar las fuerzas de reacción de cada punto.
3.1 Reacción en el suelo
Esta fuerza es igual a
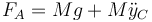
Sustituyendo la componente vertical de la aceleración del CM
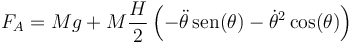
y sustituyendo aquí la primera y la segunda derivada del ángulo
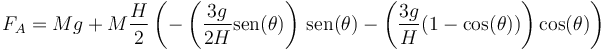
Desarrollando