Movimiento de una barra apoyada
De Laplace
(Diferencias entre revisiones)
(→Ecuación de movimiento) |
|||
| Línea 18: | Línea 18: | ||
<center><math>\vec{F}_A=F_A\vec{\jmath}</math></center> | <center><math>\vec{F}_A=F_A\vec{\jmath}</math></center> | ||
| - | * La fuerza de reacción de la | + | * La fuerza de reacción de la pared, aplicada en el punto B, donde se apoya la barra. Puesto que aquí tampoco hay rozamiento, apunta en la dirección perpendicular, que ahora es horizontal |
<center><math>\vec{F}_B=F_B\vec{\imath}</math></center> | <center><math>\vec{F}_B=F_B\vec{\imath}</math></center> | ||
| + | |||
| + | La magnitud de estas dos fuerzas es desconocida, por lo que se trata de incógnitas adicionales del problema. | ||
| + | |||
| + | Por semejanza de triángulos, si la posición instantánea del centro de masas es | ||
| + | |||
| + | <center><math>\vec{r}_C = x_c\vec{\imath}+y_C\vec{\jmath}</math></center> | ||
| + | |||
| + | la de los puntos de contacto es | ||
| + | |||
| + | <center><math>\vec{r}_A=2x_C\vec{\imath}\qquad\qquad \vec{r}_B = 2y_C\vec{\jmath}</math></center> | ||
| + | |||
| + | A su vez, estas posiciones se relacionan con el ángulo θ por | ||
| + | |||
| + | <center><math>\vec{r}_A=H\,\mathrm{sen}(\theta)\vec{\imath}\qquad\qquad \vec{r}_B=H\cos(\beta)\vec{\jmath}\qquad\qquad\vec{r}_C=\frac{H}{2}\left(\mathrm{sen}(\theta)\vec{\imath}+\cos(\theta)\vec{\math}\right)</math></center> | ||
===Solución empleando la energía mecánica=== | ===Solución empleando la energía mecánica=== | ||
===Solución sin usar la energía=== | ===Solución sin usar la energía=== | ||
| + | |||
==Fuerzas de reacción== | ==Fuerzas de reacción== | ||
==Separación de la pared== | ==Separación de la pared== | ||
[[Categoría:Problemas de dinámica del sólido rígido (GIE)]] | [[Categoría:Problemas de dinámica del sólido rígido (GIE)]] | ||
Revisión de 11:00 11 ene 2013
Contenido |
1 Enunciado
En el mismo sistema del problema “Equilibrio de una barra apoyada”, considérese el caso en que no hay rozamiento ni con la pared ni con el suelo. Si la barra se encuentra inicialmente en la posición vertical y por una pequeña perturbación comienza a deslizarse resbalando por el suelo y la pared:
- ¿Cuál es la ecuación de movimiento para el ángulo θ que forma la barra con la pared?
- ¿Cuánto valen las fuerzas que ejercen la pared y el suelo para cada posición de la barra?
- ¿Llega a separarse en algún momento de la pared? ¿Para qué ángulo?
2 Ecuación de movimiento
2.1 Planteamiento
La barra, al descender, va variando el ángulo que forma con la pared, que va aumentando progresivamente. El movimiento de la barra está gobernado por tres fuerzas:
- Su peso, aplicado en su centro de masas, que se halla en el centro de la barra, y que apunta en la dirección vertical hacia abajo.
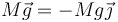
- La fuerza de reacción del suelo, aplicada en el punto A, donde se apoya la barra. Al no haber rozamiento, esta fuerza es puramente perpendicular a la superficie
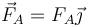
- La fuerza de reacción de la pared, aplicada en el punto B, donde se apoya la barra. Puesto que aquí tampoco hay rozamiento, apunta en la dirección perpendicular, que ahora es horizontal
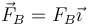
La magnitud de estas dos fuerzas es desconocida, por lo que se trata de incógnitas adicionales del problema.
Por semejanza de triángulos, si la posición instantánea del centro de masas es
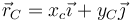
la de los puntos de contacto es

A su vez, estas posiciones se relacionan con el ángulo θ por





