Primera Convocatoria Ordinaria 2011/12 (G.I.A.)

De Laplace

Revisión de 11:33 25 feb 2012 (ver código fuente) Gabriel (Discusión | contribuciones) (→Cuestión sobre teoremas de conservación) ← Edición más antigua		última version al 18:34 8 ene 2013 (ver código fuente) Gabriel (Discusión | contribuciones) (→Barra inscrita en un triángulo)
(3 ediciones intermedias no se muestran.)
Línea 7:		Línea 7:
	==[[Ejercicio_de_Dinámica_del_Punto,_F1_GIA_(Enero,_2012)|Partícula en tubo con resortes]]==		==[[Ejercicio_de_Dinámica_del_Punto,_F1_GIA_(Enero,_2012)|Partícula en tubo con resortes]]==
		+	[[Archivo:f1_gia_1aconv_11_12_P1_0.gif|right]]Un tubo estrecho <math>AB</math> de longitud <math>2l</math> y de masa despreciable, contenido en todo instante en el plano horizontal fijo <math>OXY</math>, gira con velocidad angular constante alrededor de su centro <math>O</math>, de manera que el ángulo que forma el tubo con la dirección <math>OX</math> verifica la ley horaria <math>\theta(t)=\omega\!\ t</math>. En el interior del tubo hay una partícula <math>P</math> de masa <math>m</math>, que puede moverse sin rozamiento apreciable. Sendos resortes ideales, ambos de longitud natural nula y constante recuperadora de valor <math>k</math>, conectan la partícula con los extremos <math>A</math> y <math>B</math> del tubo.
		+
		+	# Escriba las expresiones de los vectores posición, velocidad y aceleración de la partícula en función de la variable <math>r</math> y sus derivadas, utilizando la base de las coordenadas polares <math>\{\vec{u}_r\mathrm{,}\vec{u}_\theta\}</math>. Exprese también las distintas fuerzas que actúan sobre la partícula.
		+	# Aplique las leyes de la Dinámica para formular las ecuaciones de movimiento del sistema. A la vista de la ecuación  diferencial que describe el comportamiento de <math>r(t)</math>, indique el tipo de movimiento que realiza la partícula a lo largo del tubo para los siguientes casos: (a) <math>\displaystyle\omega=\omega_0</math>; {{quad}} (b) <math>\omega=\sqrt{2}\!\ \omega_0</math>, y (c) <math>\omega=\sqrt{3}\!\ \omega_0</math>, siendo <math>\omega_0=\sqrt{k/m}</math>.
		+	# Considérese la situación particular en que el valor de la velocidad angular es <math>\omega=\sqrt{2}\!\ \omega_0</math> -caso (b)-, y en el instante inicial (<math>t=0</math>) la partícula se halla en el punto <math>O</math> con una velocidad cuyo módulo vale <math>v_0</math>. Obtenga la ley horaria para la variable <math>r(t)</math>, así como la fuerza de reacción vincular que actúa sobre la partícula.
		+	# Obtenga la expresión horaria <math>E(t)</math> para la energía mecánica de la partícula ¿Se conserva <math>E(t)</math>? ¿Por qué?
	==[[Ejercicio_de_cinemática_del_sólido,Primera_Convocatoria_Ordinaria_Enero_2012|Barra inscrita en un triángulo]]==		==[[Ejercicio_de_cinemática_del_sólido,Primera_Convocatoria_Ordinaria_Enero_2012|Barra inscrita en un triángulo]]==
		+	Los extremos <math>A</math> y <math>B</math> de una barra de longitud <math>L</math> (sólido &ldquo;2&rdquo;), están obligados a moverse por sendos lados desiguales de un triángulo rectángulo isósceles (sólido &ldquo;1&rdquo;). Partiendo del punto <math>O</math>, el extremo <math>A</math> se desliza por el lado <math>OC</math>, también de longitud <math>L</math>, con velocidad constante de módulo <math>v_0</math>. El extremo <math>B</math> se desliza por el lado <math>OD</math> de longitud <math>\sqrt{2}\!\ L</math>. Para indicar la posición de la barra en el sistema se sugiere utilizar el ángulo <math>\theta</math> mostrado en la figura.
		+
		+	[[Archivo:f1_gia_1aconv_11_12_P2_0.gif|right]]
		+
		+	# Determine la posición del C.I.R. (punto <math>I_{21}</math>) y una reducción cinemática del movimiento {21}, en función del valor del ángulo <math>\theta</math>.
		+	# Obtenga las derivadas con respecto al tiempo de los vectores de la reducción. Calcule la velocidad y la aceleración instantánea del extremo <math>B</math> en las posiciones inicial y final (extremo <math>A</math> en los puntos <math>O</math> y <math>C</math>, respectivamente).
		+	# Obtenga la expresión paramétrica de la trayectoria seguida por <math>I_{21}</math> y la distancia entre este punto y <math>O</math>, en función del valor del ángulo <math>\theta</math>. ¿Qué trayectoria sigue el C.I.R. <math>I_{21}</math>, observada desde el sólido &ldquo;1&rdquo;?
		+	# Determine las direcciones tangente y normal a la trayectoria seguida por el punto <math>I_{21}</math>. Calcule las componentes intrínsecas de la velocidad y la aceleración de una partícula que, a lo largo del tiempo, fuese ocupando las sucesivas posiciones del <math>I_{21}</math>.
		+
		+	[[Categoría:Problemas de examen F1 GIA]]

---

última version al 18:34 8 ene 2013

1 Cuestión sobre teoremas de conservación

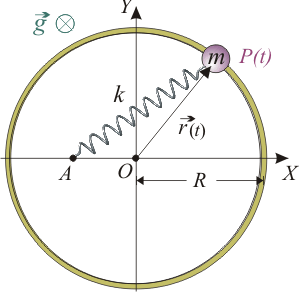
Una pequeña bolita P, de masa m, está insertada en un aro de centro O y radio R, fijado en el plano horizontal OXY. La partícula está sometida a la acción de la gravedad (en la dirección perpendicular al plano,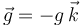 ) y a la de un resorte ideal de longitud natural nula y constante recuperadora k, que tiene un extremo fijo en el punto de circunferencia de coordenadas A( − R / 2,0,0). El rozamiento entre la bolita y el aro es despreciable. Para el sistema descrito, responda razonadamente a las siguientes cuestiones:

1. ¿Se conserva la energía mecánica?
2. ¿Se conserva el momento cinético respecto del punto O?
3. ¿Se conserva el momento cinético respecto del punto A?

2 Partícula en tubo con resortes

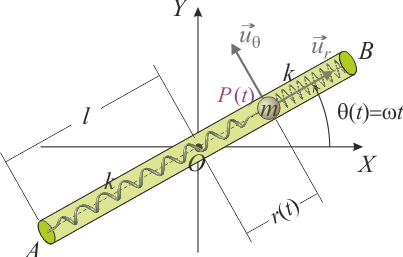
Un tubo estrecho AB de longitud 2l y de masa despreciable, contenido en todo instante en el plano horizontal fijo OXY, gira con velocidad angular constante alrededor de su centro O, de manera que el ángulo que forma el tubo con la dirección OX verifica la ley horaria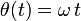 . En el interior del tubo hay una partícula P de masa m, que puede moverse sin rozamiento apreciable. Sendos resortes ideales, ambos de longitud natural nula y constante recuperadora de valor k, conectan la partícula con los extremos A y B del tubo.

1. Escriba las expresiones de los vectores posición, velocidad y aceleración de la partícula en función de la variable r y sus derivadas, utilizando la base de las coordenadas polares 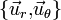. Exprese también las distintas fuerzas que actúan sobre la partícula.
2. Aplique las leyes de la Dinámica para formular las ecuaciones de movimiento del sistema. A la vista de la ecuación diferencial que describe el comportamiento de r(t), indique el tipo de movimiento que realiza la partícula a lo largo del tubo para los siguientes casos: (a) 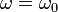; (b) 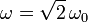, y (c) 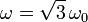, siendo .
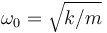3. Considérese la situación particular en que el valor de la velocidad angular es 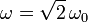-caso (b)-, y en el instante inicial (t = 0) la partícula se halla en el punto O con una velocidad cuyo módulo vale v₀. Obtenga la ley horaria para la variable r(t), así como la fuerza de reacción vincular que actúa sobre la partícula.
4. Obtenga la expresión horaria E(t) para la energía mecánica de la partícula ¿Se conserva E(t)? ¿Por qué?

3 Barra inscrita en un triángulo

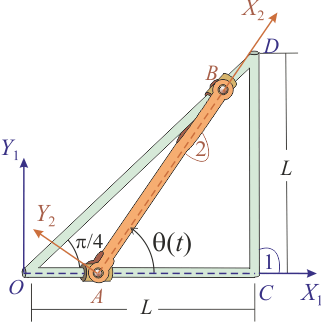
Los extremos A y B de una barra de longitud L (sólido “2”), están obligados a moverse por sendos lados desiguales de un triángulo rectángulo isósceles (sólido “1”). Partiendo del punto O, el extremo A se desliza por el lado OC, también de longitud L, con velocidad constante de módulo v₀. El extremo B se desliza por el lado OD de longitud 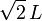. Para indicar la posición de la barra en el sistema se sugiere utilizar el ángulo θ mostrado en la figura.

1. Determine la posición del C.I.R. (punto I₂₁) y una reducción cinemática del movimiento {21}, en función del valor del ángulo θ.
2. Obtenga las derivadas con respecto al tiempo de los vectores de la reducción. Calcule la velocidad y la aceleración instantánea del extremo B en las posiciones inicial y final (extremo A en los puntos O y C, respectivamente).
3. Obtenga la expresión paramétrica de la trayectoria seguida por I₂₁ y la distancia entre este punto y O, en función del valor del ángulo θ. ¿Qué trayectoria sigue el C.I.R. I₂₁, observada desde el sólido “1”?
4. Determine las direcciones tangente y normal a la trayectoria seguida por el punto I₂₁. Calcule las componentes intrínsecas de la velocidad y la aceleración de una partícula que, a lo largo del tiempo, fuese ocupando las sucesivas posiciones del I₂₁.