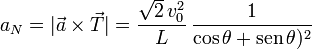Ejercicio de cinemática del sólido,Primera Convocatoria Ordinaria Enero 2012

De Laplace

Contenido

1 Enunciado
2 Solución

1 Enunciado

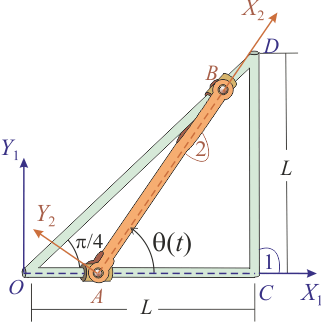
Los extremos $A$ y $B$ de una barra de longitud $L$ (sólido “2”), están obligados a moverse por sendos lados desiguales de un triángulo rectángulo isósceles (sólido “1”). Partiendo del punto $O$ , el extremo $A$ se desliza por el lado $O C$ , también de longitud $L$ , con velocidad constante de módulo $v 0$ . El extremo $B$ se desliza por el lado $O D$ de longitud 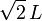$\sqrt{2}\!\ L$ . Para indicar la posición de la barra en el sistema se sugiere utilizar el ángulo $θ$ mostrado en la figura.

Determine la posición del C.I.R. (punto $I 21$ ) y una reducción cinemática del movimiento {21}, en función del valor del ángulo $θ$ .
Obtenga las derivadas con respecto al tiempo de los vectores de la reducción. Calcule la velocidad y la aceleración instantánea del extremo $B$ en las posiciones inicial y final (extremo $A$ en los puntos $O$ y $C$ , respectivamente).
Obtenga la expresión paramétrica de la trayectoria seguida por $I 21$ y la distancia entre este punto y $O$ , en función del valor del ángulo $θ$ . ¿Qué trayectoria sigue el C.I.R. $I 21$ , observada desde el sólido “1”?
Determine las direcciones tangente y normal a la trayectoria seguida por el punto $I 21$ . Calcule las componentes intrínsecas de la velocidad y la aceleración de una partícula que, a lo largo del tiempo, fuese ocupando las sucesivas posiciones del $I 21$ .

2 Solución

2.1 Reducción cinemática

El punto A de la barra (sólido "2") se mueve respecto al triángulo (sólido "1") con velocidad constante a lo largo del eje $O X 1$ . Por tanto

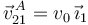
$\vec{v}^{\, A}_{21} = v_0\,\vec{\imath}_1$

Al ser un movimiento plano, el vector rotación $\vec{\omega}_{21}$ es perpendicular al plano del dibujo. Como el eje $O Z$ apunta hacia fuera tenemos

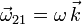
$\vec{\omega}_{21} = \omega\,\vec{k}$

Si escogemos un eje $O X 2$ que coincida con la barra y se mueva solidariamente con ella, el ángulo que forma con el eje $O X 1$ es $θ(t)$ . Por tanto la componente de $\vec{\omega}_{21}$ es precisamente la derivada temporal de este ángulo. Por tanto, la reducción cinemática del movimiento {21} en el punto A está compuesta por los vectores

$\vec{v}^{\,A}_{21} = v_0\,\vec{\imath}_1\quad\quad\vec{\omega}_{21} =\dot{\theta}\,\vec{k}_1$

Nos falta encontrar una expresión para $\dot{\theta}$ . Esto puede hacerse de varias maneras. Vamos a mostrar cuatro formas diferentes de hacerlo.

2.1.1 Usando la dirección de la velocidad 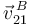$\vec{v}^{\,B}_{21}$

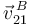Conocemos la dirección del vector rotación $\vec{\omega}_{21}$ , la velocidad en un punto $\vec{v}^{\,A}_{21}$ y la dirección de la velocidad $\vec{v}^{\,B}_{21}$ (el punto B esta obligado a moverse sobre la recta OD). Esta es información suficiente para calcular la componente del vector rotación.

Usando el teorema de Chasles, relacionamos las velocidades en los puntos A y B

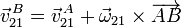
$\vec{v}^{\,B}_{21} = \vec{v}^{\,A}_{21} + \vec{\omega}_{21}\times\overrightarrow{AB}$

Del dibujo obtenemos el vector geométrico 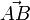$\vec{AB}$

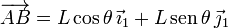
$\overrightarrow{AB} = L\cos\theta\,\vec{\imath}_1 + L\,\mathrm{sen}\,\theta\,\vec{\jmath}_1$

El producto vectorial es

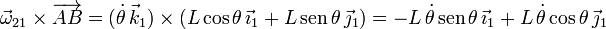
$\vec{\omega}_{21}\times\overrightarrow{AB} = (\dot{\theta}\,\vec{k}_1) \times(L\cos\theta\,\vec{\imath}_1 + L\,\mathrm{sen}\,\theta\,\vec{\jmath}_1)= -L\,\dot{\theta}\,\mathrm{sen}\,\theta\,\vec{\imath}_1 +L\,\dot{\theta}\cos\theta\,\vec{\jmath}_1$

Por tanto la velocidad del punto B en el movimiento {21} es

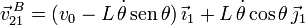
$\vec{v}^{\,B}_{21} = (v_0-L\,\dot{\theta}\,\mathrm{sen}\,\theta)\,\vec{\imath}_1 + L\,\dot{\theta}\cos\theta\,\vec{\jmath}_1$

El punto B está obligado a moverse sobre la recta OD. Como esta recta forma un ángulo $π / 4$ con el eje $O X 1$ , un vector paralelo a esta recta es

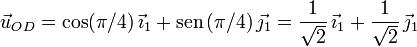
$\vec{u}_{OD} = \cos(\pi/4)\,\vec{\imath}_1 + \mathrm{sen}\, (\pi/4)\,\vec{\jmath_1} = \dfrac{1}{\sqrt{2}}\,\vec{\imath}_1 + \dfrac{1}{\sqrt{2}}\,\vec{\jmath}_1$

La velocidad 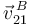$\vec{v}^{\,B}_{21}$ debe ser paralela a $\vec{u}_{OD}$ , por lo que

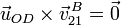
$\vec{u}_{OD}\times\vec{v}^{\,B}_{21}=\vec{0}$

El producto vectorial es

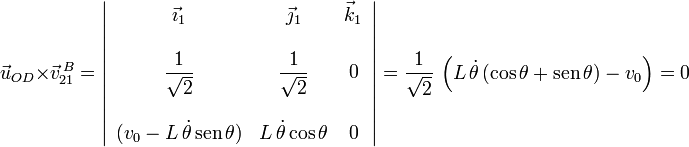
$\vec{u}_{OD}\times\vec{v}^{\,B}_{21}= \left| \begin{array}{ccc} \vec{\imath}_1 & \vec{\jmath}_1 & \vec{k}_1\\ &&\\ \dfrac{1}{\sqrt{2}}&\dfrac{1}{\sqrt{2}}&0\\ &&\\ (v_0-L\,\dot{\theta}\,\mathrm{sen}\,\theta)&L\,\dot{\theta}\cos\theta&0 \end{array} \right|= \dfrac{1}{\sqrt{2}}\,\left( L\,\dot{\theta}\,(\cos\theta+\mathrm{sen}\,\theta) - v_0 \right) = 0$

Despejando $\dot{\theta}$ obtenemos

$\dot{\theta} = \dfrac{v_0}{L}\,\dfrac{1}{\mathrm{sen}\,\theta+\cos\theta}$

La expresión final de la reducción cinemática del movimiento {21} es

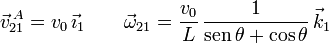
$\vec{v}^{\,A}_{21} = v_0\,\vec{\imath}_1\quad\quad \vec{\omega}_{21} = \dfrac{v_0}{L}\,\dfrac{1}{\mathrm{sen}\,\theta+\cos\theta}\,\vec{k}_1$

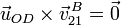
Otra forma de llegar a este resultado es multiplicar vectorialmente por $\vec{u}_{OD}$ en la expresión del teorema de Chasles, y usar que $\vec{u}_{OD}\times\vec{v}^{\,B}_{21}=\vec{0}$

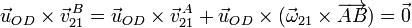
$\vec{u}_{OD}\times\vec{v}^{\,B}_{21} = \vec{u}_{OD}\times\vec{v}^{\,A}_{21} + \vec{u}_{OD}\times(\vec{\omega}_{21}\times\overrightarrow{AB}) =\vec{0}$

Desarrollando el doble producto vectorial

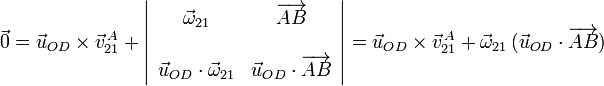
$\vec{0} = \vec{u}_{OD}\times\vec{v}^{\,A}_{21} + \left| \begin{array}{cc} \vec{\omega}_{21}&\overrightarrow{AB}\\ &\\ \vec{u}_{OD}\cdot\vec{\omega}_{21} & \vec{u}_{OD}\cdot\overrightarrow{AB} \end{array} \right| = \vec{u}_{OD}\times\vec{v}^{\,A}_{21} + \vec{\omega}_{21}\,(\vec{u}_{OD}\cdot\overrightarrow{AB})$

Hemos usado que 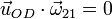$\vec{u}_{OD}\cdot\vec{\omega}_{21}=0$ , pues son vectores perpendiculares. Como $\vec{\omega}_{21}$ está multiplicado por un escalar, podemos despejar el vector, para obtener

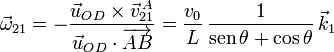
$\vec{\omega}_{21} = -\dfrac{\vec{u}_{OD}\times\vec{v}^{\,A}_{21}}{\vec{u}_{OD}\cdot\overrightarrow{AB}} = \dfrac{v_0}{L}\,\dfrac{1}{\mathrm{sen}\,\theta+\cos\theta}\,\vec{k}_1$

2.1.2 A partir del CIR del movimiento {21}

El CIR del movimiento {21}, $I 21$ puede determinarse gráficamente. Para ello, trazamos por los puntos A y B las perpendiculares a sus velocidades respectivas. El punto de corte es $I 21$ . Como puede observase en el dibujo, el vector 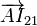$\overrightarrow{AI}_{21}$ puede expresarse como

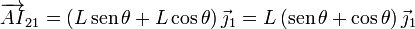
$\overrightarrow{AI}_{21} = (L\,\mathrm{sen}\,\theta + L\cos\theta)\,\vec{\jmath}_1 = L\,(\mathrm{sen}\,\theta + \cos\theta)\,\vec{\jmath}_1$

Ahora usamos el teorema de Chasles para relacionar las velocidades en A y $I 21$

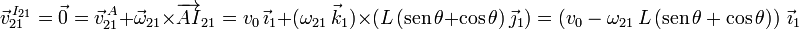
$\vec{v}^{\,I_{21}}_{21} = \vec{0}=\vec{v}^{\,A}_{21} + \vec{\omega}_{21}\times\overrightarrow{AI}_{21} = v_0\,\vec{\imath}_1 + (\omega_{21}\,\vec{k}_{1})\times(L\,(\mathrm{sen}\,\theta + \cos\theta)\,\vec{\jmath}_1) = \left( v_0 - \omega_{21}\,L\,(\mathrm{sen}\,\theta + \cos\theta) \right)\,\vec{\imath}_1$

De aquí obtenemos

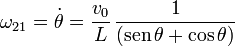
$\omega_{21}=\dot{\theta} = \dfrac{v_0}{L}\,\dfrac{1}{(\mathrm{sen}\,\theta + \cos\theta)}$

2.1.3 A partir de la geometría del triángulo

Otra forma de obtener la derivada del ángulo es usando la geometría del problema. Del dibujo observamos que

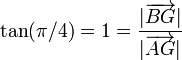
$\tan(\pi/4) = 1 = \dfrac{|\overrightarrow{BG}|}{|\overrightarrow{AG}|}$

Tenemos que

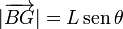
$|\overrightarrow{BG}| = L\,\mathrm{sen}\,\theta$

y

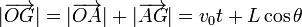
$|\overrightarrow{OG}| = |\overrightarrow{OA}| + |\overrightarrow{AG}| = v_0t + L\cos\theta$

Sustituyendo arriba obtenemos

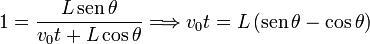
$1 = \dfrac{ L\,\mathrm{sen}\,\theta}{v_0t + L\cos\theta} \Longrightarrow v_0t = L\,(\mathrm{sen}\,\theta - \cos\theta)$

Derivando respecto al tiempo en ambos lados de la igualdad tenemos

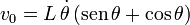
$v_0 = L\,\dot{\theta}\,(\mathrm{sen}\,\theta + \cos\theta)$

de donde reobtenemos los resultados anteriores.

2.1.4 Usando el teorema del seno

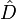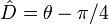La relación entre el ángulo y el tiempo del apartado anterior puede obtenerse también usando el teorema del seno en el triángulo OCD. Vemos en el dibujo que el ángulo $\hat{D}$ es $\hat{D}=\theta-\pi/4$ . Usamos el teorema del seno para relacionar los lados 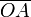$\overline{OA}$ y $\overline{AB}$

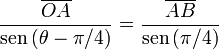
$\dfrac{\overline{OA}}{\mathrm{sen}\,(\theta-\pi/4)} = \dfrac{\overline{AB}}{\mathrm{sen}\,(\pi/4)}$

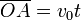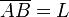Sabemos que $\overline{OA} = v_0t$ y $\overline{AB}=L$ , por lo que despejando obtenemos

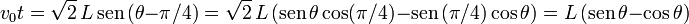
$v_0t = \sqrt{2}\,L\,\mathrm{sen}\,(\theta-\pi/4) = \sqrt{2}\,L\,(\mathrm{sen}\,\theta\cos(\pi/4) - \mathrm{sen}\,(\pi/4) \cos\theta) = L\,(\mathrm{sen}\,\theta - \cos\theta)$

Derivando en ambos lados obtenemos la expresión de $\dot{\theta}$

2.1.5 Posición del CIR

El CIR puede determinarse geométricamente o, una vez que se tiene la reducción, usando la fórmula analítica

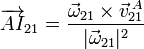
$\overrightarrow{AI}_{21} = \dfrac{\vec{\omega}_{21}\times\vec{v}^{\,A}_{21}}{|\vec{\omega}_{21}|^2}$

Esta expresión nos da el vector que va desde el punto A hasta el CIR. Haciendo los cálculos tenemos

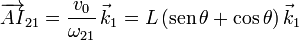
$\overrightarrow{AI}_{21} = \dfrac{v_0}{\omega_{21}}\,\vec{k}_1 = L\,(\mathrm{sen}\,\theta + \cos{\theta})\,\vec{k}_1$

La posición del centro de masas desde el origen es

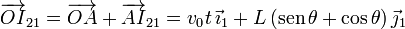
$\overrightarrow{OI}_{21} = \overrightarrow{OA} + \overrightarrow{AI}_{21} = v_0t\,\vec{\imath}_1 + L\,(\mathrm{sen}\,\theta + \cos\theta)\,\vec{\jmath}_1$

2.2 Derivada de la reducción cinemática y velocidades y aceleración del punto B

La velocidad del punto es constante en el tiempo vista desde el sólido "1". Su aceleración es

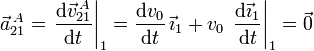
$\vec{a}^{\,A}_{21} = \left.\dfrac{\mathrm{d}\vec{v}^{\,A}_{21}}{\mathrm{d}t}\right|_{1} = \dfrac{\mathrm{d}v_0}{\mathrm{d}t}\,\vec{\imath}_{1} + v_0\,\left.\dfrac{\mathrm{d}\vec{\imath}_{1}}{\mathrm{d}t}\right|_{1} = \vec{0}$

Ambas derivadas son nulas.

Para la aceleración angular tenemos

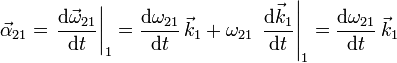
$\vec{\alpha}_{21} = \left.\dfrac{\mathrm{d}\vec{\omega}_{21}}{\mathrm{d}t}\right|_1 = \dfrac{\mathrm{d}\omega_{21}}{\mathrm{d}t}\,\vec{k}_1 + \omega_{21}\,\left.\dfrac{\mathrm{d}\vec{k}_1}{\mathrm{d}t}\right|_1 =\dfrac{\mathrm{d}\omega_{21}}{\mathrm{d}t}\,\vec{k}_1$

Para hacer esta derivada usamos la regla de la cadena

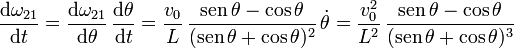
$\dfrac{\mathrm{d}\omega_{21}}{\mathrm{d}t} = \dfrac{\mathrm{d}\omega_{21}}{\mathrm{d}\theta}\,\dfrac{\mathrm{d}\theta}{\mathrm{d}t} = \dfrac{v_0}{L}\,\dfrac{\mathrm{sen}\,\theta-\cos\theta}{(\mathrm{sen}\,\theta+ \cos\theta)^2}\,\dot{\theta}= \dfrac{v_0^2}{L^2}\,\dfrac{\mathrm{sen}\,\theta-\cos\theta}{(\mathrm{sen}\,\theta+ \cos\theta)^3}$

Así pues, la derivada temporal de la reducción cinemática en el punto A es

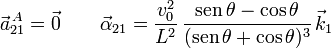
$\vec{a}^{\,A}_{21} = \vec{0} \quad\quad \vec{\alpha}_{21} = \dfrac{v_0^2}{L^2}\,\dfrac{\mathrm{sen}\,\theta-\cos\theta}{(\mathrm{sen}\,\theta+ \cos\theta)^3}\,\vec{k}_1$

2.2.1 Velocidad y aceleración en B en los instantes inicial y final

Dada la reducción cinemática y su derivada en A, podemos obtener la velocidad y la aceleración en el punto B usando el teorema de Chasles y la ecuación del campo de aceleraciones

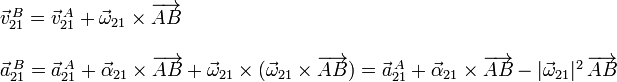
$\begin{array}{l} \vec{v}^{\,B}_{21} = \vec{v}^{\,A}_{21} + \vec{\omega}_{21}\times\overrightarrow{AB}\\ \\ \vec{a}^{\,B}_{21} = \vec{a}^{\,A}_{21} + \vec{\alpha}_{21}\times\overrightarrow{AB} +\vec{\omega}_{21}\times(\vec{\omega}_{21}\times\overrightarrow{AB}) = \vec{a}^{\,A}_{21} + \vec{\alpha}_{21}\times\overrightarrow{AB} -|\vec{\omega}_{21}|^2\,\overrightarrow{AB} \end{array}$

Hemos usado que es un movimiento plano para simplificar la ecuación del campo de aceleraciones.

En el instante inicial el punto A está sobre el punto O, por lo que el ángulo es $θ(t = 0) = π / 4$ . En este instante los vectores implicados valen

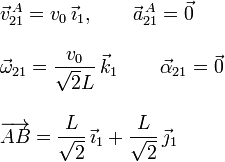
$\begin{array}{l} \vec{v}^{\,A}_{21} = v_0\,\vec{\imath}_1, \qquad \vec{a}^{\,A}_{21}=\vec{0}\\ \\ \vec{\omega}_{21} = \dfrac{v_0}{\sqrt{2}L}\,\vec{k}_1\,\qquad \vec{\alpha}_{21} = \vec{0}\\ \\ \overrightarrow{AB} = \dfrac{L}{\sqrt{2}}\,\vec{\imath}_1 + \dfrac{L}{\sqrt{2}}\,\vec{\jmath}_1 \end{array}$

Calculando las operaciones obtenemos

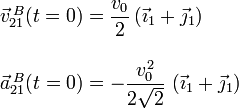
$\begin{array}{l} \vec{v}^{\,B}_{21} ( t=0 ) = \dfrac{v_0}{2}\,(\vec{\imath}_1 + \vec{\jmath}_1) \\ \\ \vec{a}^{\,B}_{21} ( t=0 ) = -\dfrac{v_0^2}{2\sqrt{2}}\,\left(\vec{\imath}_1 + \vec{\jmath}_1\right) \end{array}$

En el instante final $t f$ , el punto A coincide con el punto C, y el valor del ángulo es $θ(t f) = π / 2$ . Los vectores relevantes son

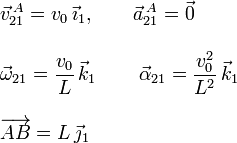
$\begin{array}{l} \vec{v}^{\,A}_{21} = v_0\,\vec{\imath}_1, \qquad \vec{a}^{\,A}_{21}=\vec{0}\\ \\ \vec{\omega}_{21} = \dfrac{v_0}{L}\,\vec{k}_1\,\qquad \vec{\alpha}_{21} = \dfrac{v_0^2}{L^2}\,\vec{k}_1\\ \\ \overrightarrow{AB} = L\,\vec{\jmath}_1 \end{array}$

Calculando las operaciones obtenemos

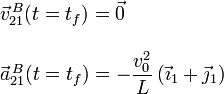
$\begin{array}{l} \vec{v}^{\,B}_{21} ( t=t_f ) = \vec{0} \\ \\ \vec{a}^{\,B}_{21} ( t=t_f ) = -\dfrac{v_0^2}{L}\,(\vec{\imath}_1 + \vec{\jmath}_1) \end{array}$

2.3 Ecuaciones paramétricas del CIR

En el primer apartado hemos obtenido la posición del CIR respecto al punto O

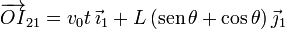
$\overrightarrow{OI}_{21} = v_0t\,\vec{\imath}_1 + L\,(\mathrm{sen}\,\theta + \cos\theta)\,\vec{\jmath}_1$

Queremos expresar este vector en términos del parámetro $θ$ . Para ello usamos la relación entre el tiempo y el ángulo que obtuvimos al aplicar el teorema del seno, (o bien al analizar la geometría del sistema)

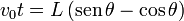
$v_0t = L\,(\mathrm{sen}\,\theta - \cos\theta)$

De este modo las ecuaciones paramétricas quedan

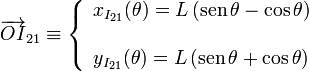
$\overrightarrow{OI}_{21} \equiv \left\{ \begin{array}{l} x_{I_{21}}(\theta) = L\,(\mathrm{sen}\,\theta - \cos\theta) \\ \\ y_{I_{21}}(\theta) = L\,(\mathrm{sen}\,\theta + \cos\theta) \end{array} \right.$

La distancia al punto O es el módulo de ese vector

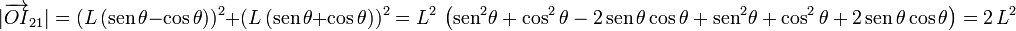
$|\overrightarrow{OI}_{21}| = (L\,(\mathrm{sen}\,\theta - \cos\theta))^2+ (L\,(\mathrm{sen}\,\theta + \cos\theta))^2 =L^2\,\left(\mathrm{sen}^2\theta + \cos^2\theta - 2\,\mathrm{sen}\,\theta\cos\theta + \mathrm{sen}^2\theta + \cos^2\theta + 2\,\mathrm{sen}\,\theta\cos\theta\right) = 2\,L^2$

La distancia de $I 21$ al punto O es constante, y se mueve siempre en el plano $O X 1 Y 1$ . Por tanto, la trayectoria que describe el CIR es una circunferencia de radio 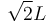$\sqrt{2}L$ con centro en el punto O.

2.4 Componentes intrínsecas de una partícula que se mueva como el CIR

El vector de posición de una partícula que se mueva como el CIR es

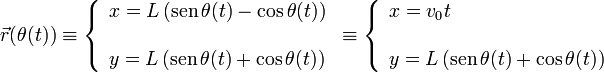
$\vec{r}(\theta(t)) \equiv \left\{ \begin{array}{l} x = L\,(\mathrm{sen}\,\theta(t) - \cos\theta(t)) \\ \\ y = L\,(\mathrm{sen}\,\theta(t) + \cos\theta(t)) \end{array} \right. \equiv \left\{ \begin{array}{l} x = v_0 t \\ \\ y = L\,(\mathrm{sen}\,\theta(t) + \cos\theta(t)) \end{array} \right.$

Es mas sencillo usar la segunda expresión para calcular la velocidad y la aceleración. Para calcular la velocidad derivamos respecto al tiempo las dos componentes

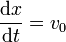
$\dfrac{\mathrm{d}x}{\mathrm{d}t} = v_0$

y

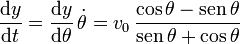
$\dfrac{\mathrm{d}y}{\mathrm{d}t} = \dfrac{\mathrm{d}y}{\mathrm{d}\theta}\,\dot{\theta} = v_0\,\dfrac{\cos\theta-\mathrm{sen}\,\theta}{\mathrm{sen}\,\theta + \cos\theta}$

Con lo que la velocidad es

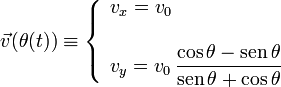
$\vec{v}(\theta(t)) \equiv \left\{ \begin{array}{l} v_x = v_0 \\ \\ v_y = v_0\,\dfrac{\cos\theta-\mathrm{sen}\,\theta}{\mathrm{sen}\,\theta + \cos\theta} \end{array} \right.$

El módulo de la velocidad es

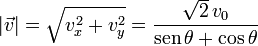
$|\vec{v}| = \sqrt{v_x^2+v_y^2} = \dfrac{\sqrt{2}\,v_0}{\mathrm{sen}\,\theta+\cos\theta}$

La aceleración la obtenemos derivando el vector velocidad

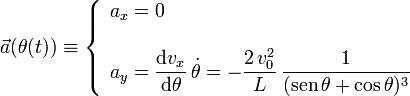
$\vec{a}(\theta(t)) \equiv \left\{ \begin{array}{l} a_x = 0 \\ \\ a_y = \dfrac{\mathrm{d}v_x}{\mathrm{d}\theta}\,\dot{\theta} = -\dfrac{2\,v_0^2}{L}\,\dfrac{1}{(\mathrm{sen}\,\theta+\cos\theta)^3} \end{array} \right.$

Podemos obtener el vector tangente a partir de la velocidad

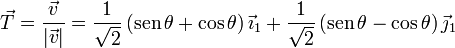
$\vec{T} = \dfrac{\vec{v}}{|\vec{v}|} = \dfrac{1}{\sqrt{2}}\,(\mathrm{sen}\,\theta + \cos\theta)\,\vec{\imath}_1 + \dfrac{1}{\sqrt{2}}\,(\mathrm{sen}\,\theta-\cos\theta)\,\vec{\jmath}_1$

La componente intrínseca de la velocidad es

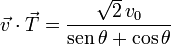
$\vec{v}\cdot\vec{T} = \dfrac{\sqrt{2}\,v_0}{\mathrm{sen}\,\theta + \cos\theta}$

La aceleración tangencial es

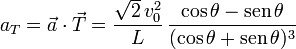
$a_T = \vec{a}\cdot\vec{T} = \dfrac{\sqrt{2}\,v_0^2}{L}\,\dfrac{\cos\theta - \mathrm{sen}\,\theta}{(\cos\theta+\mathrm{sen}\,\theta)^3}$

y la aceleración normal es

$a_N = |\vec{a}\times\vec{T}| = \dfrac{\sqrt{2}\,v_0^2}{L}\,\dfrac{1}{\cos\theta+\mathrm{sen}\,\theta)^2}$

Ejercicio de cinemática del sólido,Primera Convocatoria Ordinaria Enero 2012

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Reducción cinemática

2.1.1 Usando la dirección de la velocidad $\vec{v}^{\,B}_{21}$

2.1.2 A partir del CIR del movimiento {21}

2.1.3 A partir de la geometría del triángulo

2.1.4 Usando el teorema del seno

2.1.5 Posición del CIR

2.2 Derivada de la reducción cinemática y velocidades y aceleración del punto B

2.2.1 Velocidad y aceleración en B en los instantes inicial y final

2.3 Ecuaciones paramétricas del CIR

2.4 Componentes intrínsecas de una partícula que se mueva como el CIR

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES