Fuerza entre dos hilos cargados

De Laplace

(Diferencias entre revisiones)

Revisión de 15:59 4 nov 2008

Contenido

1 Enunciado
2 Solución

1 Enunciado

Un cable formado por dos hilos paralelos produce un campo eléctrico similar al producido por dos líneas infinitas con densidad de carga $λ$ y $- λ$ , situadas a una distancia $D$ una de la otra.

Se trata de hallar la fuerza por unidad de longitud con que se atraen los dos hilos. Para ello, calcule:

El campo eléctrico en cualquier punto del espacio, creado por un segmento rectilíneo de longitud $L$ , sobre el cual existe una densidad de carga uniforme $λ$ .
A partir del resultado anterior, halle el campo en cualquier punto debido a una línea de carga uniforme infinitamente larga.
Halle la fuerza que uno de los hilos produce sobre un segmento de longitud $h$ del otro hilo.

2 Solución

2.1 Campo de un segmento cargado

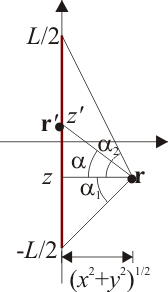
Sin pérdida de generalidad, podemos colocar el eje $z$ sobre el segmento y el origen de coordenadas en su punto medio.

La expresión integral para el campo eléctrico debido a una distribución de carga lineal se expresa

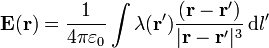
$\mathbf{E}(\mathbf{r})=\frac{1}{4\pi\varepsilon_0} \int\lambda(\mathbf{r}')\frac{(\mathbf{r}-\mathbf{r}')}{|\mathbf{r}-\mathbf{r}'|^3}\,\mathrm{d}l'$

En nuestro caso, la posición de las fuentes es

$x'=0\quad y'=0\quad z'=z'$ $z'\in\left[-\frac{L}{2},\frac{L}{2}\right]$

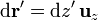
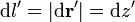
$\mathrm{d}\mathbf{r}'=\mathrm{d}z'\,\mathbf{u}_{z}$ $\mathrm{d}l'=|\mathrm{d}\mathbf{r}'|=\mathrm{d}z'$

por lo que la integral se convierte en

$\mathbf{E}(\mathbf{r})=\frac{1}{4\pi\varepsilon_0} \int_{-L/2}^{L/2} \!\!\lambda \frac{(x\mathbf{u}_{x}+y\mathbf{u}_{y}+(z-z')\mathbf{u}_{z})} {\left(x^2+y^2+(z-z')^2\right)^{3/2}}\,\mathrm{d}z'$

Separando componente a componente

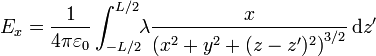
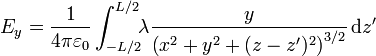
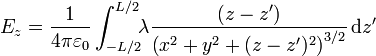
$E_x= \frac{1}{4\pi\varepsilon_0} \int_{-L/2}^{L/2}\!\!\lambda \frac{ x} {\left(x^2+y^2+(z-z')^2\right)^{3/2}}\,\mathrm{d}z'$ $E_y= \frac{1}{4\pi\varepsilon_0} \int_{-L/2}^{L/2}\!\!\lambda \frac{y} {\left(x^2+y^2+(z-z')^2\right)^{3/2}}\,\mathrm{d}z'$ $E_z= \frac{1}{4\pi\varepsilon_0} \int_{-L/2}^{L/2}\!\!\lambda \frac{ (z-z')} {\left(x^2+y^2+(z-z')^2\right)^{3/2}}\,\mathrm{d}z'$

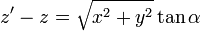
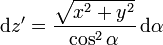
Podemos llevar a cabo estas integrales mediante el cambio de variable $z'-z=\sqrt{x^2+y^2}\tan\alpha$ $\mathrm{d}z'=\frac{\sqrt{x^2+y^2}}{\cos^2\alpha}\,\mathrm{d}\alpha$

Este ángulo posee interpretación geométrica ya que es el que forma la dirección al punto donde está la fuente con la horizontal.

Con este cambio las integrales quedan

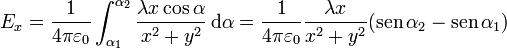
$E_x= \frac{1}{4\pi\varepsilon_0} \int_{\alpha_1}^{\alpha_2}\frac{\lambda x\cos\alpha} {x^2+y^2}\,\mathrm{d}\alpha=\frac{1}{4\pi\varepsilon_0} \frac{\lambda x}{x^2+y^2}(\mathrm{sen}\,\alpha_2-\mathrm{sen}\,\alpha_1)$ $E_y= \frac{1}{4\pi\varepsilon_0} \int_{\alpha_1}^{\alpha_2}\frac{\lambda y\cos\alpha} {x^2+y^2}\,\mathrm{d}\alpha=\frac{1}{4\pi\varepsilon_0} \frac{\lambda y}{x^2+y^2}(\mathrm{sen}\,\alpha_2-\mathrm{sen}\,\alpha_1)$ $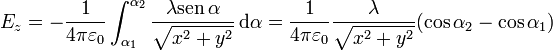E_z= -\frac{1}{4\pi\varepsilon_0} \int_{\alpha_1}^{\alpha_2}\frac{\lambda \mathrm{sen}\,\alpha} {\sqrt{x^2+y^2}}\,\mathrm{d}\alpha= \frac{1}{4\pi\varepsilon_0} \frac{\lambda }{\sqrt{x^2+y^2}}(\cos\alpha_2-\cos\alpha_1)$

Los senos y cosenos que aparecen en las expresiones anteriores corresponden a los valores límite de $α$ y su relación con las coordenadas cartesianas es

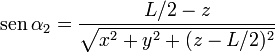
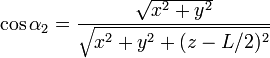
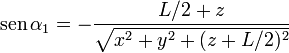
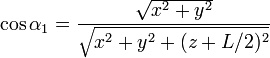
$\mathrm{sen}\,\alpha_2=\frac{L/2-z}{\sqrt{x^2+y^2+(z-L/2)^2}}$ $\cos\alpha_2=\frac{\sqrt{x^2+y^2}}{\sqrt{x^2+y^2+(z-L/2)^2}}$ $\mathrm{sen}\,\alpha_1=-\frac{L/2+z}{\sqrt{x^2+y^2+(z+L/2)^2}}$ $\cos\alpha_1=\frac{\sqrt{x^2+y^2}}{\sqrt{x^2+y^2+(z+L/2)^2}}$

Agrupando los resultados tenemos la forma vectorial

$\mathbf{E}=\frac{\lambda}{4\pi\varepsilon}\left(\frac{x\mathbf{u}_{x}+y\mathbf{u}_{y}}{x^2+y^2} \left(\mathrm{sen}\,\alpha_2-\mathrm{sen}\,\alpha_1\right)+ \frac{\mathbf{u}_{z}(\cos\alpha_2-\cos\alpha_1)}{\sqrt{x^2+y^2}}\right)$

Si expresamos el campo en coordenadas cilíndricas centradas en el hilo nos queda

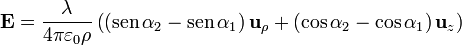
$\mathbf{E}=\frac{\lambda}{4\pi\varepsilon_0\rho} \left(\left(\mathrm{sen}\,\alpha_2-\mathrm{sen}\,\alpha_1\right)\mathbf{u}_{\rho}+ \left(\cos\alpha_2-\cos\alpha_1\right)\mathbf{u}_{z}\right)$

que podemos leer como el campo posee una componente en la dirección radial perpendicular al eje del segmento y una componente paralela a él. Esta interpretación nos seguirá valiendo cuando el eje $z$ no esté situado sobre el segmento.

Para ello consideraremos un segmento $A B$ y un punto de observación arbitrario $P$ . Trazamos la recta perpendicular a $A B$ por $P$ . Esta recta cortará a la primera en un punto $C$ . La variable $ρ$ será la longitud del segmento $P C$ . El ángulo $α 1$ será el que forma esta perpendicular con el segmento $P A$ y el $α 2$ con el segmento $P B$ . Ambos ángulos serán positivos si la perpendicular queda por detrás del segmento (considerando adelante aquél en que apunta $\mathbf{u}_z$ ) y negativos en caso contrario. Si la perpendicular incide sobre el segmento $A B$ , el ángulo $α 2$ será positivo y el $α 1$ negativo.

Un límite interesante de la expresión anterior es aquel en que 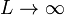$L\to\infty$ , entonces, cualquiera que sea el punto de observación, 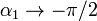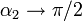$\alpha_1\to -\pi/2$ , $\alpha_2\to \pi/2$ , por lo que

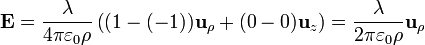
$\mathbf{E}=\frac{\lambda}{4\pi\varepsilon_0\rho}\left((1-(-1))\mathbf{u}_{\rho}+(0-0)\mathbf{u}_{z}\right)= \frac{\lambda}{2\pi\varepsilon_0\rho}\mathbf{u}_{\rho}$

Este resultado se obtiene, empleando la ley de Gauss, en otro problema.

2.2 Campo de un hilo infinito

2.3 Fuerza entre los hilos

@@ Línea 45: / Línea 45: @@
 </math></center>
-[[Imagen:segmentocargado.gif|left]]Podemos llevar a cabo estas integrales mediante el cambio de variable
+[[Imagen:segmentocargado.png|left]]Podemos llevar a cabo estas integrales mediante el cambio de variable
 <center><math>z'-z=\sqrt{x^2+y^2}\tan\alpha</math>{{qquad}}{{qquad}}

Fuerza entre dos hilos cargados

De Laplace

Revisión de 15:59 4 nov 2008

Contenido

1 Enunciado

2 Solución

2.1 Campo de un segmento cargado

2.2 Campo de un hilo infinito

2.3 Fuerza entre los hilos

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES