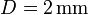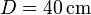Campo eléctrico entre dos varillas

De Laplace

(Diferencias entre revisiones)

Revisión de 13:40 30 oct 2008

Contenido

1 Enunciado
2 Solución

1 Enunciado

Dos varillas rectilíneas de longitud $L$ están situadas paralelamente a una distancia $D$ . Las varillas poseen cargas 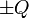$\pm Q$ distribuidas uniformemente.

Halle aproximadamente el campo eléctrico en un punto $P$ equidistante de ambas varillas, para el caso $D\gg L$ .
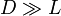Calcule, también de forma aproximada, el valor del campo en el mismo punto $P$ , para el caso $D\ll L$ .
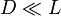Calcule el valor exacto del campo eléctrico en dicho punto $P$ , para un valor arbitrario de $D$ .
Compare los valores exactos y aproximados para el caso 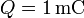, , 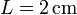y
1. $D=2\,\mathrm{mm}$
2. $D=40\,\mathrm{cm}$

2 Solución

2.1 Caso de dos varillas muy alejadas

Si la distancia entre las varillas es muy grande, comparada con su tamaño, desde el punto central se apreciará cada una aproximadamente como una carga puntual.

La distancia de $P$ a esas cargas puntuales será, también aproximadamente, $D / 2$ . Los campos debidos a cada carga serán iguales en el punto central y ambos irán de la varilla positiva a la negativa (dirección y sentido de 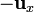$-\mathbf{u}_{x}$ . Por tanto, el campo en $P$ vale aproximadamente

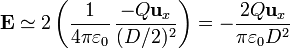
$\mathbf{E} \simeq 2\left(\displaystyle\frac{1}{4\pi\varepsilon_0}\,\frac{-Q\mathbf{u}_{x}}{(D/2)^2}\right) = -\frac{2Q\mathbf{u}_{x}}{\pi\varepsilon_0 D^2}$

Este campo tiende a cero cuando 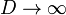$D\to\infty$ , pero no se trata de hallar su valor límite (nulo), sino de estudiar cómo se comporta para distancias grandes.

2.2 Caso de dos varillas muy próximas

Cuando la distancia entre las varillas es muy corta comparada con su longitud, podemos aproximar cada varilla como una línea infinita de carga, con densidad de carga 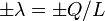$\pm\lambda = \pm Q/L$ .

El campo creado por una línea infinita de carga situada en el eje $z$ puede calcularse bien por integración directa, bien por aplicación de la ley de Gauss (como en otro problema). En cualquier caso, el campo que produce, en cartesianas, es

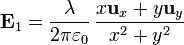
$\mathbf{E}_1 = \frac{\lambda}{2\pi\varepsilon_0}\,\frac{x\mathbf{u}_{x}+y\mathbf{u}_{y}}{x^2+y^2}$

Si la varilla no está en el eje $z$ sino en $x' = D / 2$ , $y' = 0$ el campo es

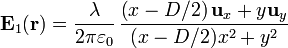
$\mathbf{E}_1(\mathbf{r}) = \frac{\lambda}{2\pi\varepsilon_0}\,\frac{\left(x-D/2\right)\mathbf{u}_{x}+y\mathbf{u}_{y}}{(x-D/2)x^2+y^2}$

El campo debido a esta varilla, en el punto $P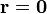$ ( $\mathbf{r}=\mathbf{0}$ ) será, sustituyendo

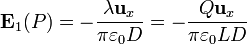
$\mathbf{E}_1(P)= -\frac{\lambda \mathbf{u}_{x}}{\pi\varepsilon_0 D} = -\frac{Q\mathbf{u}_{x}}{\pi\varepsilon_0 L D}$

Éste es el campo debido a la varilla cargada positivamente. El de la cargada negativamente se obtiene del mismo modo, considerando carga opuesta y posición en $x' = - D / 2$ . El resultado es exactamente el mismo, por lo que el campo total es el doble del que crea una sola de las varillas

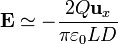
$\mathbf{E}\simeq -\frac{2Q\mathbf{u}_{x}}{\pi\varepsilon_0 L D}$

Este campo tiende a infinito para 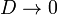$D\to 0$ , pero de nuevo se trata de estudiar su comportamiento, no de hallar su valor límite.

2.3 Caso general

2.4 Comparación con los casos aproximados

@@ Línea 38: / Línea 38: @@
 Éste es el campo debido a la varilla cargada positivamente. El de la cargada negativamente se obtiene del mismo modo, considerando carga
-opuesta y posición en $x'=-D/2$. El resultado es exactamente el mismo, por lo que el campo total es el doble del que crea una sola de las
+opuesta y posición en <math>x'=-D/2</math>. El resultado es exactamente el mismo, por lo que el campo total es el doble del que crea una sola de las varillas
-varillas
 <center><math>\mathbf{E}\simeq -\frac{2Q\mathbf{u}_{x}}{\pi\varepsilon_0 L D}</math></center>

Campo eléctrico entre dos varillas

De Laplace

Revisión de 13:40 30 oct 2008

Contenido

1 Enunciado

2 Solución

2.1 Caso de dos varillas muy alejadas

2.2 Caso de dos varillas muy próximas

2.3 Caso general

2.4 Comparación con los casos aproximados

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES