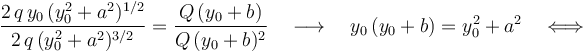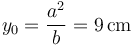Sistema electrostático de tres cargas puntuales

De Laplace

(Diferencias entre revisiones)

Revisión de 12:48 18 sep 2012

1 Enunciado

Un sistema electrostático está formado por tres cargas eléctricas puntuales. Dos de ellas tienen idéntico valor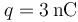 $q=3\,\mathrm{nC}$ y se hallan en los puntos

P 1

y

P 2

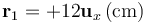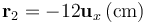, dados por los vectores de posición $\mathbf{r}_1=+12\mathbf{u}_x\,\mathrm{(cm)}$ y $\mathbf{r}_2=-12\mathbf{u}_x\,\mathrm{(cm)}$ , respectivamente. La tercera carga tiene un valor

Q

y se halla en el punto

P 3

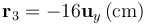, dado por $\mathbf{r}_3=-16\mathbf{u}_y\,\mathrm{(cm)}$ .

Determine, si es posible, el valor que debe tener la carga $Q$ y la posición 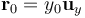$\mathbf{r}_0=y_0\mathbf{u}_y$ de un punto del eje $O Y$ en el cuál se anulen simultáneamente el potencial y el campo eléctrico creado por el sistema de tres cargas.
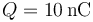¿Cuál es la energía electrostática del sistema descrito en el caso particular $Q = −10 \,\mathrm{nC}$ ?
En la situación particular del apartado anterior, ¿qué trabajo hay que realizar para traer una carga $q$ desde el infinito hasta el punto de posición 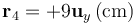$\mathbf{r}_4=+9\mathbf{u}_y\,\mathrm{(cm)}$ . ¿Cuánto vale la fuerza electrostática ejercida sobre dicha carga este punto?
Determine los momentos monopolar y dipolar de la distribución correspondiente al apartado 2. Halle el potencial exacto y el aproximado por el desarrollo multipolar, para el punto 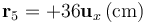$\mathbf{r}_5=+36\mathbf{u}_x\,\mathrm{(cm)}$ . Calcule el error relativo cometido en la aproximación, según la fórmula

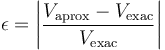
$\epsilon=\left|\frac{V_\mathrm{aprox}-V_\mathrm{exac}}{V_\mathrm{exac}}\right|$

2 Solución

2.1 Punto de campo eléctrico y potencial nulo

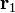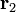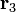Sean tres cargas puntuales $q 1$ , $q 2$ y $q 3$ , situadas en los puntos $P 1$ , $P 2$ y $P 3$ , cuyas posiciones respecto de un punto fijo $O$ (origen de un sistema de referencia), están determiandas por sendos vectores $\mathbf{r}_1$ , $\mathbf{r}_2$ y $\mathbf{r}_3$ . El campo eléctrico y el potencial electrostático creado por el sistema en un punto $P$ , descrito por el radiovector $\mathbf{r}$ , responden a las siguientes expresiones:

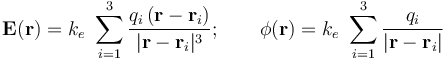
$\mathbf{E}(\mathbf{r})=k_e \ \sum_{i=1}^3\frac{q_i\!\ (\mathbf{r}-\mathbf{r}_i)}{|\mathbf{r}-\mathbf{r}_i|^3}\mathrm{;}\,\qquad\phi(\mathbf{r})=k_e \ \sum_{i=1}^3\frac{q_i}{|\mathbf{r}-\mathbf{r}_i|}$

donde el valor de la constante

k e

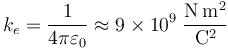en el Sistema Internacional (SI) es, $\displaystyle k_e=\frac{1}{4\pi\varepsilon_0}\approx 9\times 10^9\;\frac{\mathrm{N}\,\mathrm{m}^2}{\mathrm{C}^2}$ .

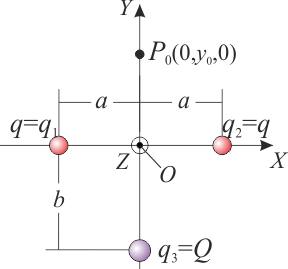
En el sistema bajo estudio hay dos cargas de valor conocido, alineadas en la dirección que definiremos como eje $O X$ del sistema de referencia cartesiano que utilizaremos para la descripción analítica de las magnitudes vectoriales. La tercera carga, de valor no determinado inicialmente, se encuentra en la recta perpendicular al segmento 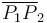$\overline{P_1P}_2$ (cuyos extremos son las otras dos cargas), y que corta a éste en su punto medio $O$ . Tomaremos este punto como origen del sistema de refencia, y a la tercera carga situada en el semieje negativo de $O Y$ . De esta forma se tendrá,

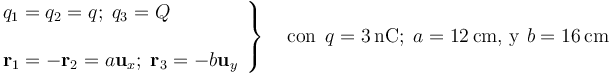
$\left.\begin{array}{l}q_1=q_2=q\mathrm{;}\,\;q_3=Q\\ \\ \mathbf{r}_1=-\mathbf{r}_2=a\mathbf{u}_x\mathrm{;}\,\;\mathbf{r}_3=-b\mathbf{u}_y\end{array}\right\}\quad\mathrm{con}\,\;q=3\,\mathrm{nC;}\;\, a=12\,\mathrm{cm,}\,\,\mathrm{y}\,\, b=16\,\mathrm{cm}$

Para determinar el valor de $Q$ se pide que éste debe ser tal que haya un $P 0$ del eje $O Y$ en que se anulen simultáneamente el campo eléctrico y el potencial creados por el sistema electrostático de tres cargas. La posición de dicho punto vendrá dada por una radiovector 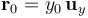$\mathbf{r}_0=y_0\!\ \mathbf{u}_y$ , de componente desconocida. Para calcular los valores de estas incógnitas resolvemos las ecuaciones algebraicas que se obtienen de las siguientes expresiones:

$\left.\begin{array}{l}\displaystyle\mathbf{E}(\mathbf{r}_0)=k_e \!\ \left[\frac{q\!\ (y_0\!\ \mathbf{u}_y-a\!\ \mathbf{u}_x)}{(y_0^2+a^2)^{3/2}}+\frac{q\!\ (y_0\!\ \mathbf{u}_y+a\!\ \mathbf{u}_x)}{(y_0^2+a^2)^{3/2}}+\frac{Q\!\ (y_0+b) \!\ \mathbf{u}_y}{(y_0+b)^3}\right]=\mathbf{0}\\ \\ \displaystyle \phi(\mathbf{r}_0)=k_e \!\ \left[\frac{2\!\ q}{(y_0^2+a^2)^{1/2}}+\frac{Q}{y_0+b}\right]=0\end{array}\right\}\;\Longrightarrow\;\left\{\begin{array}{l}\displaystyle\frac{2\!\ q\!\ y_0}{(y_0^2+a^2)^{3/2}}=-\frac{Q}{(y_0+b)^2}\\ \\ \displaystyle \frac{2\!\ q}{(y_0^2+a^2)^{1/2}}=-\frac{Q}{y_0+b}\end{array}\right.$

Este sistema de ecuaciones se resuelve fácilmente sin mas que dividir la primera ecuación entre la segunda:

$\frac{2\!\ q\!\ y_0\!\ (y_0^2+a^2)^{1/2}}{2\!\ q\!\ (y_0^2+a^2)^{3/2}}=\frac{Q\!\ (y_0+b)}{Q\!\ (y_0+b)^2}\quad\longrightarrow\quad y_0\!\ (y_0+b)=y_0^2+a^2\quad\Longleftrightarrow$ $y_0=\frac{a^2}{b}=9\,\mathrm{cm}$

Revisión de 12:48 18 sep 2012 (ver código fuente) Gabriel (Discusión \| contribuciones) (→Punto de campo eléctrico y potencial nulo) ← Edición más antigua		Revisión de 12:48 18 sep 2012 (ver código fuente) Gabriel (Discusión \| contribuciones) (→Punto de campo eléctrico y potencial nulo) Edición más nueva →
Línea 30:		Línea 30:
	Este sistema de ecuaciones se resuelve fácilmente sin mas que dividir la primera ecuación entre la segunda:		Este sistema de ecuaciones se resuelve fácilmente sin mas que dividir la primera ecuación entre la segunda:

-	<center><math>\frac{2\!\ q\!\ y_0\!\ (y_0^2+a^2)^{1/2}}{2\!\ q\!\ (y_0^2+a^2)^{3/2}}=\frac{Q\!\ (y_0+b)}{Q\!\ (y_0+b)^2}\quad\longrightarrow\quad y_0\!\ (y_0+b)=y_0^2+a^2\quad\Longleftrightarrow</math>{{~~quad~~}}<math> y_0=\frac{a^2}{b}=9\,\mathrm{cm}</math></center>	+	<center><math>\frac{2\!\ q\!\ y_0\!\ (y_0^2+a^2)^{1/2}}{2\!\ q\!\ (y_0^2+a^2)^{3/2}}=\frac{Q\!\ (y_0+b)}{Q\!\ (y_0+b)^2}\quad\longrightarrow\quad y_0\!\ (y_0+b)=y_0^2+a^2\quad\Longleftrightarrow</math>{{qquad}}<math> y_0=\frac{a^2}{b}=9\,\mathrm{cm}</math></center>

Sistema electrostático de tres cargas puntuales

De Laplace

Revisión de 12:48 18 sep 2012

1 Enunciado

2 Solución

2.1 Punto de campo eléctrico y potencial nulo

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES