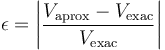Sistema electrostático de tres cargas puntuales
De Laplace
(Diferencias entre revisiones)
(Página creada con '==Enunciado== Un sistema electrostático está formado por tres cargas eléctricas puntuales. Dos de ellas tienen idéntico valor <math>q=3\,\mathrm{nC}</math> y se hallan en lo…') |
(→Enunciado) |
||
| Línea 2: | Línea 2: | ||
Un sistema electrostático está formado por tres cargas eléctricas puntuales. Dos de ellas tienen idéntico valor <math>q=3\,\mathrm{nC}</math> y se hallan en los puntos <math>P_1</math> y <math>P_2</math>, dados por los vectores de posición <math>\mathbf{r}_1=+12\mathbf{u}_x\,\mathrm{(cm)}</math> y <math>\mathbf{r}_2=-12\mathbf{u}_x\,\mathrm{(cm)}</math>, respectivamente. La tercera carga tiene un valor <math>Q</math> y se halla en el punto <math>P_3</math>, dado por <math>\mathbf{r}_3=-16\mathbf{u}_y\,\mathrm{(cm)}</math>. | Un sistema electrostático está formado por tres cargas eléctricas puntuales. Dos de ellas tienen idéntico valor <math>q=3\,\mathrm{nC}</math> y se hallan en los puntos <math>P_1</math> y <math>P_2</math>, dados por los vectores de posición <math>\mathbf{r}_1=+12\mathbf{u}_x\,\mathrm{(cm)}</math> y <math>\mathbf{r}_2=-12\mathbf{u}_x\,\mathrm{(cm)}</math>, respectivamente. La tercera carga tiene un valor <math>Q</math> y se halla en el punto <math>P_3</math>, dado por <math>\mathbf{r}_3=-16\mathbf{u}_y\,\mathrm{(cm)}</math>. | ||
| - | # Determine, si es posible, el valor que debe tener la carga <math>Q</math> y la posición <math>\mathbf{r}_0=y_0\mathbf{u}_y</math> de un punto del | + | # Determine, si es posible, el valor que debe tener la carga <math>Q</math> y la posición <math>\mathbf{r}_0=y_0\mathbf{u}_y</math> de un punto del eje <math>OY</math> en el cuál se anulen simultáneamente el potencial y el campo eléctrico creado por el sistema de tres cargas. |
| - | eje <math>OY</math> en el cuál se anulen simultáneamente el potencial y el campo eléctrico creado por el sistema de tres cargas. | + | |
# ¿Cuál es la energía electrostática del sistema descrito en el caso particular <math>Q = −10 \,\mathrm{nC}</math>? | # ¿Cuál es la energía electrostática del sistema descrito en el caso particular <math>Q = −10 \,\mathrm{nC}</math>? | ||
# En la situación particular del apartado anterior, ¿qué trabajo hay que realizar para traer una carga <math>q</math> desde el infinito hasta el punto de posición <math>\mathbf{r}_4=+9\mathbf{u}_y\,\mathrm{(cm)}</math>. ¿Cuánto vale la fuerza electrostática ejercida sobre dicha carga este punto? | # En la situación particular del apartado anterior, ¿qué trabajo hay que realizar para traer una carga <math>q</math> desde el infinito hasta el punto de posición <math>\mathbf{r}_4=+9\mathbf{u}_y\,\mathrm{(cm)}</math>. ¿Cuánto vale la fuerza electrostática ejercida sobre dicha carga este punto? | ||
# Determine los momentos monopolar y dipolar de la distribución correspondiente al apartado 2. Halle el potencial exacto y el aproximado por el desarrollo multipolar, para el punto <math>\mathbf{r}_5=+36\mathbf{u}_x\,\mathrm{(cm)}</math>. Calcule el error relativo cometido en la aproximación, según la fórmula | # Determine los momentos monopolar y dipolar de la distribución correspondiente al apartado 2. Halle el potencial exacto y el aproximado por el desarrollo multipolar, para el punto <math>\mathbf{r}_5=+36\mathbf{u}_x\,\mathrm{(cm)}</math>. Calcule el error relativo cometido en la aproximación, según la fórmula | ||
| - | + | ||
<center><math>\epsilon=\left|\frac{V_\mathrm{aprox}-V_\mathrm{exac}}{V_\mathrm{exac}}\right|</math></center> | <center><math>\epsilon=\left|\frac{V_\mathrm{aprox}-V_\mathrm{exac}}{V_\mathrm{exac}}\right|</math></center> | ||
| - | |||
Revisión de 23:47 17 sep 2012
Enunciado
Un sistema electrostático está formado por tres cargas eléctricas puntuales. Dos de ellas tienen idéntico valor 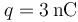 y se hallan en los puntos P1 y P2, dados por los vectores de posición
y se hallan en los puntos P1 y P2, dados por los vectores de posición 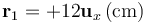 y
y 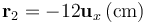 , respectivamente. La tercera carga tiene un valor Q y se halla en el punto P3, dado por
, respectivamente. La tercera carga tiene un valor Q y se halla en el punto P3, dado por 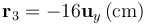 .
.
- Determine, si es posible, el valor que debe tener la carga Q y la posición
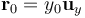 de un punto del eje OY en el cuál se anulen simultáneamente el potencial y el campo eléctrico creado por el sistema de tres cargas.
de un punto del eje OY en el cuál se anulen simultáneamente el potencial y el campo eléctrico creado por el sistema de tres cargas.
- ¿Cuál es la energía electrostática del sistema descrito en el caso particular
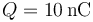 ?
?
- En la situación particular del apartado anterior, ¿qué trabajo hay que realizar para traer una carga q desde el infinito hasta el punto de posición
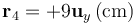 . ¿Cuánto vale la fuerza electrostática ejercida sobre dicha carga este punto?
. ¿Cuánto vale la fuerza electrostática ejercida sobre dicha carga este punto?
- Determine los momentos monopolar y dipolar de la distribución correspondiente al apartado 2. Halle el potencial exacto y el aproximado por el desarrollo multipolar, para el punto
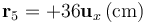 . Calcule el error relativo cometido en la aproximación, según la fórmula
. Calcule el error relativo cometido en la aproximación, según la fórmula