Entrar Página Discusión Historial Go to the site toolbox

Problemas de metrología (G.I.T.I.)

De Laplace

(Diferencias entre revisiones)
Línea 1: Línea 1:
-
==[[Ejemplos de análisis dimensional (Prob.1.1)]]==
+
==[[Ejemplos de análisis dimensional]]==
A partir de las relaciones definitorias
A partir de las relaciones definitorias
Línea 27: Línea 27:
determine las ecuaciones dimensionales de estas magnitudes, así como sus unidades en el Sistema Internacional (SI) en función de las unidades básicas de este sistema.
determine las ecuaciones dimensionales de estas magnitudes, así como sus unidades en el Sistema Internacional (SI) en función de las unidades básicas de este sistema.
-
==[[Ecuación dimensional de G (Prob.1.2) (Ex.Nov/11)]]==
+
==[[Ecuación dimensional de G (Ex.Nov/11)]]==
La ley de la Gravitación Universal establece que la interacción gravitatoria entre dos cuerpos puede expresarse mediante una fuerza
La ley de la Gravitación Universal establece que la interacción gravitatoria entre dos cuerpos puede expresarse mediante una fuerza
cuyo módulo es directamente proporcional al producto de las masas de los cuerpos (<math>m_1\,</math> y <math>m_2\,</math>) e inversamente proporcional al cuadrado de la distancia (<math>r\,</math>) que los separa, es decir:
cuyo módulo es directamente proporcional al producto de las masas de los cuerpos (<math>m_1\,</math> y <math>m_2\,</math>) e inversamente proporcional al cuadrado de la distancia (<math>r\,</math>) que los separa, es decir:
Línea 36: Línea 36:
universal <math>G\,</math> en el SI?
universal <math>G\,</math> en el SI?
-
==[[Fórmulas dimensionalmente incorrectas (Prob.1.3)]]==
+
==[[Fórmulas dimensionalmente incorrectas]]==
Teniendo en cuenta las dimensiones calculadas en el problema 1.1, indique cuáles de las siguientes expresiones son necesariamente incorrectas (los símbolos son los usuales en mecánica):
Teniendo en cuenta las dimensiones calculadas en el problema 1.1, indique cuáles de las siguientes expresiones son necesariamente incorrectas (los símbolos son los usuales en mecánica):
Línea 55: Línea 55:
:h) <math>\int_{t_1}^{t_2}\frac{P-\vec{v}\cdot(\vec{a}+\vec{p}/m)}{v^2}\,\mathrm{d}t = \frac{m(t-2/t)}{v}</math>
:h) <math>\int_{t_1}^{t_2}\frac{P-\vec{v}\cdot(\vec{a}+\vec{p}/m)}{v^2}\,\mathrm{d}t = \frac{m(t-2/t)}{v}</math>
-
==[[Dependencias del periodo de un péndulo (Prob.1.4)]]==
+
==[[Dependencias del periodo de un péndulo]]==
Un péndulo simple es una masa <math>m</math> suspendida de un hilo ideal (sin masa), que tiene una longitud <math>l</math>. La masa está sometida a la aceleración de la gravedad, <math>g</math>. El péndulo llega a separarse de la vertical un cierto ángulo <math>\theta_0</math>.
Un péndulo simple es una masa <math>m</math> suspendida de un hilo ideal (sin masa), que tiene una longitud <math>l</math>. La masa está sometida a la aceleración de la gravedad, <math>g</math>. El péndulo llega a separarse de la vertical un cierto ángulo <math>\theta_0</math>.
Si duplicamos la longitud del péndulo, ¿cómo cambiará su periodo de oscilación? ¿Y si nos llevamos el péndulo a la Luna, donde la gravedad es 1/6 de la terrestre?
Si duplicamos la longitud del péndulo, ¿cómo cambiará su periodo de oscilación? ¿Y si nos llevamos el péndulo a la Luna, donde la gravedad es 1/6 de la terrestre?
-
==[[Dependencias de la fuerza centrípeta (Prob.1.5)]]==
+
==[[Dependencias de la fuerza centrípeta]]==
Se sabe que la fuerza centrípeta solo depende de la masa, la velocidad y el radio de curvatura. Determine la fórmula que da la fuerza centrípeta en función de estas tres cantidades.
Se sabe que la fuerza centrípeta solo depende de la masa, la velocidad y el radio de curvatura. Determine la fórmula que da la fuerza centrípeta en función de estas tres cantidades.
-
==[[Dependencias de la fuerza viscosa (Prob.1.6) (Ex.Nov/11)]]==
+
==[[Dependencias de la fuerza viscosa (Ex.Nov/11)]]==
El poise (P), que es la unidad de viscosidad dinámica en el sistema CGS, se define como 1 P = 1 g<math>\cdot</math>(s<math>\cdot</math>cm)<math>^{-1}</math>. ¿Cuál es la unidad de viscosidad dinámica en el SI?
El poise (P), que es la unidad de viscosidad dinámica en el sistema CGS, se define como 1 P = 1 g<math>\cdot</math>(s<math>\cdot</math>cm)<math>^{-1}</math>. ¿Cuál es la unidad de viscosidad dinámica en el SI?
Línea 72: Línea 72:
:b) Si, al pasar de un instante <math>t_1\,</math> a otro posterior <math>t_2\,</math>, la celeridad de una esfera en el seno de un fluido se ha reducido conforme a la relación <math>v_2=0.80\,v_1\,</math>, ¿cómo habrá cambiado el módulo de la fuerza viscosa sobre ella ejercida?
:b) Si, al pasar de un instante <math>t_1\,</math> a otro posterior <math>t_2\,</math>, la celeridad de una esfera en el seno de un fluido se ha reducido conforme a la relación <math>v_2=0.80\,v_1\,</math>, ¿cómo habrá cambiado el módulo de la fuerza viscosa sobre ella ejercida?
-
==[[Ejemplos de conversión de unidades (Prob.1.7)]]==
+
==[[Ejemplos de conversión de unidades]]==
Exprese estas cantidades en términos de las unidades fundamentales del SI:
Exprese estas cantidades en términos de las unidades fundamentales del SI:

Revisión de 18:41 17 sep 2012

Contenido

1 Ejemplos de análisis dimensional

A partir de las relaciones definitorias

Velocidad Cantidad de movimiento Aceleración Fuerza
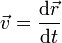
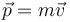
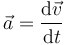
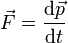
\vec{v}=\frac{\mathrm{d}\vec{r}}{\mathrm{d}t} \vec{p}=m\vec{v} \vec{a}=\frac{\mathrm{d}\vec{v}}{\mathrm{d}t} \vec{F}=\frac{\mathrm{d}\vec{p}}{\mathrm{d}t}
Trabajo Potencia Momento cinético Momento de una fuerza
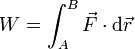
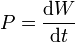
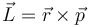
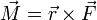
W=\int_A^B\vec{F}\cdot\mathrm{d}\vec{r} P=\frac{\mathrm{d}W}{\mathrm{d}t} \vec{L}=\vec{r}\times\vec{p} \vec{M}=\vec{r}\times\vec{F}

determine las ecuaciones dimensionales de estas magnitudes, así como sus unidades en el Sistema Internacional (SI) en función de las unidades básicas de este sistema.

2 Ecuación dimensional de G (Ex.Nov/11)

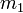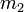La ley de la Gravitación Universal establece que la interacción gravitatoria entre dos cuerpos puede expresarse mediante una fuerza cuyo módulo es directamente proporcional al producto de las masas de los cuerpos (m_1\, y m_2\,) e inversamente proporcional al cuadrado de la distancia (r\,) que los separa, es decir:

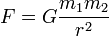
F=G\frac{m_1m_2}{r^2}

¿Cuál es la ecuación dimensional de la constante de gravitación universal 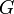G\, en el SI?

3 Fórmulas dimensionalmente incorrectas

Teniendo en cuenta las dimensiones calculadas en el problema 1.1, indique cuáles de las siguientes expresiones son necesariamente incorrectas (los símbolos son los usuales en mecánica):

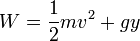
a) W = \frac{1}{2}mv^2 + gy
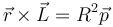
b) \vec{r}\times\vec{L} = R^2\vec{p}
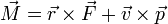
c) \vec{M} = \vec{r}\times\vec{F}+\vec{v}\times\vec{p}
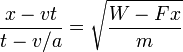
d) \frac{x-vt}{t-v/a} = \sqrt{\frac{W-Fx}{m}}
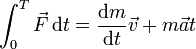
e) \int_0^T \vec{F}\,\mathrm{d}t = \frac{\mathrm{d}m}{\mathrm{d}t}\vec{v}+ m\vec{a}t
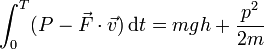
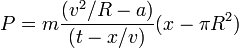
f) \int_0^T (P-\vec{F}\cdot\vec{v})\,\mathrm{d}t = mgh + \frac{p^2}{2m}
g) P = m\frac{(v^2/R - a)}{(t-x/v)}(x-\pi R^2)
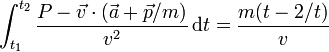
h) \int_{t_1}^{t_2}\frac{P-\vec{v}\cdot(\vec{a}+\vec{p}/m)}{v^2}\,\mathrm{d}t = \frac{m(t-2/t)}{v}

4 Dependencias del periodo de un péndulo

Un péndulo simple es una masa m suspendida de un hilo ideal (sin masa), que tiene una longitud l. La masa está sometida a la aceleración de la gravedad, g. El péndulo llega a separarse de la vertical un cierto ángulo θ0.

Si duplicamos la longitud del péndulo, ¿cómo cambiará su periodo de oscilación? ¿Y si nos llevamos el péndulo a la Luna, donde la gravedad es 1/6 de la terrestre?

5 Dependencias de la fuerza centrípeta

Se sabe que la fuerza centrípeta solo depende de la masa, la velocidad y el radio de curvatura. Determine la fórmula que da la fuerza centrípeta en función de estas tres cantidades.

6 Dependencias de la fuerza viscosa (Ex.Nov/11)

El poise (P), que es la unidad de viscosidad dinámica en el sistema CGS, se define como 1 P = 1 g\cdot(s\cdotcm) − 1. ¿Cuál es la unidad de viscosidad dinámica en el SI?

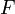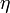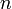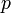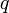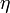Según la denominada ley de Stokes, el módulo de la fuerza viscosa F\, ejercida sobre una esfera que se mueve en un fluido depende exclusivamente de tres magnitudes: el radio r\, de la esfera, la celeridad v\, con que ésta se mueve y la viscosidad dinámica \eta\, del fluido. Deduzca, mediante análisis dimensional, los exponentes n\,, p\, y q\, con los que aparecen r\,, v\, y \eta\,, respectivamente, en la fórmula del módulo de la fuerza viscosa según Stokes, y así podrá responder a las dos siguientes preguntas.

a) Si en un mismo fluido se mueven dos esferas, ambas con igual celeridad, pero el radio de la segunda es el doble que el radio de la primera (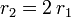r_2=2\,r_1\,), ¿qué relación existe entre los módulos de las fuerzas viscosas soportadas por la primera y la segunda esfera?
b) Si, al pasar de un instante 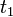t_1\, a otro posterior 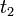t_2\,, la celeridad de una esfera en el seno de un fluido se ha reducido conforme a la relación 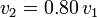v_2=0.80\,v_1\,, ¿cómo habrá cambiado el módulo de la fuerza viscosa sobre ella ejercida?

7 Ejemplos de conversión de unidades

Exprese estas cantidades en términos de las unidades fundamentales del SI:

  1. Nudo (milla náutica/hora)
  2. Año luz
  3. Acre (rectángulo de 66 pies por 220 yardas)
  4. Siglo
  5. Unidad de Masa Atómica
  6. R = 0.082 atm·L/K·mol
  7. Libra-fuerza por pulgada cuadrada (Ex.Ene/11)

8 Conversión del slug (Ex.Nov/11)

La unidad de masa en el sistema FPS es el slug, que se define como la masa que se acelera un pie por segundo cada segundo bajo la acción de una libra-fuerza (1 slug = 1 lbf\cdots2/ft). Si una pulgada son 2.54 cm, un pie (ft) tiene 12 pulgadas, y una libra-fuerza (lbf) son 4.448 N, ¿a cuánto equivalen 5 slugs en el SI?

Obtenido de "http://tesla.us.es/wiki/index.php/Problemas_de_metrolog%C3%ADa_(G.I.T.I.)"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace