1.5. Dependencias de la fuerza centrípeta
De Laplace
1 Enunciado
Se sabe que la fuerza centrípeta solo depende de la masa, la velocidad y el radio de curvatura. Determine la fórmula que da la fuerza centrípeta en función de estas tres cantidades.
2 Solución
Se nos dice que
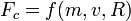
y nada más. Debido a la homogeneidad dimensional, f no puede ser una función arbitraria, sino que debe dar como resultado una fuerza. Se trata entonces de ver con qué producto de potencias de estas tres variables se llega a las dimensiones de una fuerza. Tenemos la ecuación dimensional

Igualando los exponentes obtenemos
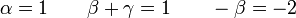
de donde
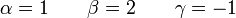
y por tanto la fuerza centrípeta es de la forma
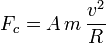
donde A es una cierta cantidad adimensional, esto es, un número. Esta expresión no nos dice cuanto vale la fuerza centrípeta (ya que no sabemos el valor de A, que podría ser 2, 19, -1, -3704 o cualquier otro), pero sí como depende de la masa, la velocidad y el radio de curvatura y por tanto nos permite comparar su valor cuando modificamos alguna de estas variables. Por ejemplo, si se nos dice que la velocidad se multiplica por 2, sabemos que la fuerza centrípeta debe multiplicarse por 4.





