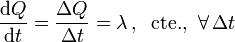Tubería calentada con flujo de líquido GIA

De Laplace

Revisión de 17:49 6 jun 2012 (ver código fuente) Gabriel (Discusión | contribuciones) (→Solución) ← Edición más antigua		Revisión de 17:51 6 jun 2012 (ver código fuente) Gabriel (Discusión | contribuciones) (→Solución) Edición más nueva →
Línea 8:		Línea 8:
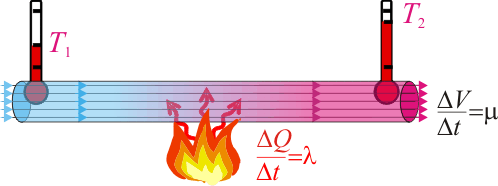
-	<center><math>\forall\, \Delta t\,\mathrm{,}\,\;\; \frac{\Delta Q}{\Delta t}=\frac{\mathrm{d}Q}{\mathrm{d}t}=\lambda\,\mathrm{,}\,\;\;\mathrm{cte.}</math></center>	+	<center><math>\frac{\mathrm{d}Q}{\mathrm{d}t}=\frac{\Delta Q}{\Delta t}=\lambda\,\mathrm{,}\,\;\;\mathrm{cte.,}\;\;\forall\, \Delta t</math></center>

---

Revisión de 17:51 6 jun 2012

1 Enunciado

Por una tubería calentada en su punto medio con una llama invariable fluyen 50 l de agua por segundo. La temperatura de entrada es de 20 °C, y la de salida de 35 °C. Otro líquido de densidad 0.8, circula a continuación por el mismo tubo calentado por la misma llama, pero con un caudal de 25 l/s. Las temperaturas en los dos extremos se estacionan ahora en 18 °C y en 68 °C. Calcular el calor específico del líquido.

2 Solución

El dato de que la llama es invariable debemos intepretarlo en el sentido de que, en intervalos iguales de tiempo, la llama suministra la idénticas cantidades de calor. O lo que es lo mismo, la cantidad de calor que suministra por unidad de tiempo es un valor constante: