Entrar Página Discusión Historial Go to the site toolbox

Calibración de un termistor GIA

De Laplace

(Diferencias entre revisiones)
(→Variación de la resistencia con la temperatura)
(→Variación de la resistencia con la temperatura)
 
Línea 100: Línea 100:
</center>
</center>
Cuando el módulo de la derivada es mayor, un <math>\mathrm{d}T </math> pequeño induce un <math>\mathrm{d}R </math> más grande.
Cuando el módulo de la derivada es mayor, un <math>\mathrm{d}T </math> pequeño induce un <math>\mathrm{d}R </math> más grande.
-
[[Categoría:Problemas de temperatura|0]]
+
[[Categoría:Problemas de temperatura y Principio 0 F2 GIA]]
-
[[Categoría:Temperatura y Principio cero]]
+

última version al 10:35 6 jun 2012

Contenido

1 Enunciado

Un termistor es un dispositivo de estado sólido cuya resistencia varía considerablemente con la temperatura. Esta dependencia viene descrita aproximadamente por la expresión R = R0eB / T, donde R se expresa en ohmios(Ω), T en kelvins y R0 y B son constantes que pueden determinarse midiendo R para puntos de calibración conocidos.

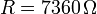  1. Si R=7360\,\mathrm{\Omega} en el punto de congelación del hielo y 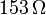153\,\mathrm{\Omega} en el punto de ebullición del agua, calcula R0 y B.
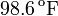  2. ¿Cuál es la resistencia del termistor a 98.6\,\mathrm{^oF}?
  3. ¿Cuál es la variación de la resistencia con la temperatura (dR / dT) en el punto de congelación del hielo y el de ebullición del agua?
  4. ¿Para cual de estas temperaturas es este termistor más sensible?

2 Solución

2.1 Calibración del termistor

La relación entre la propiedad termométrica (la resistencia) y la temperatura tiene dos constantes: R0 y B. Necesitamos dos puntos de calibración.

En el punto de fusión del hielo tenemos

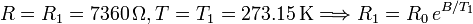
R=R_1=7360\,\mathrm{\Omega}, T=T_1=273.15\,\mathrm{K} \Longrightarrow R_1= R_0\,e^{B/T_1}

En el punto de ebullición del agua tenemos

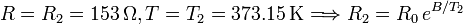
R=R_2=153\,\mathrm{\Omega}, T=T_2=373.15\,\mathrm{K} \Longrightarrow R_2= R_0\,e^{B/T_2}

Dividiendo una por otra obtenemos

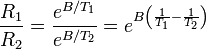
\dfrac{R_1}{R_2} = \dfrac{e^{B/T_1}}{e^{B/T_2}} = e^{B\left(\frac{1}{T_1}-\frac{1}{T_2}\right)}

Tomando logaritmos

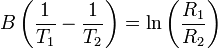
B\left(\frac{1}{T_1}-\frac{1}{T_2}\right) = \ln\left(\dfrac{R_1}{R_2}\right)

Despejando llegamos a

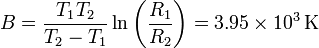
B = \dfrac{T_1T_2}{T_2-T_1}\ln\left(\dfrac{R_1}{R_2}\right) =3.95\times10^{3}\,\mathrm{K}

Despejamos R0 de una de las dos ecuaciones

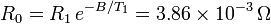
R_0 = R_1\,e^{-B/T_1} = 3.86\times10^{-3}\,\Omega

2.2 Resistencia para una temperatura dada

Pasamos la temperatura a la escala Celsius

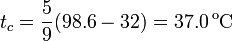
t_c = \dfrac{5}{9}(98.6-32) = 37.0\,\mathrm{^oC}

La temperatura absoluta es

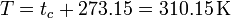
T = t_c + 273.15 = 310.15\,\mathrm{K}

La resistencia es

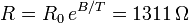
R = R_0\,e^{B/T} = 1311\,\mathrm{\Omega}

2.3 Variación de la resistencia con la temperatura

La derivada es

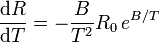
\dfrac{\mathrm{d}R}{\mathrm{d}T} = -\dfrac{B}{T^2}R_0\,e^{B/T}

En los puntos de calibración tenemos

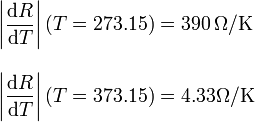
\begin{array}{l} \left|\dfrac{\mathrm{d}R}{\mathrm{d}T}\right|(T=273.15) = 390\,\mathrm{\Omega/K} \\ \\ \left|\dfrac{\mathrm{d}R}{\mathrm{d}T}\right|(T=373.15) = 4.33\mathrm{\Omega/K} \end{array}

La sensibilidad es mayor donde el módulo de la derivada es más grande. La variación de resistencia debida a una variación de temperatura es

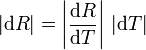
|\mathrm{d}R| = \left|\dfrac{\mathrm{d}R}{\mathrm{d}T}\right|\,|\mathrm{d}T|

Cuando el módulo de la derivada es mayor, un dT pequeño induce un dR más grande.

Obtenido de "http://tesla.us.es/wiki/index.php/Calibraci%C3%B3n_de_un_termistor_GIA"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Esta página fue modificada por última vez el 10:35, 6 jun 2012. - Esta página ha sido visitada 6.294 veces. - Aviso legal - Acerca de Laplace