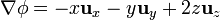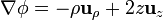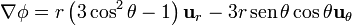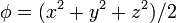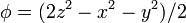Entrar Página Discusión Historial Go to the site toolbox

Cálculo de gradientes

De Laplace

(Diferencias entre revisiones)
(→Segundo campo)
(→Primer campo)
 
(Una edición intermedia no se muestra.)
Línea 16: Línea 16:
Vemos que el resultado no es otro que el vector de posición.
Vemos que el resultado no es otro que el vector de posición.
-
Para calcularlo en cilíndricas, empleamos la expresión de este campo que calculamos en el problema \theboletin.\ref{CampoEscalar}.
+
Para calcularlo en cilíndricas, empleamos la expresión de este campo que calculamos en [[Campos escalares en diferentes sistemas|otro problema]].
<center><math>\phi = \frac{\rho^2+z^2}{2}</math></center>
<center><math>\phi = \frac{\rho^2+z^2}{2}</math></center>
Línea 44: Línea 44:
===Segundo campo===
===Segundo campo===
-
Para el segundo campo operamos de forma análoga, empleando las expresiones calculadas en [[otro problema]]
+
Para el segundo campo operamos de forma análoga, empleando las expresiones calculadas en [[Campos escalares en diferentes sistemas|otro problema]]
<center><math>\nabla\phi = -x\mathbf{u}_{x}-y\mathbf{u}_{y}+2z\mathbf{u}_{z}</math></center>
<center><math>\nabla\phi = -x\mathbf{u}_{x}-y\mathbf{u}_{y}+2z\mathbf{u}_{z}</math></center>

última version al 11:07 23 sep 2008

Contenido

1 Enunciado

Para los campos escalares

  1. \phi = (x^2+y^2+z^2)/2\,
  2. \phi = (2z^2-x^2-y^2)/2\,

calcule su gradiente en coordenadas cartesianas, cilíndricas y esféricas.

2 Solución

2.1 Primer campo

El gradiente del primer campo, calculado en cartesianas es

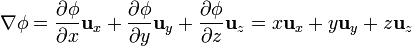
\nabla\phi = \frac{\partial \phi}{\partial x}\mathbf{u}_{x}+\frac{\partial \phi}{\partial y}\mathbf{u}_{y}+\frac{\partial \phi}{\partial z}\mathbf{u}_{z}=x\mathbf{u}_{x}+y\mathbf{u}_{y}+z\mathbf{u}_{z}

Vemos que el resultado no es otro que el vector de posición.

Para calcularlo en cilíndricas, empleamos la expresión de este campo que calculamos en otro problema.

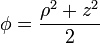
\phi = \frac{\rho^2+z^2}{2}


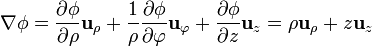
\nabla\phi = \frac{\partial \phi}{\partial \rho}\mathbf{u}_{\rho}+\frac{1}{\rho}\frac{\partial \phi}{\partial \varphi}\mathbf{u}_{\varphi}+\frac{\partial \phi}{\partial z}\mathbf{u}_{z} = \rho\mathbf{u}_{\rho}+z\mathbf{u}_{z}

Y, en esféricas,

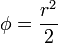
\phi = \frac{r^2}{2}
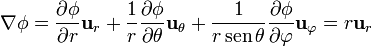
\nabla\phi = \frac{\partial \phi}{\partial r}\mathbf{u}_{r}+\frac{1}{r}\frac{\partial \phi}{\partial \theta}\mathbf{u}_{\theta}+\frac{1}{r\,\mathrm{sen}\,\theta}\frac{\partial \phi}{\partial \varphi}\mathbf{u}_{\varphi} = r\mathbf{u}_{r}

De estos resultados obtenemos tres expresiones equivalentes para el vector de posición

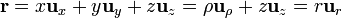
\mathbf{r} = x\mathbf{u}_{x}+y\mathbf{u}_{y}+z\mathbf{u}_{z} = \rho\mathbf{u}_{\rho}+z\mathbf{u}_{z} = r\mathbf{u}_{r}

y, comparando las dos primeras,

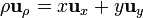
\rho\mathbf{u}_{\rho}=x\mathbf{u}_{x}+y\mathbf{u}_{y}

2.2 Segundo campo

Para el segundo campo operamos de forma análoga, empleando las expresiones calculadas en otro problema

\nabla\phi = -x\mathbf{u}_{x}-y\mathbf{u}_{y}+2z\mathbf{u}_{z}


\nabla\phi = -\rho\mathbf{u}_{\rho}+2z\mathbf{u}_{z}


\nabla\phi = r\left(3\cos^2\theta-1\right)\mathbf{u}_{r}-3r\,\mathrm{sen}\,\theta\cos\theta\mathbf{u}_{\theta}
Obtenido de "http://tesla.us.es/wiki/index.php/C%C3%A1lculo_de_gradientes"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Esta página fue modificada por última vez el 11:07, 23 sep 2008. - Esta página ha sido visitada 15.376 veces. - Aviso legal - Acerca de Laplace