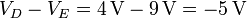Sistema de cuatro condensadores

De Laplace

(Diferencias entre revisiones)

Revisión de 18:26 14 may 2012

1 Enunciado

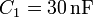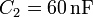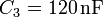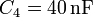El circuito de la figura está formado por cuatro condensadores cuyas capacidades son: $C_1=30\,\mathrm{nF}$ , $C_2=60\,\mathrm{nF}$ , $C_3=120\,\mathrm{nF}$ y $C_4=40\,\mathrm{nF}$ . La diferencia de potencial entre A y B es de 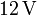$12\,\mathrm{V}$ . ¿Qué diferencia de potencial mide un voltímetro situado entre los puntos D y E? Calcule la carga de cada condensador y la diferencia de potencial entre las placas de cada uno, así como la energía almacenada en el sistema.

Suponga que, sin desconectar la fuente, se cierra el interruptor entre los puntos D y E. Tras la conexión, ¿cuánto valen las cargas, los voltajes y la energía almacenada?

2 Antes de la conexión

Tenemos que, para cada uno de los condensadores de la rama superior se cumple

$V_A-V_D = \frac{Q_1}{C_1}\qquad\qquad V_D-V_B = \frac{Q_2}{C_2}$

pero, por estar el punto D desconectado de cualquier otra fuente o elemento, los dos condensadores $C 1$ y $C 2$ están en serie y la carga en ambos es la misma

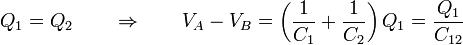
$Q_1 = Q_2\qquad\Rightarrow\qquad V_A-V_B = \left(\frac{1}{C_1}+\frac{1}{C_2}\right)Q_1 = \frac{Q_1}{C_{12}}$

siendo $C 12$ la capacidad del condensador equivalente. Puesto que conocemos la diferencia de potencial total y la capacidad de cada condensador, podemos hallar la carga en cada uno

No se pudo entender (Falta el ejecutable de <strong>texvc</strong>. Por favor, lea <em>math/README</em> para configurarlo.): \frac{1}{C_{12}}=\frac{1}{C_1}+\frac{1}{C_2}\qquad\Rightarrrow\qquad C_{12}=20\,\mathrm{nF}\qquad\Rightarrow\qquad Q_1 = Q_2 = C_{12}\,(V_A-V_B) = 240\,\mathrm{nC}

Una vez que tenemos la carga en cada uno, podemos hallar las respectivas diferencias de potencial

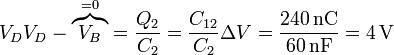
$V_D V_D-\overbrace{V_B}^{=0} = \frac{Q_2}{C_2}=\frac{C_{12}}{C_2}\Delta V = \frac{240\,\mathrm{nC}}{60\,\mathrm{nF}}=4\,\mathrm{V}$

Operando del mismo modo hallamos la carga de los condensadores de la rama inferior

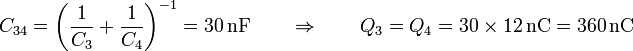
$C_{34}=\left(\frac{1}{C_3}+\frac{1}{C_4}\right)^{-1}= 30\,\mathrm{nF}\qquad\Rightarrow\qquad Q_3 = Q_4 = 30\times 12\,\mathrm{nC} =360\,\mathrm{nC}$

y el voltaje del punto E

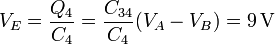
$V_E = \frac{Q_4}{C_4}=\frac{C_{34}}{C_4}(V_A-V_B) = 9\,\mathrm{V}$

Por tanto la diferencia de potencial entre ambos puntos es

$V_D - V_E = 4\,\mathrm{V}-9\,\mathrm{V}=-5\,\mathrm{V}$

3 Después de la conexión

@@ Línea 13: / Línea 13: @@
 pero, por estar el punto D desconectado de cualquier otra fuente o elemento, los dos condensadores <math>C_1</math> y <math>C_2</math> están en serie y la carga en ambos es la misma
-<center><math>Q_1 = Q_2\qqquad\Rightarrow\qquad V_A-V_B = \left(\frac{1}{C_1}+\frac{1}{C_2}\right)Q_1 = \frac{Q_1}{C_{12}}</math></center>
+<center><math>Q_1 = Q_2\qquad\Rightarrow\qquad V_A-V_B = \left(\frac{1}{C_1}+\frac{1}{C_2}\right)Q_1 = \frac{Q_1}{C_{12}}</math></center>
 siendo <math>C_{12}</math> la capacidad del condensador equivalente. Puesto que conocemos la diferencia de potencial total y la capacidad de cada condensador, podemos hallar la carga en cada uno
@@ Línea 34: / Línea 34: @@
 <center><math>V_D - V_E = 4\,\mathrm{V}-9\,\mathrm{V}=-5\,\mathrm{V}</math></center>
 ==Después de la conexión==
 [[Categoría:Problemas de electrostática en medios materiales (GIE)]]

Sistema de cuatro condensadores

De Laplace

Revisión de 18:26 14 may 2012

1 Enunciado

2 Antes de la conexión

3 Después de la conexión

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES