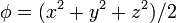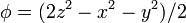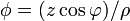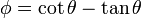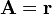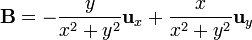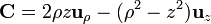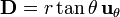Problemas de fundamentos matemáticos
De Laplace
(Diferencias entre revisiones)
(Nueva página: ==Campos escalares en diferentes sistemas Exprese los siguientes campos escalares en coordenadas cartesianas, cilíndricas y esféricas # <math>\phi = (x^2+y^2+z^2)/2\,</math> # <mat...) |
|||
| Línea 1: | Línea 1: | ||
| - | ==Campos escalares en diferentes sistemas | + | ==[[Campos escalares en diferentes sistemas]]== |
Exprese los siguientes campos escalares en coordenadas cartesianas, cilíndricas y esféricas | Exprese los siguientes campos escalares en coordenadas cartesianas, cilíndricas y esféricas | ||
| Línea 5: | Línea 5: | ||
# <math>\phi = (2z^2-x^2-y^2)/2\,</math> | # <math>\phi = (2z^2-x^2-y^2)/2\,</math> | ||
# <math>\phi = (z\cos\varphi)/\rho</math> | # <math>\phi = (z\cos\varphi)/\rho</math> | ||
| - | # <math>\phi = \cot\theta - \tan\theta</math> | + | # <math>\phi = \cot\theta - \tan\theta\,</math> |
| + | |||
| + | ==[[Campos vectoriales en diferentes sistemas]]== | ||
| + | Exprese los siguientes campos vectoriales en coordenadas cartesianas, cilíndricas y esféricas: | ||
| + | |||
| + | # <math>\mathbf{A} = \mathbf{r}\,</math> | ||
| + | # <math>\mathbf{B} = -\dfrac{y}{x^2+y^2}\mathbf{u}_{x}+\dfrac{x}{x^2+y^2}\mathbf{u}_{y}</math> | ||
| + | # <math>\mathbf{C} = 2\rho z\mathbf{u}_{\rho}-(\rho^2-z^2)\mathbf{u}_{z}</math> | ||
| + | # <math>\mathbf{D}=r\tan\theta\,\mathbf{u}_{\theta}</math> | ||
Revisión de 08:30 23 sep 2008
1 Campos escalares en diferentes sistemas
Exprese los siguientes campos escalares en coordenadas cartesianas, cilíndricas y esféricas
2 Campos vectoriales en diferentes sistemas
Exprese los siguientes campos vectoriales en coordenadas cartesianas, cilíndricas y esféricas: