Problemas de corriente eléctrica (GIA)
De Laplace
(Diferencias entre revisiones)
(→Asociación de resistencia independiente de la temperatura) |
(→Asociación de resistencia independiente de la temperatura) |
||
| Línea 1: | Línea 1: | ||
| - | ==[[Asociación de resistencias independiente de la temperatura GIA|Asociación de | + | ==[[Asociación de resistencias independiente de la temperatura GIA|Asociación de resistencias independiente de la temperatura]]== |
Un cable de cobre de sección transversal <math>A</math> y longitud <math>l_\mathrm{Cu}</math> se conecta en serie con un cable de carbono de la misma sección transversal y longitud <math>l_\mathrm{C}</math>. Halle la relación de las longitudes de ambos cables para que la resistencia total del dispositivo sea independiente de la temperatura. Explicar por qué esta relación | Un cable de cobre de sección transversal <math>A</math> y longitud <math>l_\mathrm{Cu}</math> se conecta en serie con un cable de carbono de la misma sección transversal y longitud <math>l_\mathrm{C}</math>. Halle la relación de las longitudes de ambos cables para que la resistencia total del dispositivo sea independiente de la temperatura. Explicar por qué esta relación | ||
sólo asegura independencia de la resistencia con la <math>R</math> con la temperatura para pequeñas variaciones de dicha magnitud. | sólo asegura independencia de la resistencia con la <math>R</math> con la temperatura para pequeñas variaciones de dicha magnitud. | ||
'''Datos''': <math>\rho_\mathrm{Cu}^0=1.7\times10^{-8}\,\Omega\,\mathrm{m}\,\mathrm{;}\,</math> <math>\rho_\mathrm{C}^0=3500\times10^{-8}\,\Omega\,\mathrm{m}\,\mathrm{;}</math> <math>\alpha_\mathrm{Cu}=3.9\times10^{-3}\,\mbox{K}^{-1}\,\mathrm{;}\,</math> <math>\alpha_\mathrm{C}=-0.5\times10^{-3}\,\mbox{K}^{-1}</math>. | '''Datos''': <math>\rho_\mathrm{Cu}^0=1.7\times10^{-8}\,\Omega\,\mathrm{m}\,\mathrm{;}\,</math> <math>\rho_\mathrm{C}^0=3500\times10^{-8}\,\Omega\,\mathrm{m}\,\mathrm{;}</math> <math>\alpha_\mathrm{Cu}=3.9\times10^{-3}\,\mbox{K}^{-1}\,\mathrm{;}\,</math> <math>\alpha_\mathrm{C}=-0.5\times10^{-3}\,\mbox{K}^{-1}</math>. | ||
Revisión de 12:29 1 abr 2012
Asociación de resistencias independiente de la temperatura
Un cable de cobre de sección transversal A y longitud lCu se conecta en serie con un cable de carbono de la misma sección transversal y longitud lC. Halle la relación de las longitudes de ambos cables para que la resistencia total del dispositivo sea independiente de la temperatura. Explicar por qué esta relación sólo asegura independencia de la resistencia con la R con la temperatura para pequeñas variaciones de dicha magnitud.
Datos: 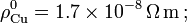
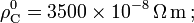
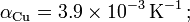
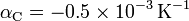 .
.





