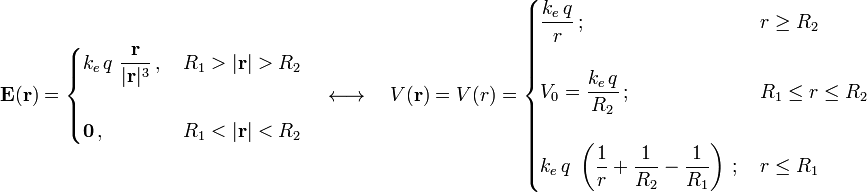Esfera conductora hueca con carga puntual GIA
De Laplace
(→Carga eléctrica en las superficies del conductor) |
(→Expresiones en todo el espacio) |
||
| (71 ediciones intermedias no se muestran.) | |||
| Línea 11: | Línea 11: | ||
<center>[[Archivo:q_en_cond_1.gif]]</center> | <center>[[Archivo:q_en_cond_1.gif]]</center> | ||
| - | definido en todos los puntos del espacio. Si la carga puntual, que supondremos positiva, se encuentra en el hueco de la esfera conductora, este campo eléctrico arrastrará las cargas libres negativas del conductor hacia la superficie interior <math>\Sigma_\mathrm{int}:\ r=R_1</math>, a la vez que desplazaría las posibles cargas libres positivas hacia la exterior, <math>\Sigma_\mathrm{ext}:\ r=R_2</math>, induciéndose en dichas superficies sendas densidades superficiales de carga de signo opuesto. | + | definido en todos los puntos del espacio. Si la carga puntual, que supondremos positiva, se encuentra en el hueco de la esfera conductora, este campo eléctrico arrastrará las cargas libres negativas del conductor hacia la superficie interior <math>\Sigma_\mathrm{int}:\ r=R_1</math>, a la vez que desplazaría las posibles cargas libres positivas hacia la exterior, <math>\Sigma_\mathrm{ext}:\ r=R_2</math>, induciéndose en dichas superficies sendas densidades superficiales de carga de signo opuesto. Y como el conductor está descargado y aislado su carga eléctrica total <math>Q_\mathrm{C}</math> debe ser siempre nula. Por tanto, las cantidades de carga inducidas en las superficies <math>\Sigma_\mathrm{int}</math> y <math>\Sigma_\mathrm{ext}</math> debe ser opuestas: |
| - | El sistema alcanza el equilibrio cuando este campo anula al campo de la carga puntual en el interior de la región conductora <math>\tau_\mathrm{C}</math> comprendida entre las superficies esféricas <math>\Sigma_\mathrm{int}</math> y <math>\Sigma_\mathrm{ext}</math>. Es decir, | + | <center><math>Q_\mathrm{C}=\int_{\Sigma_\mathrm{int}}\!\ \!\ \sigma_e\mathrm{d}S+\int_{\Sigma_\mathrm{ext}}\!\ \!\ \sigma_e\mathrm{d}S=Q_\mathrm{int}+Q_\mathrm{ext}=0</math></center> |
| + | |||
| + | Pero, aunque la cantidad total de carga inducida es nula, al estar separada espacialmente en sendas distribuciones de signo opuesto, éstas crearán un campo eléctrico (que llamaremos “inducido”) <math>\mathbf{E}_\mathrm{ind}</math>. El sistema alcanza el equilibrio cuando este campo anula al campo de la carga puntual en el interior de la región conductora <math>\tau_\mathrm{C}</math> comprendida entre las superficies esféricas <math>\Sigma_\mathrm{int}</math> y <math>\Sigma_\mathrm{ext}</math>. Es decir, | ||
<center><math>\mathbf{E}(\mathbf{r})=\mathbf{E}_q(\mathbf{r})+\mathbf{E}_\mathrm{ind}(\mathbf{r})=\mathbf{0}\,\,\mathrm{;}\,\;\;\forall\, P\in \tau_\mathrm{C}\;\;(R_1<|\mathbf{r}|<R_2)</math></center> | <center><math>\mathbf{E}(\mathbf{r})=\mathbf{E}_q(\mathbf{r})+\mathbf{E}_\mathrm{ind}(\mathbf{r})=\mathbf{0}\,\,\mathrm{;}\,\;\;\forall\, P\in \tau_\mathrm{C}\;\;(R_1<|\mathbf{r}|<R_2)</math></center> | ||
| Línea 22: | Línea 24: | ||
===Carga eléctrica en las superficies del conductor=== | ===Carga eléctrica en las superficies del conductor=== | ||
| - | Para determinar la carga eléctrica en la superficie interior de la corteza conductora aplicamos la ley de Gauss utilizando una superficie gaussiana cerrada <math>\partial\ | + | Para determinar la carga eléctrica en la superficie interior de la corteza conductora aplicamos la ley de Gauss utilizando una superficie gaussiana cerrada <math>\partial\tau_\mathrm{a}</math> tal que todos sus puntos estén dentro de la región conductora <math>\tau_\mathrm{C}</math>. Por ejemplo, podemos tomar como <math>\partial \tau_\mathrm{a}</math> una superficie esférica con centro en <math>O</math> y radio <math>r</math>, tal que <math>R_1<r<R_2</math>. En cada punto de esta superficie el campo eléctrico total es nulo por ser punto del interior del conductor en equilibrio. Por tanto, el flujo de dicho campo y, en consecuencia, la cantidad total de carga eléctrica encerrada por <math>\partial\tau_\mathrm{a}</math>, es... |
| + | |||
| + | [[Archivo:q_en_cond_3.gif|right]]<center><math>\Phi_e\big\rfloor_{\partial\tau_\mathrm{a}}=\oint_{\partial\tau_\mathrm{a}}\!\ \mathbf{E}\cdot\mathrm{d}\mathbf{S}=0\quad\Longrightarrow\quad\Phi_e\big\rfloor_{\partial\tau_\mathrm{a}}=\frac{Q_{\partial\tau_\mathrm{a}}}{\varepsilon_0}=0</math></center> | ||
| + | |||
| + | La carga eléctrica en el interior de <math>\partial\tau_1</math> es la carga puntual <math>q</math>, más la carga distribuida en la superficie interior <math>\Sigma_\mathrm{int}</math> de la corteza conductora. Obsérvese que no hay carga eléctrica neta en el volumen de dicha corteza comprendido entre las superficies <math>\Sigma_\mathrm{int}</math> y <math>\partial\tau_\mathrm{a}</math>, ya que se trata de una región conductora en equilibrio. De esta forma, | ||
| + | |||
| + | <center><math>Q_{\partial\tau_\mathrm{a}}=q+Q_\mathrm{int}=0\quad\Longrightarrow\quad Q_\mathrm{int}=-q</math></center> | ||
| + | |||
| + | Y aplicando ahora que el conductor está descargado y aislado y que, por tanto, las cantidades de carga en sus superficies deben ser opuestas... | ||
| + | |||
| + | <center><math>Q_\mathrm{C}=Q_\mathrm{ext}+Q_\mathrm{int}=0\quad\Longrightarrow\quad Q_\mathrm{ext}=-Q_\mathrm{int}=q</math></center> | ||
| + | |||
| + | ===Campo eléctrico y potencial electrostático=== | ||
| + | ====En el exterior del sistema y en el conductor==== | ||
| + | Una vez calculada la cantidad de carga que hay en la superficie externa del conductor, pasamos a discutir cómo se distribuye. En primer lugar, hay que tener en cuenta que en el interior de la región conductora no hay campo eléctrico. Esto tiene como consecuencia que la densidad de carga eléctrica en la superficie <math>\Sigma_\mathrm{ext}</math> '''sólo está relacionada con el campo eléctrico en el exterior''': | ||
| + | |||
| + | <center><math>\mathbf{n}\cdot\bigg[\mathbf{E}(r=R_2^+)-\underbrace{\mathbf{E}(r=R_2^-)}_{=\mathbf{0}}\bigg]_{\Sigma_\mathrm{ext}}=\mathbf{n}\cdot\mathbf{E}(r=R_2^+)=\frac{\sigma_e}{\varepsilon_0}\bigg\rfloor_{\Sigma_\mathrm{ext}}</math></center> | ||
| + | |||
| + | (consecuencia de la discontinuidad del campo en la superficie cargada). Es decir, la región conductora actúa como una pantalla de manera que la carga puntual <math>q</math> y la densidad superficial de carga en la superficie interior no afectan en absoluto a la forma de distribuirse la carga en <math>\Sigma_\mathrm{ext}</math>. Y como no hay otras cargas en el exterior de dicha superficie esférica y si, además, asumimos que es homogénea, la carga eléctrica <math>Q_\mathrm{ext}=q</math> se distribuirá uniformemente, con una densidad superficial, | ||
| + | |||
| + | <center><math>\sigma_e(\mathbf{r})\big\rfloor_{\Sigma_\mathrm{ext}}=\frac{q}{4\pi\!\ R_2^2}=\sigma_2</math></center> | ||
| + | |||
| + | Obsérvese que de la discusión anterior acerca del “efecto pantalla” del conductor se deduce que el campo eléctrico resultante en el exterior de la esfera conductora depende exclusivamente de aquella distribución uniforme y esférica. Y, como sabemos, una [[Campo_eléctrico_de_esfera_cargada_en_su_superficie_GIA|distribución de carga de este tipo]] produce un campo eléctrico radial idéntico al que crearía una carga puntual <math>q</math> en el centro de la distribución (consecuencia de la aplicación de la ley de Gauss): | ||
| + | |||
| + | <center><math>\forall\, P\;\;\mathrm{tal}\;\;\mathrm{que}\quad|\mathbf{r}|=r>R_2\,\mathrm{,}\,\quad\mathbf{E}(\mathbf{r})=k_e\!\ q\ \frac{\mathbf{r}}{|\mathbf{r}|^3}=\frac{k_e\!\ q}{r^2}\ \mathbf{u}_r</math></center> | ||
| + | |||
| + | El potencial electrostático en cualquier punto <math>P</math> exterior a la corteza conductora puede calcularse como la circulación de dicho campo eléctrico, desde dicho punto hasta el infinito, o bien en términos de una integral indefinida del campo eléctrico más una constante de integración a determinar por las condiciones de contorno: | ||
| + | |||
| + | <center><math>V(P)-V(\infty)=\int_P^\infty\! \mathbf{E}\cdot\mathrm{d}\mathbf{r}\quad\longrightarrow\quad V(\mathbf{r})=C_\mathrm{ext}\ -\! \int\!\mathbf{E}\cdot\mathrm{d}\mathbf{r}=C_\mathrm{ext}\ -\ k_e\!\ q \int\frac{\mathbf{r}\cdot\mathrm{d}\mathbf{r}}{|\mathbf{r}|^3}</math></center> | ||
| + | |||
| + | Si expresamos el vector posición <math>\mathbf{r}</math> en términos del vector <math>\mathbf{u}_r</math>, y tomamos diferenciales, se tendrá que, | ||
| + | |||
| + | <center><math>\mathbf{r}=r\!\ \mathbf{u}_r\quad\Longrightarrow\quad\mathrm{d}\mathbf{r}=\mathrm{d}r\!\ \mathbf{u}_r+r\!\ \mathbf{d}\mathbf{u}_r\,\mathrm{,}\, \quad\mathrm{con}\quad\mathbf{u}_r\!\ \perp\!\ \mathrm{d}\mathbf{u}_r</math></center> | ||
| + | por ser <math>\mathbf{u}_r</math> un vector unitario. Esta condición de ortogonalidad facilita el cálculo de la expresión del potencial electrostático: | ||
| + | |||
| + | <center><math>\mathbf{r}\cdot\mathrm{d}\mathbf{r}=r\mathrm{d}r\quad\Longrightarrow\quad V(\mathbf{r})=C_\mathrm{ext}\ -\ k_e\!\ q \int\frac{\mathrm{d}r}{r^2}=\frac{k_e\!\ q}{r}=V(r)\,\mathrm{,}\,\;\;\forall\, P\;\;\mathrm{tal}\;\;\mathrm{que}\quad |\mathbf{r}|=r\geq R_2</math></center> | ||
| + | |||
| + | donde, para el valor de la constante de integración, <math>C_\mathrm{ext}=0</math>, se ha obtenido considerado que el potencial se anula en el infinito. Como puede comprobarse, la expresión obtenida es idéntica al de potencial creado por una carga puntual <math>q</math> colocada en el punto <math>O</math>. A partir de esta expresión y por continuidad del potencial, podemos determinar cuánto vale el potencial <math>V_0</math> en la superficie exterior de la corteza conductora y en cualquier punto de dicho conductor, ya que al ser el campo eléctrico nulo, el potencial será constante: | ||
| + | |||
| + | <center><math>\forall\, P\;\;\mathrm{tal}\;\;\mathrm{que}\;\;R_1\leq |\mathbf{r}|\leq R_2\,\mathrm{,}\quad V(\mathbf{r})=V_0=V(r=R_2^+)=\frac{k_e\!\ q}{R_2}</math></center> | ||
| + | |||
| + | ====En el hueco==== | ||
| + | En el enunciado no se solicita determinar el potencial en la región hueca del interior del conductor, donde se sitúa la carga puntual. Sin embargo, no es difícil determinar cómo es dicho campo escalar. Como dijimos al principio, la carga puntual crea un campo radial, pero al colocarla en el interior del hueco induce una densidad superficial de carga en la superficie interior del conductor. Ésta crea un campo inducido que, junto con el de la carga, contribuye al campo eléctrico total que hay en el hueco. Si la carga no está colocada en el centro del hueco (en el punto <math>O</math>), la densidad de carga negativa inducida será mayor cuanto más próxima se halle la carga puntual <math>q</math> y, como consecuencia, el campo eléctrico no sería radial y no podríamos hacer ninguna consideración a priori sobre su simetría. Sin embargo, como dicha carga está situada en el centro <math>O</math>, su distancia a todos los puntos de la superficie <math>\Sigma_\mathrm{int}</math> es la misma (<math>R_1</math>). Por tanto, la intensidad el campo eléctrico creado por la carga es la misma y en todos ellos induciría la misma densidad superficial de carga. En consecuencia, la carga <math>Q_\mathrm{int}=-q</math> se distribuye uniformemente en la superficie <math>\Sigma_\mathrm{int}</math>, | ||
| + | |||
| + | [[Archivo:q_en_cond_4.gif|right]]<center><math>\sigma_e(\mathbf{r})\big\rfloor_{\Sigma_\mathrm{int}}=-\frac{q}{4\pi\!\ R_1^2}=-\sigma_1</math></center> | ||
| + | |||
| + | pudiendo asegurar también que el campo eléctrico total en el hueco va a ser radial. | ||
| + | |||
| + | Apliquemos entonces la ley de Gauss tomando una superficie gaussiana <math>\partial\tau_b</math> consistente en una superficie esférica de radio <math>r<R_1</math> y centrada en O. Como la única carga encerrada en dicha superficie es la carga puntual, se tendrá: | ||
| + | |||
| + | <center><math>\Phi_e\big\rfloor_{\partial\tau_b}=\oint_{\partial\tau_b}\!\ \mathbf{E}\cdot\mathrm{d}\mathbf{S}=4\pi r^2 \!\ E(r)=\frac{q}{\varepsilon_0}\quad\Longrightarrow\quad\mathbf{E}(\mathbf{r})=k_e\!\ q\ \frac{\mathbf{r}}{|\mathbf{r}|^3}\,\mathrm{,}\,\quad\forall\, P \;\;\mathrm{tal}\;\;\mathrm{que}\quad |\mathbf{r}|<R_1</math></center> | ||
| + | |||
| + | Es decir, nuevamente obtenemos que el campo en el interior del hueco es el creado por la carga puntual <math>q</math> situada en el centro <math>O</math>. Por tanto, el potencial en dicha región deberá ser de la forma, | ||
| + | |||
| + | <center><math>V(\mathbf{r})=\frac{k_e\!\ q}{r}\ + \ C_\mathrm{int}\,\mathrm{,}\,\quad\forall\, P \;\;\mathrm{tal}\;\;\mathrm{que}\quad |\mathbf{r}|\leq R_1</math></center> | ||
| + | |||
| + | Obsérvese que para determinar el valor de la constante de integración <math>C_\mathrm{int}</math> no podemos utilizar el valor del potencial en el infinito, ya que nuestra función <math>V(r)</math> ahora sólo está definida para valores de <math>r</math> inferiores a <math>R_1</math>. Y puesto que conocemos el valor del potencial en toda la corteza conductora (incluidas sus superficies) y aquel debe ser una función continua, fijamos el valor de la constante exigiendo, | ||
| + | |||
| + | <center><math>V(r=R_1^-)=\frac{k_e\!\ q}{R_1}\ + \ C_\mathrm{int}=\frac{k_e\!\ q}{R_2}=V(r=R_1^+)\quad\Longrightarrow\quad C_\mathrm{int}=k_e\!\ q\ \left(\frac{1}{R_2}-\frac{1}{R_1}\right)</math></center> | ||
| + | |||
| + | ====Expresiones en todo el espacio==== | ||
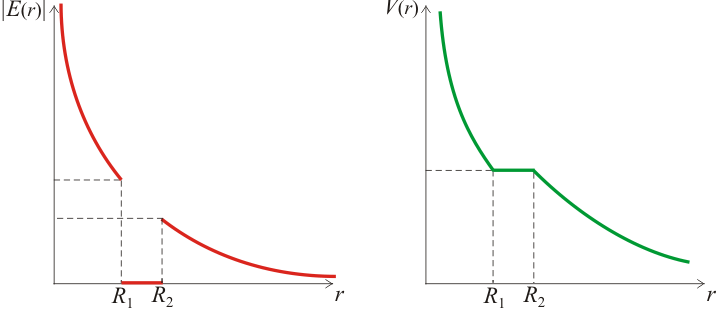
| + | En resumen, el campo eléctrico y el potencial electrostático creado por la carga puntual <math>q</math> encerrada y centrada en el conductor hueco, son de la siguiente forma: | ||
| + | |||
| + | <center><math>\mathbf{E}(\mathbf{r})=\begin{cases}\displaystyle k_e\!\ q\ \frac{\mathbf{r}}{|\mathbf{r}|^3}\,\mathrm{,}\, & R_1>|\mathbf{r}|>R_2\\ \\ \mathbf{0}\,\mathrm{,} & R_1<|\mathbf{r}|<R_2\end{cases}\quad\longleftrightarrow\quad V(\mathbf{r})=V(r)=\begin{cases}\displaystyle \frac{k_e\!\ q}{r}\,\mathrm{;}\, & r\geq R_2\\ \\ \displaystyle V_0=\frac{k_e\!\ q}{R_2}\,\mathrm{;}\, & R_1\leq r\leq R_2\\ \\ \displaystyle k_e\!\ q\ \left(\frac{1}{r}+\frac{1}{R_2}-\frac{1}{R_1}\right)\,\mathrm{;}\, & r\leq R_1\end{cases} | ||
| + | </math></center> | ||
| - | <center> | + | <center>[[Archivo:q_en_cond_5.gif]]</center> |
última version al 03:05 25 mar 2012
Contenido |
1 Enunciado
Una esfera conductora hueca de radios interior R1 y exterior R2 tiene en su centro una pequeña partícula cargada con carga q. Suponiendo que la esfera no tiene carga neta y que está aislada calcule el potencial al que se encuentra y la carga que hay en sus superficies interior y exterior.2 Solución
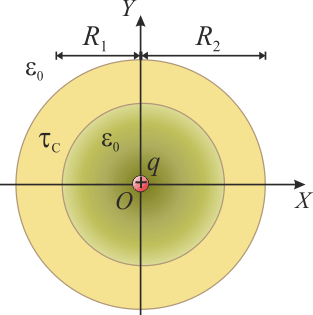
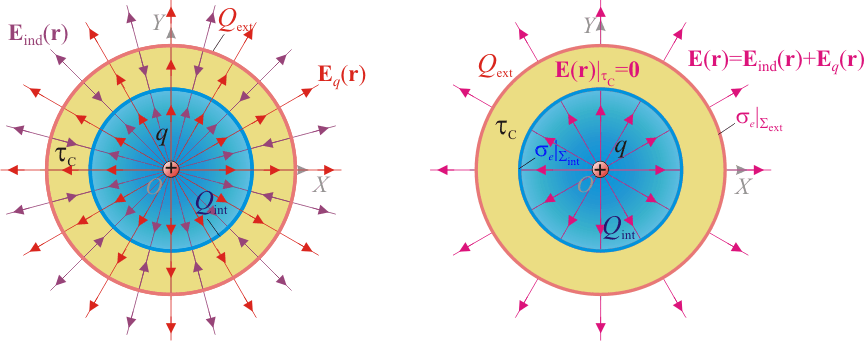
En la figura se muestra una sección transversal del sistema bajo estudio. Se trata de una esfera conductora de radio R2, descargada y aislada, en cuyo interior hay un hueco esférico y concéntrico de radio R1, que se encuentra vacío salvo en su centro O, donde hay situada una carga puntual de valor q. Ésta carga produce una campo eléctrico radial con centro en la carga (es decir, en el punto O),
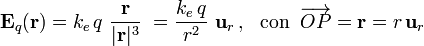
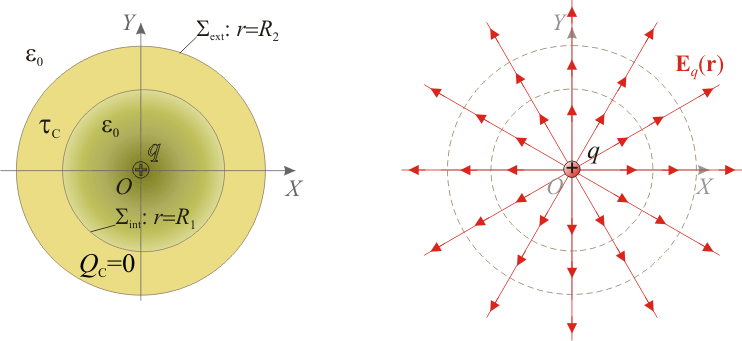
definido en todos los puntos del espacio. Si la carga puntual, que supondremos positiva, se encuentra en el hueco de la esfera conductora, este campo eléctrico arrastrará las cargas libres negativas del conductor hacia la superficie interior 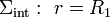 , a la vez que desplazaría las posibles cargas libres positivas hacia la exterior,
, a la vez que desplazaría las posibles cargas libres positivas hacia la exterior, 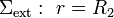 , induciéndose en dichas superficies sendas densidades superficiales de carga de signo opuesto. Y como el conductor está descargado y aislado su carga eléctrica total QC debe ser siempre nula. Por tanto, las cantidades de carga inducidas en las superficies Σint y Σext debe ser opuestas:
, induciéndose en dichas superficies sendas densidades superficiales de carga de signo opuesto. Y como el conductor está descargado y aislado su carga eléctrica total QC debe ser siempre nula. Por tanto, las cantidades de carga inducidas en las superficies Σint y Σext debe ser opuestas:
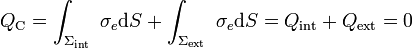
Pero, aunque la cantidad total de carga inducida es nula, al estar separada espacialmente en sendas distribuciones de signo opuesto, éstas crearán un campo eléctrico (que llamaremos “inducido”) 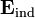 . El sistema alcanza el equilibrio cuando este campo anula al campo de la carga puntual en el interior de la región conductora τC comprendida entre las superficies esféricas Σint y Σext. Es decir,
. El sistema alcanza el equilibrio cuando este campo anula al campo de la carga puntual en el interior de la región conductora τC comprendida entre las superficies esféricas Σint y Σext. Es decir,
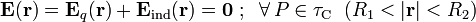
2.1 Carga eléctrica en las superficies del conductor
Para determinar la carga eléctrica en la superficie interior de la corteza conductora aplicamos la ley de Gauss utilizando una superficie gaussiana cerrada 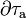 tal que todos sus puntos estén dentro de la región conductora τC. Por ejemplo, podemos tomar como
tal que todos sus puntos estén dentro de la región conductora τC. Por ejemplo, podemos tomar como 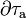 una superficie esférica con centro en O y radio r, tal que R1 < r < R2. En cada punto de esta superficie el campo eléctrico total es nulo por ser punto del interior del conductor en equilibrio. Por tanto, el flujo de dicho campo y, en consecuencia, la cantidad total de carga eléctrica encerrada por
una superficie esférica con centro en O y radio r, tal que R1 < r < R2. En cada punto de esta superficie el campo eléctrico total es nulo por ser punto del interior del conductor en equilibrio. Por tanto, el flujo de dicho campo y, en consecuencia, la cantidad total de carga eléctrica encerrada por 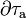 , es...
, es...
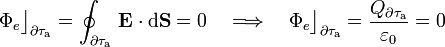
La carga eléctrica en el interior de 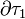 es la carga puntual q, más la carga distribuida en la superficie interior Σint de la corteza conductora. Obsérvese que no hay carga eléctrica neta en el volumen de dicha corteza comprendido entre las superficies Σint y
es la carga puntual q, más la carga distribuida en la superficie interior Σint de la corteza conductora. Obsérvese que no hay carga eléctrica neta en el volumen de dicha corteza comprendido entre las superficies Σint y 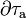 , ya que se trata de una región conductora en equilibrio. De esta forma,
, ya que se trata de una región conductora en equilibrio. De esta forma,
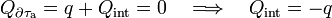
Y aplicando ahora que el conductor está descargado y aislado y que, por tanto, las cantidades de carga en sus superficies deben ser opuestas...
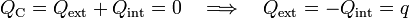
2.2 Campo eléctrico y potencial electrostático
2.2.1 En el exterior del sistema y en el conductor
Una vez calculada la cantidad de carga que hay en la superficie externa del conductor, pasamos a discutir cómo se distribuye. En primer lugar, hay que tener en cuenta que en el interior de la región conductora no hay campo eléctrico. Esto tiene como consecuencia que la densidad de carga eléctrica en la superficie Σext sólo está relacionada con el campo eléctrico en el exterior:
![\mathbf{n}\cdot\bigg[\mathbf{E}(r=R_2^+)-\underbrace{\mathbf{E}(r=R_2^-)}_{=\mathbf{0}}\bigg]_{\Sigma_\mathrm{ext}}=\mathbf{n}\cdot\mathbf{E}(r=R_2^+)=\frac{\sigma_e}{\varepsilon_0}\bigg\rfloor_{\Sigma_\mathrm{ext}}](/wiki/images/math/5/b/6/5b67e830b765752f7512b78ba570d2ae.png)
(consecuencia de la discontinuidad del campo en la superficie cargada). Es decir, la región conductora actúa como una pantalla de manera que la carga puntual q y la densidad superficial de carga en la superficie interior no afectan en absoluto a la forma de distribuirse la carga en Σext. Y como no hay otras cargas en el exterior de dicha superficie esférica y si, además, asumimos que es homogénea, la carga eléctrica Qext = q se distribuirá uniformemente, con una densidad superficial,
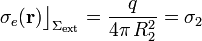
Obsérvese que de la discusión anterior acerca del “efecto pantalla” del conductor se deduce que el campo eléctrico resultante en el exterior de la esfera conductora depende exclusivamente de aquella distribución uniforme y esférica. Y, como sabemos, una distribución de carga de este tipo produce un campo eléctrico radial idéntico al que crearía una carga puntual q en el centro de la distribución (consecuencia de la aplicación de la ley de Gauss):
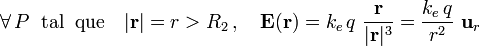
El potencial electrostático en cualquier punto P exterior a la corteza conductora puede calcularse como la circulación de dicho campo eléctrico, desde dicho punto hasta el infinito, o bien en términos de una integral indefinida del campo eléctrico más una constante de integración a determinar por las condiciones de contorno:
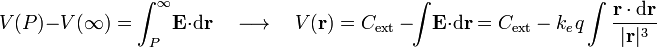
Si expresamos el vector posición  en términos del vector
en términos del vector 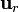 , y tomamos diferenciales, se tendrá que,
, y tomamos diferenciales, se tendrá que,
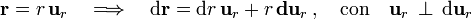
por ser 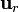 un vector unitario. Esta condición de ortogonalidad facilita el cálculo de la expresión del potencial electrostático:
un vector unitario. Esta condición de ortogonalidad facilita el cálculo de la expresión del potencial electrostático:
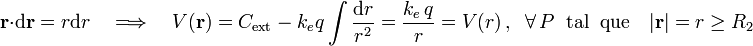
donde, para el valor de la constante de integración, Cext = 0, se ha obtenido considerado que el potencial se anula en el infinito. Como puede comprobarse, la expresión obtenida es idéntica al de potencial creado por una carga puntual q colocada en el punto O. A partir de esta expresión y por continuidad del potencial, podemos determinar cuánto vale el potencial V0 en la superficie exterior de la corteza conductora y en cualquier punto de dicho conductor, ya que al ser el campo eléctrico nulo, el potencial será constante:
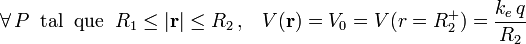
2.2.2 En el hueco
En el enunciado no se solicita determinar el potencial en la región hueca del interior del conductor, donde se sitúa la carga puntual. Sin embargo, no es difícil determinar cómo es dicho campo escalar. Como dijimos al principio, la carga puntual crea un campo radial, pero al colocarla en el interior del hueco induce una densidad superficial de carga en la superficie interior del conductor. Ésta crea un campo inducido que, junto con el de la carga, contribuye al campo eléctrico total que hay en el hueco. Si la carga no está colocada en el centro del hueco (en el punto O), la densidad de carga negativa inducida será mayor cuanto más próxima se halle la carga puntual q y, como consecuencia, el campo eléctrico no sería radial y no podríamos hacer ninguna consideración a priori sobre su simetría. Sin embargo, como dicha carga está situada en el centro O, su distancia a todos los puntos de la superficie Σint es la misma (R1). Por tanto, la intensidad el campo eléctrico creado por la carga es la misma y en todos ellos induciría la misma densidad superficial de carga. En consecuencia, la carga Qint = − q se distribuye uniformemente en la superficie Σint,
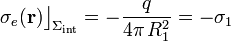
pudiendo asegurar también que el campo eléctrico total en el hueco va a ser radial.
Apliquemos entonces la ley de Gauss tomando una superficie gaussiana 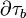 consistente en una superficie esférica de radio r < R1 y centrada en O. Como la única carga encerrada en dicha superficie es la carga puntual, se tendrá:
consistente en una superficie esférica de radio r < R1 y centrada en O. Como la única carga encerrada en dicha superficie es la carga puntual, se tendrá:
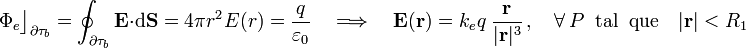
Es decir, nuevamente obtenemos que el campo en el interior del hueco es el creado por la carga puntual q situada en el centro O. Por tanto, el potencial en dicha región deberá ser de la forma,
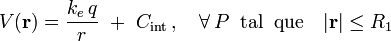
Obsérvese que para determinar el valor de la constante de integración Cint no podemos utilizar el valor del potencial en el infinito, ya que nuestra función V(r) ahora sólo está definida para valores de r inferiores a R1. Y puesto que conocemos el valor del potencial en toda la corteza conductora (incluidas sus superficies) y aquel debe ser una función continua, fijamos el valor de la constante exigiendo,
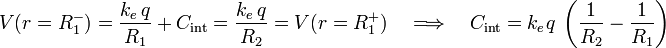
2.2.3 Expresiones en todo el espacio
En resumen, el campo eléctrico y el potencial electrostático creado por la carga puntual q encerrada y centrada en el conductor hueco, son de la siguiente forma: