Producción de entropía por descompresión
De Laplace
| Línea 6: | Línea 6: | ||
Calcule la posición final del émbolo, una vez que se alcanza de nuevo el equilibrio, la temperatura final del aire y la variación de entropía en el proceso. Halle la variación en la exergía del gas en el proceso. | Calcule la posición final del émbolo, una vez que se alcanza de nuevo el equilibrio, la temperatura final del aire y la variación de entropía en el proceso. Halle la variación en la exergía del gas en el proceso. | ||
==Temperatura y volumen== | ==Temperatura y volumen== | ||
| + | Inicialmente tenemos el gas a una presión <math>p_1</math>, ocupando un volumen <math>V_1</math> y con una temperatura <math>T_1=T_0</math> siendo <math>T_0</math> la temperatura exterior. Una vez que se libera el pistón el gas se expande debido a la diferencia de presiones. El estado final se caracteriza porque <math>p_2=p_0</math>, siendo <math>p_0</math> la presión exterior. El volumen final será <math>V_2</math>. La temperatura final <math>T_2</math> no tiene por qué coincidir con la inicial, pues al estar el recipiente aislado térmicamente no se alcanza el equilibrio térmico con el exterior. | ||
| + | |||
| + | Se cumple la relación | ||
| + | |||
| + | <center><math>T_1=T_0\qquad\qquad p_2=p_0\qquad\qquad \frac{p_1V_1}{T_0}=\frac{p_0V_2}{T_2}</math></center> | ||
| + | |||
| + | Obtenemos el estado final aplicando el primer principio de la termodinámica. | ||
| + | |||
| + | La presión exterior es en todo momento la atmosférica, por lo que el trabajo realizado sobre el gas vale | ||
| + | |||
| + | <center><math>W = -\int_{V_1}^{V_2}p_\mathrm{ext}\,\mathrm{d}V=-p_0(V_2-V_1)</math></center> | ||
| + | |||
| + | Este trabajo será negativo, pues en realidad es el gas el que lo realiza. | ||
| + | |||
| + | Al ser las paredes adiabáticas, no existe transferencia de calor con el exterior y el calor que entra en el sistema es nulo | ||
| + | |||
| + | <center><math>Q=0\,</math></center> | ||
| + | |||
| + | Por tanto, el trabajo realizado sobre el sistema corresponde a una variación de su energía interna | ||
| + | |||
| + | <center><math>\Delta U = nc_v(T_2-T_0)\,</math></center> | ||
| + | |||
| + | cumpliéndose | ||
| + | |||
| + | <center><math>\overbrace{Q}^{=0}+W = \Delta U \qquad\Rightarrow\qquad -p_0(V_2-V_0) = nc_v(T_2-T_0)</math></center> | ||
| + | |||
| + | En este caso, el trabajo que realiza | ||
==Entropía== | ==Entropía== | ||
==Exergía== | ==Exergía== | ||
[[Categoría:Problemas del segundo principio de la termodinámica (GIE)]] | [[Categoría:Problemas del segundo principio de la termodinámica (GIE)]] | ||
Revisión de 20:53 23 mar 2012
Contenido |
1 Enunciado
Se tiene un cilindro de 20 cm de diámetro tapado por un émbolo situado inicialmente a 15 cm del fondo. En el interior del émbolo se encuentra aire comprimido a 4.0 bares, siendo la presión exterior 100 kPa. La temperatura exterior y la inicial del aire son 300 K. Las paredes del cilindro y el pistón son completramente adiabáticos.
Inicialmente, el pistón está sujeto por un perno, que se libera bruscamente, produciéndose una expansión abrupta.
Calcule la posición final del émbolo, una vez que se alcanza de nuevo el equilibrio, la temperatura final del aire y la variación de entropía en el proceso. Halle la variación en la exergía del gas en el proceso.
2 Temperatura y volumen
Inicialmente tenemos el gas a una presión p1, ocupando un volumen V1 y con una temperatura T1 = T0 siendo T0 la temperatura exterior. Una vez que se libera el pistón el gas se expande debido a la diferencia de presiones. El estado final se caracteriza porque p2 = p0, siendo p0 la presión exterior. El volumen final será V2. La temperatura final T2 no tiene por qué coincidir con la inicial, pues al estar el recipiente aislado térmicamente no se alcanza el equilibrio térmico con el exterior.
Se cumple la relación
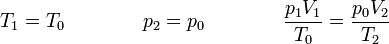
Obtenemos el estado final aplicando el primer principio de la termodinámica.
La presión exterior es en todo momento la atmosférica, por lo que el trabajo realizado sobre el gas vale

Este trabajo será negativo, pues en realidad es el gas el que lo realiza.
Al ser las paredes adiabáticas, no existe transferencia de calor con el exterior y el calor que entra en el sistema es nulo
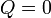
Por tanto, el trabajo realizado sobre el sistema corresponde a una variación de su energía interna
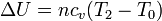
cumpliéndose

En este caso, el trabajo que realiza





